 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Энтропия сложной системы
На практике часто приходится определять энтропию для сложной системы, полученной объединением двух или более простых систем. Под объединением двух систем Очевидно, число возможных состояний системы
Вероятности
Найдем энтропию сложной системы. По определению она равна сумме произведений вероятностей всех возможных ее состояний на их логарифмы с обратным знаком:
или, в других обозначениях:
Энтропию сложной системы, как и энтропию простой, тоже можно записать в форме математического ожидания:
где Аксиома 1. Количество информации в любой подсистеме иерархической системы определяется произведением количества сигналов, исходящих от подсистемы нулевого уровня (исходной вершины) и достигающих данную подсистему (или входящих в данную подсистему), и энтропии этих сигналов. Аксиома 2. Энтропия любого элемента управляющей подсистемы при переходе в новое целевое состояние (при смене цели) определяется исходным (от нулевого уровня) информационным потоком и энтропией этого элемента. Аксиома 3. Энтропия всей управляющей подсистемы при переходе в новое целевое состояние определяется суммой (точнее интегральной оценкой) энтропии всех её элементов. Аксиома 4. Полный информационный поток, направленный на объект управления за период его перехода в новое целевое состояние, равен разности энтропии всей управляющей подсистемы при переходе в новое целевое состояние и энергии объекта управления, затрачиваемой объектом управления на переход в новое состояние. Аксиома 5. Информационная работа управляющей подсистемы по преобразованию ресурсов состоит из двух частей: работы управляющей подсистемы, затраченной на компенсацию исходной энтропии, и работы, направленной на управляемый объект, т.е. на удерживание системы в устойчивом состоянии. Аксиома 6. Полезная работа управляющей подсистемы в течении некоторого промежутка времени должна соответствовать полному информационному потоку, воздействующему на управляемую систему (в соответствии с аксиомой 4) за рассматриваемый период времени.
Поиск по сайту: |
 и
и  с возможными состояниями
с возможными состояниями  понимается сложная система
понимается сложная система  , состояния которой
, состояния которой  представляют собой все возможные комбинации состояний
представляют собой все возможные комбинации состояний  систем
систем 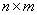 . Обозначим
. Обозначим  вероятность того, что система
вероятность того, что система  . (18.3.1)
. (18.3.1)



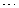
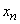










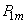

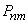
 (18.3.2)
(18.3.2) . (18.3.2')
. (18.3.2') , (18.3.3)
, (18.3.3)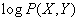 - логарифм вероятности состояния системы, рассматриваемый как случайная величина (функция состояния).
- логарифм вероятности состояния системы, рассматриваемый как случайная величина (функция состояния).