Полный одноразрядный двоичный сумматор

Он (рис. 4) имеет три входа: a, b для двух слагаемых и p для переноса из предыдущего (более младшего) разряда и два выхода: S сумма, P перенос в следующий (более старший) разряд. Обозначением полного двоичного сумматора служат буквы SM. Работу его отражает таблица истинности 3 (табл. 3).

Рис. 4

Таблица 3 № наб. a b p P S

Отметим два момента. Первый: в табл. 2 и 3 выходные сигналы P и S не случайно расположены именно в такой последовательности. Это подчеркивает, что PS рассматривается как двухразрядное двоичное число, например, 1 + 1 = 2₁₀ = 10₂ , то есть P = 1, а S = 0 или 1 + 1 + 1 = 3₁₀ = 11₂, то есть P = 1, а S = 1. Второй: выходные сигналы P и S полного двоичного сумматора относятся к классу самодвойственных функций алгебры логики. Самодвойственными называют функции, инвертирующие свое значение при инвертировании всех переменных, от которых они зависят. Обратите внимание, что P и S для четвертьсумматора и полусумматора не являются самодвойственными функциями! Преимущества, вытекающие из этого свойства полного двоичного сумматора, будут рассмотрены при анализе возможностей ИС типа 155ИМ1.

Уравнения, описывающие работу полного двоичного сумматора, представленные в совершенной дизъюнктивной нормальной форме (СДНФ), имеют вид:

(6)

Уравнение для переноса может быть минимизировано:

P = ab + ap + bp. (7)

При практическом проектированиии сумматора уравнения (6) и (7) могут быть преобразованы к виду, удобному для реализации на заданных логических элементах с некоторыми ограничениями (по числу логических входов и др.) и удовлетворяющему предъявляемым к сумматору требованиям по быстродействию.

Например, преобразуем уравнения (6) следующим образом:

(8)

Из выражений (8) следует, что полный двоичный сумматор может быть реализован на двух полусумматорах и одном двухвходовом элементе ИЛИ. Соответствующая схема приведена на рис. 5.

Рис. 5

Из выражения (8) для S также следует:

S = a Å b Å p. (9)

Примечание. Так как операция Е в выражении (9) коммутативна (переменные можно менять местами), то следует, что три входа полного двоичного сумматора абсолютно равноправны и на любой из них можно подавать любую входную переменную. Это полезно помнить, разводя печатные платы, на которых установлены ИС сумматоров.

К настоящему времени разработано большое число схем сумматоров. Доказано (нашим отечественным ученым Вайнштейном), что при использовании только одного инвертора нельзя реализовать полный двоичный сумматор со сложностью P_кв < 16, а при двух инверторах P_кв < 14, где P_кв вес по Квайну, используемый как оценка сложности любых комбинационных схем. Pкв это общее число всех входов всех логических элементов схемы без учета инверторов.

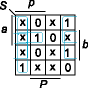
Рис. 6

Покажем, используя два метода, как была получена рациональная (с использованием только одного инвертора) схема полного двоичного сумматора, явившаяся основой схем ИС сумматоров типа 7480, 155ИМ1 и др.

Первый метод основан на использовании значения выходного переноса P как вспомогательной переменной при определении выходной суммы S (табл. 4). В табл. 4 при наборах переменных, являющихся нереальными (например, единичное значение переноса при нулевых значениях всех входных переменных), поставлены безразличные значения (крестик) для функции S, которые можно доопределять произвольным образом.

Таблица 4

Из карты Карно для функции S (рис. 6) следует:
S = abp + Pa + Pb + Pp = = abp + P(a + b + p). (10)

Второй метод основан на применении диаграмм Венна. На рис. 7а показана диаграмма Венна для трех переменных а, b, p; области, ограниченные окружностями, соответствуют переменным а, b, p, а области, обозначенные цифрами от 0 до 7 соответствующим конъюнкциям (например, 5 = abp). Область, заштрихованная на рис. 7б, очевидно, соответствует функции P = ab + ap + bp. Функция S представлена заштрихованной областью на рис. 7в. Ее можно представить суммой произведения функции a + b + p (рис. 7г) на функцию ab + ap + bp (рис. 7д) и функции abp (рис. 7е). Очевидно, что в этом случае получается выражение для S, аналогичное уравнению (10).

Рис. 7

Схема сумматора, реализованного по уравнениям (7) и (10), приведена на рис. 8а. В данной схеме используются многовходовые логические элементы И и ИЛИ. Если использовать только двухвходовые элементы, то получаются схемы, приведенные на рис. 8б,в.

Рис. 8

Поиск по сайту: