 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Формулы преобразования координат. Поворотные матрицы
Для любой точки М тела с координатами x, y, z в подвижной системе координат Оxyz, жестко связанной с ним, и с ее же координатами X, Y, Z в неподвижной системе координат ОXYZ в соответствии с (3.10), взаимосвязь проекций вектора точки
или где Переход от осей системы[X]н к осям системы [x1] осуществляется поворотом на угол прецессии ψвокруг неподвижной OY – оси прецессии системы [X]н (рис. 3.9 … 3.11). Переход от осей системы[x1] к осям системы[x2] осуществляется поворотом на уголнутацииθ вокруг оси
Рис. 3.9
Переход от осей системы [x2] к осям системы[x]п– поворотом на уголротации (собственного вращения ) φвокруг оси
а б в
Рис. 3.10
Формулы преобразования координат получаем, рассмотрев переход от системы ОXYZ ([X]н) к системе Оxyz ([x]п), выполненный с помощью трех поворотов: 1. Поворота системы ОXYZ вокруг второй из координатных осей ОY на угол прецессии ψ, т.е. [X]н®[x1], ОXYZ ® X = x1 cos y + 0 + z1 sin y , Y = 0 + y1 + 0 , Z = - x1 sin y + 0 + z1 cos y , или в матричной форме [X] ={a2y} т [x1], (3.16) где поворотная матрица {a2y} т = описывает поворот вокруг второй оси ОY на угол прецессии ψ .
а б
Рис. 3.11
2. Поворота системы Формулы преобразования координат, как видно из рис. 3.11,б, при этом таковы: x1 = x2 cos q - y2 sin q + 0, y1 = x2 sin q + y2 cos q + 0, z1 = 0 + 0 + z 2, или в матричной форме [x1] = {a3q } т [x2], (3.18) где матрица {a3q } т = описывает поворот вокруг оси 0z1 на угол нутации q. 3. Поворота системы x(2) = x cos j + 0 + z sin j , y(2) = 0 + y + 0 , z(2) = - x sin j + 0 + z cos j , или в матричной форме [x2 ] = { a2j }т [x], (3.20) поворотная матрица { a2j }т аналогична (3.17) {a2y} т: {a2φ} т = Подставляя в (3.16) соотношение (3.18), получаем промежуточную формулу преобразования координат, которая может понадобиться в дальнейшем [X] ={a2y} т {a3q} т [x(2)] , (3.22) где промежуточная поворотная матрица {a2y,3q }т находится как произведение двух матриц поворота, { a2y,3q }т = { a2y}т {a3q } т = = = Подставим в (3.16) формулы (3.18) и (3.20): [X] ={a2y} т {a3q} т {a2j }т [x]. (3.24) Сравнивая выражения (3.15) и (3.24), находим, что искомая поворотная матрица {ay,q,j } т = =
При заданном законе сферического движения выражения (3.15) и (3.25) позволяют определить искомый закон движения и траекторию выбранной точки твердого тела. 3.4. Мгновенная угловая скорость и угловое ускорение. Твердое тело с одной неподвижной точкой в общем случае участвует одновременно в трех вращениях, векторы угловых скоростей которых с использованием углов Эйлера имеют вид:
Здесь
Рис. 3.12
Ось, совпадающая с вектором Мгновенная угловая скорость меняется с течением времени как по величине, так и по направлению. Это изменение определяетсяпроизводной по времени от угловой скорости и называется мгновенным угловым ускорением
или
Рис. 3.13
Алгебраические величины проекций
Согласно (3.26),
Разложение единичного вектора
Единичный вектор
Подставляя (3.29) , (3.30) в соотношение (3.26), получаем
Таким образом, искомые проекции вектора угловой скорости на оси подвижной (связанной с телом) системы координат будут равны
Полученные соотношения носят название кинематических уравнений Эйлера. Они устанавливают связь между проекциями вектора угловой скорости тела
Поиск по сайту: |
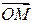 на оси двух систем координат [X]н и [x]п имеет вид
на оси двух систем координат [X]н и [x]п имеет вид , (3.14)
, (3.14)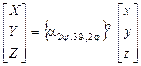 , (3.15)
, (3.15) ,
,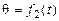 ,
,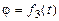 -углы Эйлера;
-углы Эйлера; 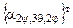 - матрица, транспонированная к матрице направляющих косинусов
- матрица, транспонированная к матрице направляющих косинусов 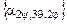 ,задающей преобразование поворота от осей неподвижной системы OXYZ (с базисом [X]н)к осям подвижной системы Оxyz (с базисом [x]п ), неизменно связанной с телом. Транспонированная матрица
,задающей преобразование поворота от осей неподвижной системы OXYZ (с базисом [X]н)к осям подвижной системы Оxyz (с базисом [x]п ), неизменно связанной с телом. Транспонированная матрица  системы [x1] (рис. 3.5 … 3.11,б).
системы [x1] (рис. 3.5 … 3.11,б).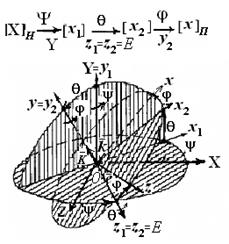
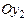 системы[x2] .
системы[x2] .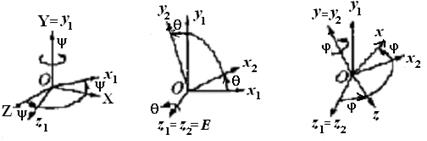
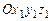 , причем
, причем 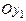
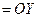 (рис. 3.9 … 3.11,а). Координаты систем координат ОXYZ и
(рис. 3.9 … 3.11,а). Координаты систем координат ОXYZ и 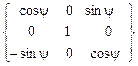 (3.17)
(3.17)
 , при этом
, при этом  (рис. 3.7,3.9, 3.11,б).
(рис. 3.7,3.9, 3.11,б).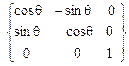 (3.19)
(3.19) на уголротации (собственного вращения ) φ,т.е.[x2]®[x]п(рис. 3.7, 3.9 … 3.11,а),
на уголротации (собственного вращения ) φ,т.е.[x2]®[x]п(рис. 3.7, 3.9 … 3.11,а), 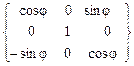 . (3.21)
. (3.21)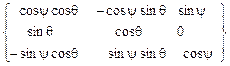 .
.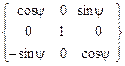
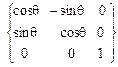
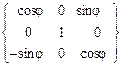 =(3.25)
=(3.25)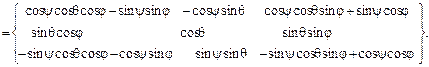
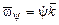 –вектор угловой скорости прецессии;
–вектор угловой скорости прецессии;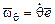 – вектор угловой скорости нутации;
– вектор угловой скорости нутации; – вектор угловой скорости ротации (собственного вращения).
– вектор угловой скорости ротации (собственного вращения).  – единичные орты осей вращения OY, OE, Oy соответственно (рис. 3.8, 3.12). Поскольку названные оси пересекаются в точке О,тоабсолютное движение тела в каждый момент времени есть вращение вокруг мгновенной оси, проходящей через точку пересечения вышеназванных осей с мгновенной угловой скоростью
– единичные орты осей вращения OY, OE, Oy соответственно (рис. 3.8, 3.12). Поскольку названные оси пересекаются в точке О,тоабсолютное движение тела в каждый момент времени есть вращение вокруг мгновенной оси, проходящей через точку пересечения вышеназванных осей с мгновенной угловой скоростью 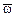 , равной геометрической сумме векторов угловых скоростей составляющих:
, равной геометрической сумме векторов угловых скоростей составляющих: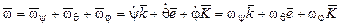 . (3.26)
. (3.26)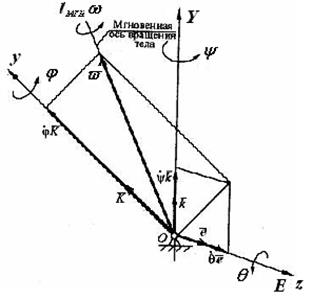
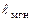 твердого тела вокруг неподвижной точки О. Мгновенная ось вращения представляет собой геометрическое место точек тела, скорости которых в данный момент времени равны нулю.
твердого тела вокруг неподвижной точки О. Мгновенная ось вращения представляет собой геометрическое место точек тела, скорости которых в данный момент времени равны нулю.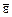 тела:
тела: , (3.27)
, (3.27)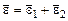 , где
, где 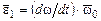 – составляющая
– составляющая 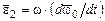 – составляющая
– составляющая 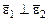 ). Вектор мгновенного углового ускорения
). Вектор мгновенного углового ускорения 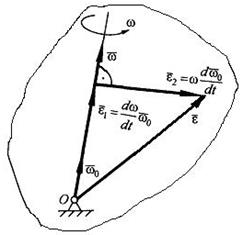
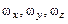 вектора
вектора  соответственно,
соответственно,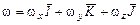 . (3.28)
. (3.28)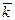 по базису [x]п, как следует из формул (3.15) и (3.25), таково:
по базису [x]п, как следует из формул (3.15) и (3.25), таково: . (3.29)
. (3.29)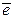 , как следует из (3.20) и (3.21), можно представить в виде
, как следует из (3.20) и (3.21), можно представить в виде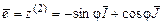 . (3.30)
. (3.30)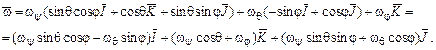
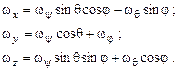 или
или  (3.31)
(3.31)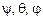 и их первыми производными по времени.
и их первыми производными по времени.