 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Учет многополосности движения на проезжей части при загружении поперечной линии влияния нагрузки
Если на проезжей части устанавливается несколько полос нагрузки АК, то самую неблагоприятную из них принимают полностью, а для остальных полос вводится уменьшающий коэффициент S1=0,6 к равномерно распределенной нагрузке. Он учитывает вероятность одновременного полного загружения автомобилями всех полос. Нагрузка на тележки при этом остается без изменения.
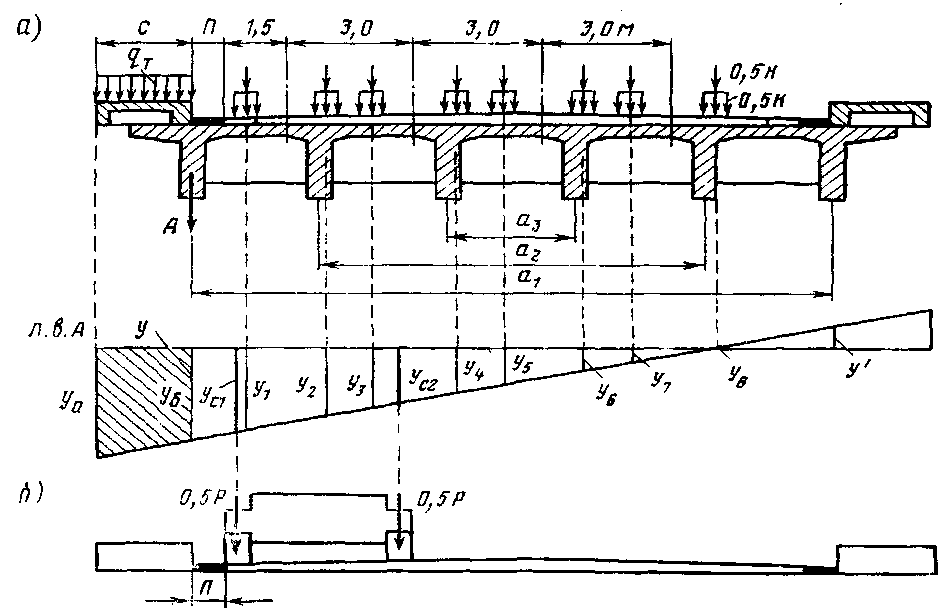
Расчетные формулы для вычисления коэффициента поперечной установки ( с учетом приведенного ниже рисунка-1 схемы загружения)
От тротуарной нагрузки
Нагрузка принята только на один тротуар, так как загружение другого тротуара способствовало бы уменьшению расчетного силового фактора для рассматриваемой крайней балки.
От равномерно распределенной нагрузки АК
от тележек АК
от одиночной нагрузки типа НК-80
№27 . Расчетные формулы для изгибающих моментов и поперечных сил в сечениях балок неразрезных пролетных строений с учетом их пространственной работы под воздействием постоянной и временной нагрузок.
От нагрузки типа АК и собственного веса пролетного строения
где q - расчетная нагрузка от собственного веса 1 м рассчитываемой балки с учетом веса балки и одежды ездового полотна с разными коэффициентами надежности по нагрузке для балки, выравнивающего, защитного, и изоляционного слоев и покрытия; qt,v - интенсивность равномерно - распределенной нагрузки от толпы на тротуарах и от автомобильной нагрузки типа АК, у f~ соответствующие коэффициенты надежности по нагрузке , ω-соответствующая площадь линии влияния расчетного силового фактора, Р- нагрузка на ось тележки от АК, y1 ,y2 – соответствующие ординаты линий влияния М и Q под грузами Р. η - коэффициенты поперечной установки, вычисляемые при загружении линии влияния нагрузки на балку. (1 + μ) - динамический коэффициент, вычисляемый по формуле (23) СНиП 2.05.03-84* (1 + μ) = Здесь λ- сумма длин загружаемых участков линии влияния ( вместе с разделяющими их участками).
№28 : Расчет прочности нормальных сечений предварительно Напряженных балок. Предварительно напряженные балки при ограничении трещинообразования под воздействием временной и постоянной нагрузок можно рассчитывать в предположении упругой работы материала. Вспомним вначале основную идею предварительного натяжения. Она состоит в создании до приложения эксплуатационной нагрузки обжатия в бетоне там, где в результате её воздействия возникнут растягивающие напряжения. Благодаря этому в растянутой зоне бетона должны быть преодолены эти предварительно сжимающие напряжения раньше, чем возникнет действительное растяжение. Чтобы пояснить это рассмотрим ход первых простейших опытов по предварительному напряжению (рис. 11. 1,а).
Рис.11.1.К основной идее предварительного натяжения: а -центральное обжатие бетонной призмы; b-центрально обжатая призма на опорах; с- компоненты напряжения в бетоне от обжатия и поперечной нагрузки когда растягивающие напряжения от поперечной нагрузки меньше напряжений обжатия; d- тоже, но растягивающие напряжения от поперечной нагрузки больше напряжений обжатия.
В бетонную призму заложим центрально стальной стержень, снабженный на концах анкерными плитками, резьбой и гайками; после затвердения бетона стержень можно растянуть при помощи гаек. Первоначальная длина стержня равна расстоянию l' между внутренними плоскостями гаек. Первоначальная длина бетонной призмы равна расстоянию l между внутренними плоскостями анкерных плиток. Примем, что стержень может скользить в бетоне; тогда он по всей своей длине подвергнется удлинению в соответствии с напряжением. Вызванная натяжением стержня растягивающая сила приложена через гайки и опорные или анкерные плитки к бетону и вызывает в нем напряжения сжатия. Бетон при этом укорачивается, а размеры концевых участков стального стержня, выступающих из бетонной призмы, возрастут как за счет удлинения стержня, так и за счет укорочения бетона. При этом измеренное общее перемещение концов стрежня относительно бетонной призмы состоит из удлинения стали Усилие растяжения в стальном стержне есть предварительное натяжение V, которое действует на бетонный элемент в виде внешней силы, находящейся в равновесии. Стальной стержень был расположен центрально и таким образом создавал в бетоне равномерное сжимающее напряжение. Если теперь поместить эту предварительно напряженную железобетонную призму (рис.11.1,Б), то в ней возникнут изгибающие моменты, вызывающие равные сжимающие и растягивающие напряжения σbz, накладывающиеся на предварительные напряжения σbv При этом сжимающие напряжения, вызванные предварительным напряжением, в сжатом поясе увеличатся, а в растянутом поясе — уменьшатся; в бетоне не будут возникать растягивающие напряжения, пока напряжения изгиба будут оставаться меньше предварительных напряжений сжатия.(рис.11.,1,с). Когда напряжения от изгиба превзойдут предварительные сжимающие напряжения(рис.11.1,<1) то возникнут действительные растягивающие напряжения, и при дальнейшем повышении нагрузки после преодоления сопротивления бетона растяжению образуются трещины, как в обычном железобетоне. При этом рабочее сечение внезапно изменится и вместо сплошного прямоугольного оно преобразится в небольшую сжатую зону. Кроме того в сечении при этом будет действовать еще растягивающая сила в стальном стержне, если не учитывать сопротивление бетона растяжению. Если учесть, что сжимающие напряжения бетона имеют верхний предел, определяемый его расчетным сопротивлением то станет ясно, что предварительные напряжения сжатия при изгибе уменьшают несущую способность сжатой зоны; в то же время в растянутой зоне сжимающие напряжения полностью используются как напряжения, снимаемые впоследствии напряжениями от нагрузки, и потому желательны. Таким образом, центральное приложение силы натяжения для создания предварительного напряжения при изгибе недостаточно целесообразно, так как при этом не удается полностью использовать возможности верхней зоны на сжатие. Поэтому лучше поместить натягиваемый стержень внецентренно, как показано на рис. 11.2.,а, в нижней крайней точке ядра сечения( при прямоугольном сечении — на!/3 высоты); при этом в результате одного только предварительного напряжения получаем треугольную эпюру сжимающих напряжений, на которую накладываются напряжения от изгиба под воздействием внешней нагрузки. При этом удается использовать расчетные сопротивления бетона сжатию как при создании предварительного напряжения (внизу), так и при изгибе (вверху).
Рис.11.2.Стержень арматуры расположен в нижней точке ядра сечения(а) и ниже его(b).
Если имеется постоянная нагрузка, то можно натягиваемый стержень расположить ниже ядра сечения и допустить возникновение растягивающего напряжения в верхней зоне балки от силы натяжения стержня. Это растягивающее напряжение может быть доведено до величины, равной сжимающему напряжению, возникающему в верхней зоне от изгиба под постоянной нагрузкой (рис. 1.1.2, b). Так как момент Мg от постоянной нагрузки над опорой равен нулю, то натягиваемый стержень надо в этом сечении снова расположить в крайней точке ядра сечения, чтобы избежать возникновения вверху растягивающих напряжений. Следовательно, натягиваемый стержень должен быть искривлен. Таковы простые основные идеи применения предварительно напряженного железобетона, вытекающие из рассмотрения условий работы при изгибе. Если искусственно созданные сжимающие напряжения достаточны по величине и действуют именно в тех сечениях, где впоследствии возникнет растяжение, то, действительно, возможно избежать образования трещин в бетоне и таким образом устранить причины более раннего разрушения, вызываемого их появлением.
№30 1) 2) Определим требуемое количество канатов К-7, исходя из того что площадь одного каната 3) Определение необходимого усилия предварительного натяжения арматуры, проверка прочности сечения на разных стадиях работы 4) Приведенная площадь 5) Статический момент приведенной площади относительно нижней кромки сечения 6) Удаление yн центра тяжести приведенного сечения от нижней кромки сечения 7) Удаление yв центра тяжести приведенного сечения от верхней кромки сечения Момент инерции приведенного к бетону поперечного сечения 8) 9) Определим необходимую величину усилия предварительного натяжения в арматуре по условию трещиностойкости верхней кромки сечения в стадии эксплуатации по формуле
10) Проверим теперь прочность арматуры в момент создания усилия предварительного напряженияпо нижеприведенной формуле с учетом нормативного сопротивления арматуры.
1) №31 2) Определим требуемое количество канатов К-7, исходя из того что площадь одного каната 3) Определение необходимого усилия предварительного натяжения арматуры, проверка прочности сечения на разных стадиях работы 4) Приведенная площадь 5) Статический момент приведенной площади относительно нижней кромки сечения 6) Удаление yн центра тяжести приведенного сечения от нижней кромки сечения 7) Удаление yв центра тяжести приведенного сечения от верхней кромки сечения Момент инерции приведенного к бетону поперечного сечения 8) 9) Определим необходимую величину усилия предварительного натяжения в арматуре по условию трещиностойкости верхней кромки сечения в стадии эксплуатации по формуле
10) Проверим теперь прочность арматуры в момент создания усилия предварительного напряженияпо нижеприведенной формуле с учетом нормативного сопротивления арматуры.
№33 Расположение напрягаемой арматуры в продольном направлении в Огибающая эпюра изгибающих моментов в разрезной балке близка к параболе. В связи с этим наиболее целесообразной траекторией пучков напрягаемой арматуры по длине разрезных балок, как это уже было рассмотрено на предыдущих лекциях, является парабола. Необходимое количество пучков в середине пролета следует определять по А формуле ns=^ Ар где Ар - необходимая площадь напрягаемой арматуры в середине пролета, А1р - принятая площадь сечения одного пучка напрягаемой арматуры , Пучки напрягаемой арматуры необходимо размещать симметрично относительно продольной оси. Помимо пучков напрягаемой арматуры балки пролетных строений армируются конструктивной ненапрягаемой арматурой в соответствии с конструктивными требованиями. Сильно обжатые нижние пояса следует армировать хомутами, охватывающими напрягаемую арматуру.(см.рис.13.1)
№34 Неразрезные монолитные пролетные строения, возводимые методом циклической продольной надвижки с конвеерно- тыловым бетонированием. При надвижке пролетного строения любое поперечное сечение пролетного строения оказывается на промежуточных опорах и в середине пролета(рис. 13.2).
Рис.13.2.Схема возведения пролетного строения циклической продольной надвижкой с конвеерно- тыловым бетонированием. В связи с этим в каждом сечении по длине может от собственного веса возникнуть как положительный, так и отрицательный изгибающий момент. Это требует напрягаемой арматуры по всей длине пролетного строения в его нижнем и верхнем поясах (рис..13.3)
Рис.13.3.Схема армирования пролетного строения, возводимого циклической продольной надвижкой. 1-глухой концевой анкер; 2- продольная напрягаемая арматура по верхнему поясу; 3-концевые анкера раздельных арматурных элементов; 4- продольная напрягаемая арматура по нижнему поясу; 5- участки арматуры, очерченные по параболе Кроме того, для восприятия объемлющей эпюры моментов в стадии эксплуатации требуется дополнительно напрягаемая арматура по всей длине пролета, которой следует давать параболическое очертание. Напрягаемая арматура размещается в закрытых каналах. Горизонтальная арматура 2 и 4 на каждом этапе подвергается предварительному натяжению в период, предшествующий очередному циклу надвижки. Непрерывная криволинейная арматура натягивается после установки надвинутого пролетного строения на постоянные опоры. При этом потери напряжения в криволинейной арматуре на большой длине весьма велики. В связи с этим криволинейную арматуру выполняют раздельными арматурными элементами 5 (см. рис. 13.3) Следует иметь в виду, что в шве бетонирования можно стыковать не более половины пучков напрягаемой арматуры. Стык горизонтальных пучков осуществляется с помощью специальных устройств, получивших название «куплер». Ниже на рис. 13.4.приведена конструкция отечественного «куплера» для стыкования 19 канатов. Она выполнена в виде круглой плиты, в средней части которой имеются
конусные отверстия под трехдольные клинья для закрепления пучков одного направления, а по внешнему контуру выточены продольные прорези, в которые, после натяжения пучков первого направления, устанавливаются пучки второго направления с обжимными анкерами на концах. При использовании отверстий только одного направления этот анкер может быть использован в качестве глухого концевого.
В качестве глухого анкера используется также конструкция типа «фонарик». Этот тип анкера(рис.13.5) изготавливают путем предварительного раскручивания и осаживания конца каната на длине около 200 мм. При осаживании проволоки в пластической стадии расходятся в поперечном направлении и образуют» фонарик» диаметром 100мм и длиной 150 мм. Зона передачи усилия на бетон при такой анкеровке составляет не менее 840мм.. Требуемая площадь верхней горизонтальной напрягаемой арматуры определяется расчетом из условия восприятия максимального отрицательного момента на опоре от собственного веса при надвижке с аванбеком. Требуемая площадь нижней горизонтальной напрягаемой арматуры определяется расчетом из условия восприятия максимального положительного момента в середине пролета от собственного веса при надвижке с аванбеком. Горизонтальные пучки арматуры используются в последующей работе пролетного строения в стадии эксплуатации.
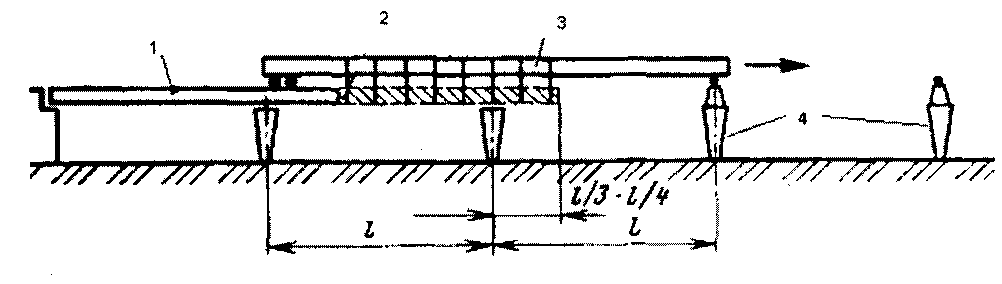
№35 . Неразрезные монолитные пролетные строения, возводимые на перемещаемых подмостях. На рис. 13.6 приведена схема возведения пролетного строения на перемещаемых подмостях Стык участков пролетного строения осуществляется в зоне минимальных моментов на удалении 1/3- 1/4 от промежуточной опоры.
Рис. 13.6. Схема возведения пролетного строения на перемещаемых ПОДМОСТЯХ: 1- готовая часть пролетного строения; 2- бетонируемая очередная часть пролетного строения; 3- перемещаемые подмости; 4- промежуточные опоры При таком возведении пролетного строения по его длине от собственного веса формируются расчетные силовые факторы как в неразрезной балке. Это позволяет использовать напрягаемую криволинейную арматуру, располагаемую в пределах пролета по параболе(рис.13.7).
Рис.13.7. Схема армирования продольной напрягаемой арматурой пролетных строений, ВОЗВОДИМЫХ на перемещаемых ПОДМОСТЯХ: 1-куплер; 2- разведенные по высоте пучки в стыке; 3-пучки напрягаемой арматуры, очерченные по параболе Арматуру при этом также располагают в закрытых каналах, но её анкеровку производят в швах бетонирования. Стык располагают чаще всего в четверти пролета. Такое расположение стыка позволяет развести соединение арматуры на некоторой высоте сечения с соблюдением условий обжатия, близкого к центральному. Все арматурные элементы над опорой необходимо поднимать как можно выше к верхней растянутой грани.
№36 . Неразрезные монолитные пролетные строения, возводимые методом навесного бетонирования. На рис. 13.8 приведена схема возведения пролетного строения навесным бетонированием. Этот метод используется при пролетах более 40 м. Бетонирование производится в подвесной опалубке уравновешенным способом от опор к середине пролета. При навесном бетонировании пролетные строения могут иметь переменную высоту ( обычно при пролетах более 84м).
Рис. 13.8 Схема возведения пролетного строения методом навесного бетонирования: 1- передвижные тележки для перемещения опалубки; 2- опалубка и подмости для навесного бетонирования..
Рис. 13.9. Армирование коробчатого пролетного строения при навесном бетонировании: №1-6 - номера арматурных элементов.; узел I: 1- анкер напрягаемой арматуры.:2- канал и пучок напрягаемой арматуры в нем;3- железобетонный прилив в нижней плите пролетного строения; 4- стенка коробки пролетного строения. При возведении пролетного строения этим способом от собственного веса по всей длине консоли формируется отрицательный момент. В середине пролета в момент замыкания от собственного веса изгибающий момент будет равен нулю. После замыкания пролетного строения от второй части собственного веса и временной нагрузке в нем формируются силовые факторы как в неразрезной балке. С учетом этого арматурные пучки располагают в верхней растянутой зоне консоли в пределах плиты проезжей части и стенок коробки(рис.13.9). Некоторую часть арматурных элементов верхней плиты заводят в стенки для анкерения. При замыкании пролетного строения в середине пролета в нижней плите устанавливается арматура для восприятия положительных изгибающих моментов. Анкеры этой арматуры устраивают в приливах нижней плиты(см.узел I на рис. 13.9). Напрягаемую арматуру рекомендуется размещать в закрытых каналах. По закрытым каналам представляется возможным переводить в верхней плите в плане и переводить затем в ребра для улучшения их работы на поперечные силы. На рис. 13.9 приведена схема армирования коробчатого пролетного строения в плане и профиле с демонстрацией перевода арматуры из плиты в ребра. Применение криволинейной в плане и профиле арматуры , размещенной в закрытых каналах, позволяет создать более надежную конструкцию. Каналы после натяжения пучков необходимо инъектировать цементным раствором. Кроме напрягаемой арматуры, неразрезные пролетные строения армируются и конструктивной арматурой. Ниже на рис. 13.10 приведена схема поперечного армирования ненапрягаемой арматурой коробчатого и плитно-ребристого сечений.
Рис. 13.10 Армирование коробчатого сечения ненапрягаемой арматурой. В верхней плите, в зоне действия отрицательных изгибающих моментов от местного действия временной нагрузки установлена верхняя сетка с рабочими поперечными стержнями, поставленными по расчету. В средней части верхней плиты верхняя сетка поставлена без расчета по конструктивным соображениям. Сетки соединены внахлестку. В средней части плиты нижняя сетка имеет поперечные стержни рабочей арматуры, рассчитанной на восприятие положительного момента. Стенки коробки армированы сетками с поперечными стержнями( хомутами), поставленными по расчету на прочность наклонных сечений при воздействии поперечной силы от изгиба всей балки. Остальные сетки поставлены без расчета по конструктивным соображениям (противоусадочная, распределительная и монтажная арматуры).
Рис.13.11. Армирование плитно-ребристого пролетного строения ненапрягаемой арматурой. Поперечное сечение плитно-ребристой конструкции, кроме пучков напрягаемой арматуры, имеет следующие элементы армирования ненапрягаемой арматурой: А-1-верхнюю сетку плиты проезжей части; А-П- арматурный каркас секции бетонирования, включающий арматурный каркас главных ребер, нижнюю сетку консолей и рабочую арматуру средней плиты.
№38 Определение усилий в опоре от постоянной и временной нагрузки Усилия в опорах мостов определяются при загружении линий влияния опорной реакции постоянными и временными нагрузками. Линия влияния опорной реакции строится в зависимости от вида опоры ( промежуточная или крайняя) и статической схемы пролетного строения (разрезное или неразрезное). Для неразрезных пролетных строений линии влияния опорных реакций имеют следующий вид: а)для крайней опоры
Линии влияния опорных реакций для опор неразрезных пролетных строений строятся с использованием таблиц, имеющихся в справочниках. При этом линия влияния опорной реакции на промежуточной опоре получается суммированием ординат линий влияния поперечных сил слева и справа от опорного сечения. Знаки линии влияния поперечной силы слева при этом следует поменять на обратные. Полученные линии влияния опорных реакций загружаются постоянной нагрузкой ( её первой и второй частью) по всей её длине, а также временными нагрузками. При загружении временной нагрузкой полосовая нагрузка от АК и тротуарная нагрузка размещаются в пределах однозначных участков линии влияния, а тележка от АК размещается над максимальными ординатами линии влияния. При загружении нагрузкой типа НК-80 одна из её осей размещается над максимальной ординатой линии влияния, а остальные размещаются рядом невыгодным образом в соответствии с расстояниями между осями нагрузки НК-80. Площади положительных ($ и отрицательных ф _ участков линии влияния вычисляются приближенно методом трапеций по известным их ординатам в определенных точках через 1/6 пролета. Полное вертикальное усилие на элемент промежуточной опоры от веса пролетного строения и временной нагрузки типа АК определяется на основе загружения линии влияния по формуле: Vq = ^nJfnK + ^euJfeus + ^rfq^+ + (0.) + qmrfm77m(Omax + + РтеЛГ1рГ/р(1+^(у1+у2)+УГ/у77г(1+^С(}тах Коэффициенты поперечной установки для элементов промежуточной опоры вычисляются с учетом конструктивного решения опоры.
№39 . Определение усилий в опоре от сил торможения. Исходя из условия создания наиболее невыгодной ситуации, обычно исходят из того, что тормозят транспортные средства, движущиеся только в одном направлении. Нормативную горизонтальную продольную нагрузку от торможения равномерно распределенной части нагрузки АК принимается равной 50 % веса этой нагрузки на загружаемой линии влияния, но не менее 7.8К кН (0,8К тс) и не более 24,5К кН (2,5К тс.). Продольную нагрузку принимают с учетом всех полос одного направления. При этом учитывается коэффициент S1. Расчетная формула для силы торможения имеет вид: 7.8 к <=т> = 0.5ут]Л<=24.5К Сила торможения прикладывается в уровне проезжей части при расчете устоев и на уровне центров опорных частей при расчете промежуточных опор. Сила торможения полностью передается через неподвижные опорные части. Подвижные опорные части могут воспринимать часть силы торможения силами трения, возникающими в них при минимальных значениях коэффициентов трения или качения. Силы торможения в промежуточной опоре вызывают изгибающий момент на плече от центра опорных частей до рассматриваемого сечения ( например низа опоры).
№40 Определение усилий в опоре от боковых ударов нагрузки АК. Известно, что боковые удары от нагрузки типа АК возникают при переходе нагрузки из одной полосы движения в другую. Нормативная горизонтальная поперечная нагрузка от ударов нагрузки АК принимается в виде равномерно распределенной нагрузки, равной 0.39 К в кН/м (0.4 К в тс/м) или сосредоточенной силы, равной 5.9 К в кН (0,6 К в тс), приложенных в уровне верха покрытия проезжей части. При действии горизонтальной поперечной нагрузки статическая схема пролетного строения такая же, как и при действии вертикальной нагрузки. В связи с этим горизонтальная поперечная нагрузка на опору может быть определена по линии влияния, построенной для опорной реакции. Горизонтальная сила от бокового удара нагрузки АК определится по формуле: Н=0-4^ол^+втс. Сила Н создает в опоре изгибающий момент на плече, равном расстоянию от уровня проезжей части до рассматриваемого сечения( низа опоры).
№41 от ледохода и навала судов Определение усилий на опору от ледохода. Производится в Определение усилий на опору от навала судов. Производится в соответствии с п. 2.26 СНиП 2.05.003-84*.
№42 Расчет на прочность сжатых железобетонных элементов мостов с расчетным эксцентриситетом e0 <r ( п. 3.69).
Предварительно заметим, что распложенную в сжатом элементе напрягаемую арматуру, имеющую сцепление с бетоном , прочность которого используется полностью, в расчет следует вводить с напряжением σpc=-(Rpc- σpc1) (A) которое является разностью (взятой с противоположным знаком) ,расчетного напряжения σpc1 в напрягаемой арматуре с учетом всех потерь и наибольшего напряжения Rpc=500МПа в напрягаемой арматуре в сжатой зоне. При σPC1<RPC σpc =0
С учетом этого формула для расчета прочности сжатых железобетонных элементов при наличии сцепления всей арматуры с бетоном .будет иметь вид (17.1). N+ σpcAp≤ (Rb Ab+RscAs'+RPcAp) (17.1) В правой части соотношения (17.1) несущая способность сечения сжатого железобетонного элемента с ненапрягаемой .и напряженной арматурой. При этом: RbAb- вклад бетона в несущую способность сечения при полном использовании его прочности; RscAs' - ненапрягаемой арматуры в несущую способность сечения при полном использовании прочности бетона, которому соответствует полное использование прочности ненапрягаемой арматуры Rsc = Rs ; RPcAp - вклад напрягаемой арматуры в несущую способность сечения при реализуемом при этом в ней уровне напряжений R = 500МПа.
В левой части соотношения (17.1) - внешняя сжимающая сила. Она состоит из двух слагаемых : внешней силы N, создаваемой постоянной и временной нагрузками, и внешней силы σpcAp создаваемой частью непогашенного сжатием усилия предварительного натяжения арматуры. Из (17.1) с учетом (А) получаем расчетную формулу для определения внешней силы N, N≤ (Rb Ab+RscAs'+RPcAp) -σpcAp = Rb Ab+RscAs' -σpc1Ap (17.1) Формула для расчета устойчивости сжатых железобетонных элементов при наличии сцепления всей арматуры с бетоном будет иметь вид (17.2) N+σpcAp ≤ φ(Rb Ab+RscAs'+RPcAp) Откуда N≤ φ(Rb Ab+RscAs'+RPcAp) -σpcAp
При отсутствии сцепления напрягаемой арматуры с бетоном все сжимающие усилия в элементе воспринимаются приведенным сечением
После приложения усилия N к элементу, ранее приложенное усилие σpc1Ap от напрягаемой арматуры уменьшится на величину
В левой части формулы для расчета прочности и устойчивости сжатых элементов с напрягаемой арматурой, не имеющих сцепления с бетоном, внешние силы будут иметь следующий вид
Её физический смысл сводится к следующему: усилие N вызовет в приведенном к бетону сечении относительную деформацию сжатия
, что уменьшит величину предварительного натяжения в напрягаемой арматуре на
Простое преобразование (А) приводит к следующим формулам
где n1 =Es/Eb отношение модулей упругости, μ=As/Ab -коэффициент армирования
В связи с отмеченной особенностью при отсутствии сцепления напрягаемой арматуры с бетоном расчет устойчивости сжатых элементов следует проверять по формуле (17.3)
а прочности по формуле (17.4)
№43 Расчет на прочность внецентренно -сжатых железобетонных элементов мостов таврового, двутаврового и коробчатого сечений с плитой в сжатой зоне с расчетным эксцентриситетом e0 > г и при х >hf производится по п. 3.70 с использованием условия
при этом величина e()=e +ес(η-1). Формула для эксцентриситета учитывает деформированное состояние стержня. Ниже дается её обоснование.
e()- эксцентриситет в наиболее напряженном сечении с учетом деформирования оси сжатого элемента; Заметим, что е = а + ес- расстояние от точки приложения силы до равнодействующей усилий в растянутой арматуре в верхнем сечении элемента(см. рис); ес- начальный эксцентриситет продольной силы относительно центра тяжести всего сечения( с учетом случайного эксцентриситета) Учтем, что а = е - ес (см.рис) Тогда в деформированном состоянии максимальный эксцентриситет равен e0= а +есη = е - ес+ есη = е +ес(η-1) Остальные обозначения в формуле (I) понятны из приведенных рисунков. Для прямоугольного сечения в формуле (I) принимается bf =b
№44 Расчет внецентренно - сжатых железобетонных элементов мостов кольцевого сечения.
Для расчета на прочность элементов кольцевого сечения используются формулы, обеспечивающие достаточную для практических расчетов точность при соотношении внутреннего и наружного диаметров r2>0.5r1 и ненапрягаемой арматуре, состоящей не менее чем из шести стержней, равномерно распределенных по окружности. Они приведены в СНиП 2.05.03-84 . Ниже дается вывод этих формул и принятые при этом допущения
Схема для расчета внецентренно сжатого кольцевого сечения При выводе формул считается, что: 1. Арматура равномерно распределена по окружности радиуса га равного расстоянию от центра сечения до арматурных стержней. 2. Напряжения в бетоне и арматуре сжатой зоны равны их расчетным сопротивлениям Rь и Rs 3. Напряжения в арматуре растянутой зоны зависят от положения стержней, средние напряжения в ней равны σsRs. 4. Равнодействующая усилий в растянутой арматуре проходит на расстоянии Zs от оси сечения.
Представим относительную площадь сжатой зоны бетона как
где rm = (r1 - r2) / 2 Из (1) получаем значение угла, ограничивающего сжатую зону,
α=ξcirπ (2)
Учтем далее, что расстояние от центра тяжести площади сжатого бетона до центра всего сечения определяется формулой
а расстояние от равнодействующей усилий в сжатой арматуре до центра сечения
Принимая затем площадь арматуры равномерно распределенной по окружности радиуса rs, условие прочности с учетом прогиба элемента можно записать в таком виде:
Подставляя в (5) значения α, уs , уb получим
После сокращения на ξcir получаем
Значения zs и φs определяются по эмпирическим формулам: zs=(0.2+1.3 ξcir)rs φs=1-1.7 ξcir
Относительную площадь сжатой зоны бетона находят из условия равенства нулю суммы проекций всех сил на горизонтальную ось: N+RsAsφs=RbAb ξcir +RsAs ξcir
После-замены φs=1-1.7 ξcir и приведения подобных членов получаем
Если при этом будет получено ξcir ≤0.15, т.е. при относительно малой площади сжатого бетона, то прочность сечения проверяют по условию
где ( при ξcir >6 ) влиянием растянутой арматуры пренебрегают( φs = 0) и прочность сечения проверяют по условию:
При малых эксцентриситетах ( с учетом случайного) продольной силы, когда она не выходит за пределы ядра сечения, то сечение следует проверять на устойчивость по формуле
№45 Теоретические основы расчета деформаций пролетных строений железобетонных мостов. Определение деформаций пролетных строений железобетонных мостов: прогибов и углов поворота.
В качестве теоретической основы расчета деформаций пролетных строений железобетонных и других мостов используется интеграл Мора.
где Δmn- перемещение по направлению фиктивной единичной силы Р=1, вызванное действием реальной произвольной группы сил n. - Мm(Х) - изгибающий момент от фиктивной единичной нагрузки в функции координаты X произвольного сечения, - Мn(Х) - изгибающий момент от заданной нагрузки в функции координаты X произвольного сечения
При решении задачи рассматривается два состояния пролетного строения:
а. В первом его (действительном) состоянии на него действует реальная система сил.
б.Во втором (единичном или фиктивном) состоянии к пролетному строению приложена лишь одна сосредоточенная фиктивная сила.
При вычислении прогиба в какой- то точке по длине пролета, в качестве единичной силы служит безразмерная фиктивная сосредоточенная сила, приложенная в этой точке. При вычислении угла поворота в какой то точке пролетного строения в качестве единичной силы выступает сосредоточенный безразмерный фиктивный момент, приложенный в той же точке.
в.Находятся выражения Мn (X) и Mm (X), подставляются в правую часть формулы (1) и при интегрировании по участкам в пределах всего пролетного строения определяется искомое перемещение Δmn. Если Δmn положительно, то перемещение совпадает с направлением единичной силы, а если отрицательно, то противоположно этому направлению.
Поиск по сайту: |
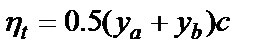

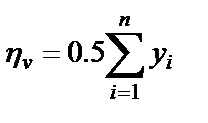




 и обжатия бетона
и обжатия бетона 

 - требуемая площадь напрягаемой арматуры
- требуемая площадь напрягаемой арматуры сечения определим по формуле
сечения определим по формуле 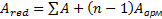



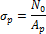














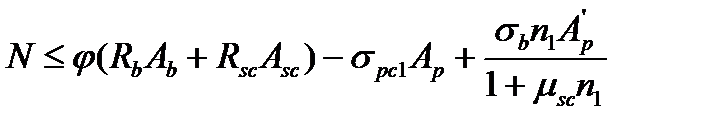 (17-3)
(17-3) (17-4)
(17-4) (I)
(I)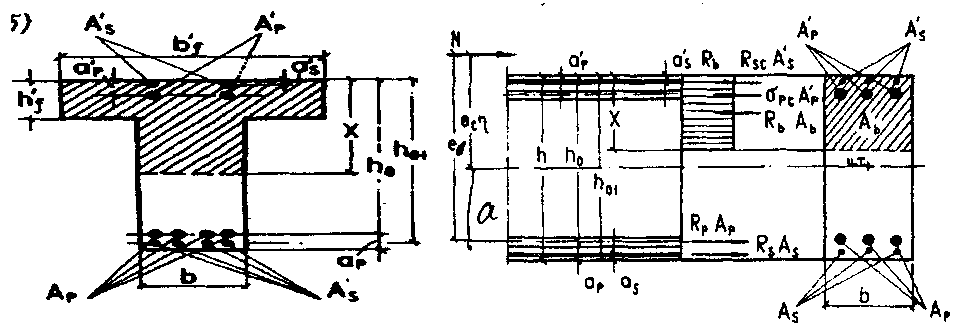

 (1)
(1)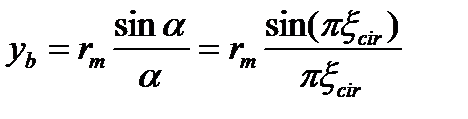 (3)
(3)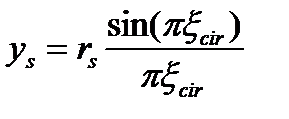 (4)
(4) (5)
(5)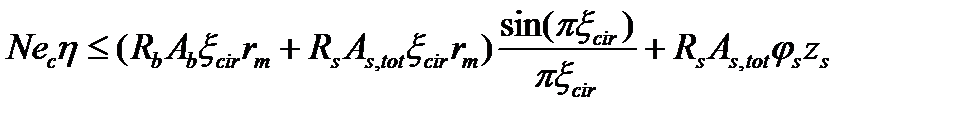 (5)
(5) (5)
(5)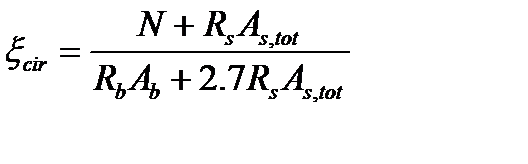
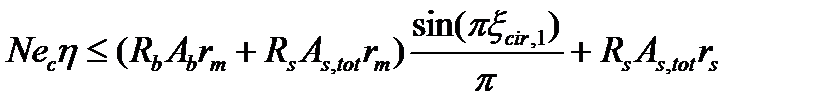 (5)
(5) , а при значительной площади сжатого бетона
, а при значительной площади сжатого бетона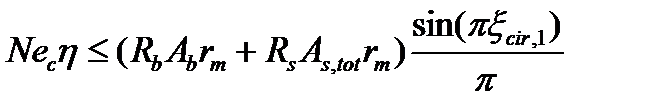 , в котором
, в котором
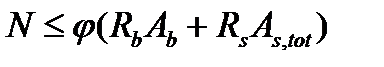
 (1)
(1)