 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгебраическая форма комплексного числаСтр 1 из 4Следующая ⇒
Комплексные числа и элементарные функции комплексного переменного Учебно- методическое пособие для студентов технических специальностей Ижевск Издательство ИжГТУ УДК
Рецензент Селетков С.Г., д.т.н., проф., зав. кафедрой
Составители: Гусельникова Г.В. ,канд. физ.-мат. наук, проф., Ракита Н.В., доц. Рекомендовано к изданию на заседании кафедры «Высшая математика» ИжГТУ (протокол № от декабря 2011 г.) Комплексные числа и элементарные функции комнлексного переменного :учеб.- метод. пособие / составители: Г.В. Гусельникова, Н.В. Ракита. УДК Учебно- методическое пособие предназначено для самостоятельной работы студентов , изучающих данный раздел математики как вспомогательный материал для основной программы. Может быть использовано как дополнительный ресурс студентами, изучающими функции комплексного переменного по программе. Г.В. Гусельникова, Н.В. Ракита, составление, 2011 Ижевский государственный технический университет, 2011 КОМПЛЕКСНЫЕ ЧИСЛА Понятие комплексного числа. Алгебраическая форма комплексного числа.
Рис. 1 Каждому комплексному числу Вектору Определение. Комплексное число Определение. Два комплексных числа
Определение. Суммой двух комплексных чисел Очевидно, Определение. Произведением двух комплексных чисел Очевидно, Из предыдущих определений следуют равенства:
Комплексное число ►Действительно, Определение.
алгебраическая форма комплексного числа Покажем, что вычисление суммы и произведения двух комплексных чисел в алгебраической форме можно производить по правилам сложения и умножения алгебраических многочленов, т.е. ►Пусть
Учитывая, что Произведение действительного числа ►Действительно, Сумма двух комплексных чисел обладает следующими очевидными свойствами:
Геометрически сумму двух комплексных чисел Непосредственной проверкой Рис. 2 можно установить, что произведение двух комплексных чисел обладает следующими свойствами:
Пример 1. Составить квадратное уравнение, корни которого равны Решение. Пусть Тогда
Число, сопряженное числу Рис. 3 Пример 2. Вычислить Решение. Пример 3. Решить уравнение Решение. Преобразуем уравнение Решая полученную систему, имеем Определение. Число
Очевидно, модуль комплексного числа Разность Частное Пример 4. При каких действительных значениях Решение.
Пример 5. Решить уравнение Решение.
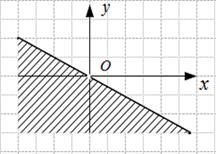
Пример 6. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству Решение.
удовлетворяют все точки заштрихованной полуплоскости, исключая начало координат(рис. 4). ● Пример 7. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству
Пример 8. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству
Рис. 6
Пример 9. Изобразить на комплексной плоскости множество точек, удовлетворяющих системе неравенств
Решение.
Указанной системе неравенств удовлетворяют точки заштрихованной области (рис. 7).● Рис. 7 Модуль разности чисел Пусть Множество точек Неравенству Например, уравнение Пример 10. Найти множество точек, удовлетворяющих неравенствам Решение. Искомое множество должно одновременно удовлетворять неравенствам Пример 11 Определить тип линии, заданной уравнением Решение. Так как (Эллипс есть геометрическое место точек, для каждой из которых сумма расстояний от двух фиксированных точек есть величина постоянная). ● Пример 12. Найти множество точек плоскости, Решение. Так как расстояние точки Если уравнение линии в декартовой системе координат задано в параметрической форме Например, уравнение Пример 13. Определить линии, заданные уравнениями: 1) 3) Решение. 1) Уравнение 2) 3)
Рис. 9 Рис. 10 Рис. 11 4)
Поиск по сайту: |
 Определение. Комплексным числом
Определение. Комплексным числом 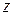 называется упорядоченная пара действительных чисел
называется упорядоченная пара действительных чисел  При этом действительное число
При этом действительное число 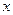 называется действительной частью комплексного числа
называется действительной частью комплексного числа 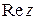 , а действительное число
, а действительное число 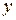 называется мнимой частью числа
называется мнимой частью числа  .
.
 и вектор
и вектор  плоскости
плоскости  (рис. 1), при этом плоскость
(рис. 1), при этом плоскость  .
. ставится в соответствие действительное число
ставится в соответствие действительное число  , т. е.
, т. е. 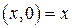 , а вектору
, а вектору  ставится в соответствие число 1, т. е.
ставится в соответствие число 1, т. е. 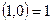 . Началу координат, т. е. вектору
. Началу координат, т. е. вектору  ставится в соответствие число 0.
ставится в соответствие число 0. называют мнимой единицей и обозначают
называют мнимой единицей и обозначают  .
. и
и  называются равными в том и только в том случае, если равны их действительные и равны их мнимые части, т.е.
называются равными в том и только в том случае, если равны их действительные и равны их мнимые части, т.е. или
или  .
. .
.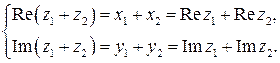
 .
.
 ,
, ,
, ,
, ,
, .
. может быть представлено в форме
может быть представлено в форме  или
или  .
. .◄
.◄ - (1)
- (1) и
и  .
. и
и 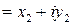 . Тогда
. Тогда 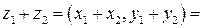
 .
. , имеем
, имеем 
 ◄
◄ на комплексное число
на комплексное число  .
. ,
,  , т.е.
, т.е.  .◄
.◄ (коммутативность сложения);
(коммутативность сложения);
 (ассоциативность сложения).
(ассоциативность сложения). и
и 
 (коммутативность произведения);
(коммутативность произведения);
 (дистрибутивность).
(дистрибутивность).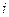 может быть определено как
может быть определено как  .
. и
и  .
. искомое квадратное уравнение. По теореме Виета
искомое квадратное уравнение. По теореме Виета  и
и  .
.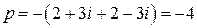 ,
,  и искомое уравнение имеет вид
и искомое уравнение имеет вид  .
.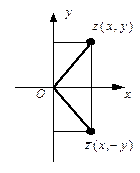 Определение. Два комплексных числа, действительные части которых равны, а мнимые части равны по модулю, но противоположны по знаку, называются сопряжёнными.
Определение. Два комплексных числа, действительные части которых равны, а мнимые части равны по модулю, но противоположны по знаку, называются сопряжёнными. и
и  (рис. 3).
(рис. 3).  и
и ..
.. и
и  .
.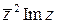 , если
, если 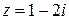 .
.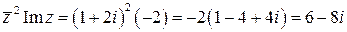 .●
.● .
.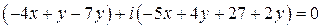 , откуда следует
, откуда следует  .
. .
.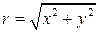 называют модулем комплексного числа
называют модулем комплексного числа 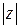 .
. . (2)
. (2) .
.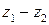 двух комплексных чисел
двух комплексных чисел 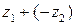 . Тогда
. Тогда  .
.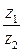 двух комплексных чисел
двух комплексных чисел 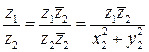 .
.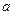 и
и 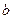 выполняется условие
выполняется условие  , если
, если  и
и  ?
? .
. и
и  , откуда
, откуда  и
и  ,
,  ●
● .
. ,
,  ,
,  и
и  ,
,  . Все точки параболы
. Все точки параболы  являются решениями данного уравнения. Уравнение имеет бесконечное множество решений. ●
являются решениями данного уравнения. Уравнение имеет бесконечное множество решений. ● .
.



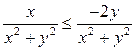

 .
. Решение.
Решение. 



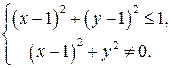
 , исключая точку
, исключая точку  .
. Решение.
Решение. 




 с центром в точке
с центром в точке  , исключая точку
, исключая точку 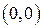




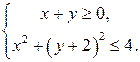
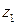 и
и  равен
равен 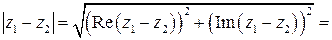 ,
,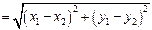 , откуда следует, что
, откуда следует, что  есть расстояние между точками с координатами
есть расстояние между точками с координатами 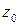 - данное комплексное число (данная точка),
- данное комплексное число (данная точка),  - данное действительное число.
- данное действительное число. , есть множество точек плоскости, отстоящих от точки
, есть множество точек плоскости, отстоящих от точки  , в частности,
, в частности, 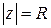 - окружность радиуса
- окружность радиуса 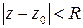 , удовлетворяют очки, отстоящие от точки
, удовлетворяют очки, отстоящие от точки  определяет окружность радиуса
определяет окружность радиуса  с центром в точке
с центром в точке 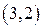 , а неравенство
, а неравенство  определяет внутренность и границу круга радиуса
определяет внутренность и границу круга радиуса  , Изобразить найденное множество на плоскости.
, Изобразить найденное множество на плоскости.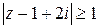 и
и 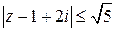 . Первое неравенство определяет внешность единичного круга с центром в точке
. Первое неравенство определяет внешность единичного круга с центром в точке 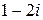 , а второе – внутренность круга радиуса
, а второе – внутренность круга радиуса  с центром в точке
с центром в точке 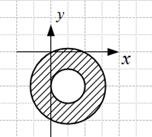 ограниченное концентрическими окружностями радиусов
ограниченное концентрическими окружностями радиусов  и
и 
 есть сумма расстояний точки
есть сумма расстояний точки 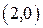 и
и  , то
, то  определяет эллипс с фокусами в точках
определяет эллипс с фокусами в точках  .
. в два раза больше, чем от точки
в два раза больше, чем от точки  .
. равно
равно 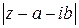 , то из условия задачи имеем
, то из условия задачи имеем  , откуда
, откуда 



 - множество точек окружности радиуса
- множество точек окружности радиуса  с центром в точке
с центром в точке 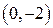 .●
.● то уравнение этой же линии в плоскости
то уравнение этой же линии в плоскости 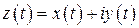 .
.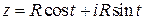 является уравнением окружности радиуса
является уравнением окружности радиуса 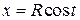 ,
,  и
и  .
.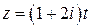 ; 2)
; 2)  ;
; ; 4)
; 4)  .
. ,
,  и
и  .
. ,
,  и
и  - гипербола (рис. 9);
- гипербола (рис. 9); ,
,  и
и  , т.е.
, т.е. 
 ,
,  и
и 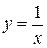 , причём,
, причём,  Следовательно,
Следовательно, 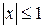 (рис. 11).
(рис. 11).