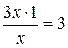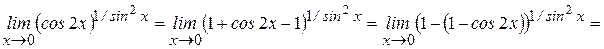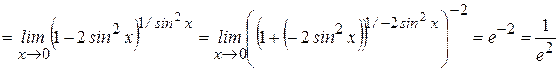|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЙ ⇐ ПредыдущаяСтр 3 из 3
Для успешного вычисления пределов функций необходимо знать следующие теоремы: 1) 2) 3) если
4) 5) 6) I и II замечательные пределы:
Рассмотрим сначала непосредственное нахождение предела функции: Пример 1: Найти Проверим, не обращается ли значение знаменателя в нуль при
Подставим предельное значение функции и получим:
Пример 2: Если предел делителя равен 0, а предел делимого есть число, отличное от нуля, то предел дроби не существует или дробь имеет бесконечный предел:
Пример 3:
Так как
Пример 4:
Пример 5:
Иногда при подстановке в функцию предельного значения аргумента получаются выражения вида:
Их называют «неопределенностями». В этих случаях для нахождения предела необходимо предварительно выполнить некоторые преобразования данного выражения. Рассмотрим некоторые приемы. Пример 1: Вычислить
Пример 2: Вычислить
Пример 3: Вычислить
Итак, чтобы найти предел частного двух функций, где пределы числителя и знаменателя равны 0, нужно преобразовать функцию таким образом, чтобы выделить в делимом и делителе сомножитель, предел которого равен и сократить дробь на этот сомножитель, найти предел частного. Нужно знать формулы:
Пример 4:
Пример 5:
Пример 6:
Пример 7:
Рассмотрим примеры отыскания предела функции при Пример 8:
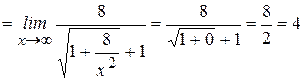
Знаменатель – бесконечно большая величина, а обратная ей – бесконечно малая величина, следовательно, Пример 9: Найти Преобразуем данное выражение, разделив числитель и знаменатель на
Пример 10:
Пример 11:
Пример 12:
Пример 13:
Пример 14:
Рассмотрим примеры, в которых используются I и II замечательные пределы.
Пример 15: Найти Пример 16:
При решении более сложных примеров нередко используют эквивалентность бесконечно малых величин. Две бесконечно малые величины при
то есть одну бесконечно малую величину можно заменить ей эквивалентной. Пример 17:
Пример 18:
Рассмотрим вычисление пределов с использованием II замечательного предела. Пример 19:
Пример 20:
а показатель степени Пример 21:
так как Пример 22:
так как
Пример 23:
План 2005/2006, поз.
Гресюк Татьяна Казимировна
КУРС ЛЕКЦИЙ
по дисциплине «ВЫСШАЯ МАТЕМАТИКА»
Теория пределов
для студентов заочной формы обучения
Редактор Н.В. Вердыш
Подписано к печати _______________ Формат 60х84/16 Усл. печ. л. _______уч.-изд. л. ______ Тираж __________ экз. Заказ _______
Учреждение образования «ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ» 220114, г. Минск, ул. Ф.Скорины 8, к. 2
ПОРЯДОК
Поиск по сайту: |
 , где
, где 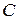 - постоянная;
- постоянная; , где
, где  и
и  существуют, то
существуют, то ,
,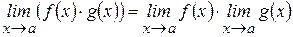 ;
; , если
, если  ;
; ;
; ,
,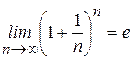 ,
,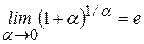 .
. .
. :
: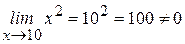 .
. .
. .
. .
.

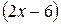 - бесконечно малая величина, а обратная ей
- бесконечно малая величина, а обратная ей  - бесконечно большая величина.
- бесконечно большая величина. ;
; .
.
 .
. .
. ;
;  ;
;  ;
; 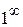 ;
;  .
.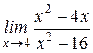
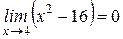


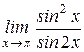



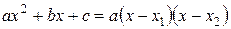
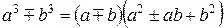



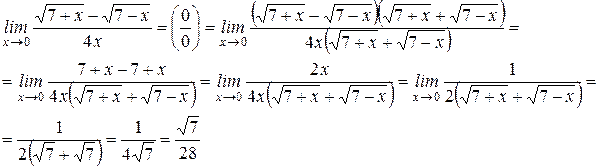
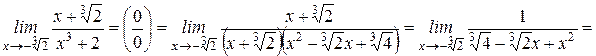
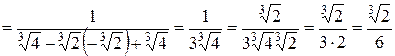


 .
.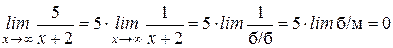
 .
. - числитель и знаменатель бесконечно большие величины, то есть неопределенность вида
- числитель и знаменатель бесконечно большие величины, то есть неопределенность вида  , получим:
, получим: , так как
, так как 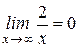 ;
;  .
.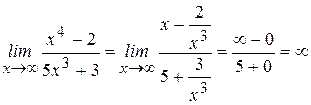 .
.









 ,
, 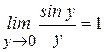
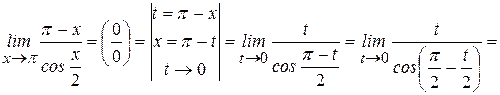

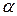 и
и 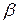 называются эквивалентными, если
называются эквивалентными, если  .
. ,
,  ;
; ,
,

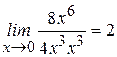
 , при
, при 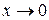
 , при
, при 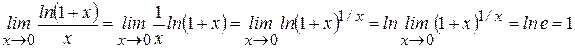
 , так как
, так как 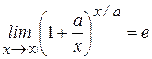 ,
,
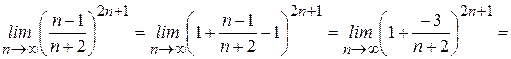
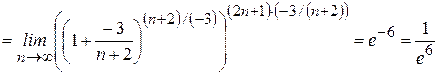 ,
, , а
, а 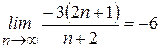 (смотрите свойство 5)
(смотрите свойство 5) ,
, , где
, где 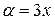 , а показатель степени
, а показатель степени