 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Примеры эквивалентных б.м ⇐ ПредыдущаяСтр 2 из 2
sin x ~ x; tg x ~ x; ℮x – 1 ~ x; ln(1 + x) ~ x; arcsin x ~ x; arctg x ~ x; (1 + x)m ~ 1 + mx; 1 – cos x ~ x2/2.
Замечательные пределы. I. II.
Определение. Функция f(x) называется непрерывной в точке х0, если она удовлетворяет следующим условиям: 1) определена в точке х0 (т. е. существует f(х0)); 2) имеет конечный предел функции при х → х0; 3) этот предел равен значению функции в точке х0 , т. е.
Задачи.
На основании непрерывности функции в точке х = 7 искомый предел равен значению функции в этой точке, т. е.
В рассматриваемых примерах предел находится сразу в виде числа или символа ∞. Чаще приходится сталкиваться с неопределенностями, когда результат нахождения предела неясен, например, когда рассматривается предел отношения двух б.м. величин (условное обозначение
Разложим числитель на множители и сократим на (х - 1). Сокращение возможно, т. к. при х → 1 выражение (х - 1) стремится к нулю, но не равно нулю.
Домножим числитель и знаменатель на выражение, сопряженное числителю:
=
=
=
Делаем замену
Замена
Замена
Это неопределенность вида
■ Для решения задач, где ищется предел дробно-рациональной функции (отношения двух многочленов), можно пользоваться следующим правилом: Пусть Рn = a0 + a1x + a2x2 + … + anxn и Qm = b0 + b1x + b2x2 + … + bmxm. Тогда
an /bm, если n = m. ■
16.
17.
18.
■ Это задача с использованием первого замечательного предела Обратим внимание на то, что при использовании первого замечательного предела нужно следить за аргументами частного под знаком предела. Они должны быть идентичны, т. е.
=
=
= =
25 ■ Это задача с использованием второго замечательного предела в первой форме
■ Это задача с использованием второго замечательного предела во второй форме
27 =
31 32
=
Поиск по сайту: |

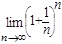 =
= 


 1.
1.  =
= =
=  = 13. ►
= 13. ►
 2.
2.  =
= При х → 8 числитель (2х — 7) стремится к 2∙8 — 7 = 9, т. е. является ограниченной функцией, а знаменатель (х — 8) стремится к нулю, т. е. является б.м. величиной. Отсюда по свойствам б.м. величин искомый предел = ∞. ►
При х → 8 числитель (2х — 7) стремится к 2∙8 — 7 = 9, т. е. является ограниченной функцией, а знаменатель (х — 8) стремится к нулю, т. е. является б.м. величиной. Отсюда по свойствам б.м. величин искомый предел = ∞. ►
 3.
3.  =
= Функция sin x есть функция ограниченная (|sin x| ≤ 1), а х - б.б. величина. Следовательно, искомый предел = 0.
Функция sin x есть функция ограниченная (|sin x| ≤ 1), а х - б.б. величина. Следовательно, искомый предел = 0. ), или двух б.б. величин (условное обозначение
), или двух б.б. величин (условное обозначение  ). В математическом анализе также рассматриваются неопределенности вида [∞ - ∞], [0 ∙ ∞], [1∞].
). В математическом анализе также рассматриваются неопределенности вида [∞ - ∞], [0 ∙ ∞], [1∞].
 4.
4.  =
=  =
=  =
=  = ∞. ►
= ∞. ► 5.
5.  =
=  =
=  =
=  .►
.► 6.
6.  =
=  =
=  .►
.► 7 .
7 .  =
= =
=  =
=  =
= =
=  . ►
. ► 8.
8.  =
=  =
= =
=  =
=  =4.►
=4.► 9.
9.  =
=  =
=  =
= ►
► 10.
10.  =
= (степень числителя 1/2, степень знаменателя 1/3, для замены берем степень с общим знаменателем для этих дробей), тогда
(степень числителя 1/2, степень знаменателя 1/3, для замены берем степень с общим знаменателем для этих дробей), тогда  При х → 1 имеем t → 1, отсюда
При х → 1 имеем t → 1, отсюда =
=  =
=  =
=  . ►
. ► 11.
11.  =
= , тогда
, тогда  При х → 1 имеем t → 1, отсюда
При х → 1 имеем t → 1, отсюда =
=  =
=  =
=  . ►
. ►
 =
=  =
= , тогда x = t3. При х → 1 t → 1, отсюда
, тогда x = t3. При х → 1 t → 1, отсюда =
=  =
=  =
=  . ►
. ►
 13.
13.  =
= =
=  =
=  = 0.►
= 0.► =
=  =
=  = ∞. ►
= ∞. ► =
=  =
=  =
=  . ►
. ► 0, если n < m,
0, если n < m, = ∞, если n > m,
= ∞, если n > m, = [старшая степень числителя n =
= [старшая степень числителя n =  , старшая степень знаменателя m = 2. Имеем n > m] = ∞. ►
, старшая степень знаменателя m = 2. Имеем n > m] = ∞. ► = [старшая степень числителя n =
= [старшая степень числителя n =  = 1, старшая степень знаменателя m =
= 1, старшая степень знаменателя m =  = 1. Имеем n= m] =
= 1. Имеем n= m] =  =
=  . ►
. ► = [старшая степень числителя n = 2, старшая степень знаменателя m = 3. Имеем n < m] = 0. ►
= [старшая степень числителя n = 2, старшая степень знаменателя m = 3. Имеем n < m] = 0. ►
 =
= .
.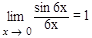 , т. к. аргумент и в числителе и в знаменателе 6х и при х → 0 6х также → 0, а вот
, т. к. аргумент и в числителе и в знаменателе 6х и при х → 0 6х также → 0, а вот  не является первым замечательным пределом, т. к. аргументы числителя и знаменателя не совпадают. ■
не является первым замечательным пределом, т. к. аргументы числителя и знаменателя не совпадают. ■ =
=  =
=  =
=  =
= 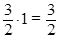 .►
.► =
=  =
=  =
=  =
=  = [замена у =
= [замена у =  , тогда если х → ∞, то у → 0] =
, тогда если х → ∞, то у → 0] = . ►
. ► 22.
22.  =
=  =
=  =
= =
=  =
=  =
=  = 1 ∙ 0 ∙ 1 = 0.►
= 1 ∙ 0 ∙ 1 = 0.► = [замена у = 1 — х, тогда если х → 1, то у → 0] =
= [замена у = 1 — х, тогда если х → 1, то у → 0] = =
=  =
=  =
= =1 :(
=1 :(  ∙ 1) =
∙ 1) =  .►
.►
 . Обратим внимание на то, что, как и при использовании первого замечательного предела, нужно следить за аргументами выражения в скобках и степени — они должны быть идентичны. Также заметим, что в обеих формах второго замечательного предела в скобках стоит сумма. ■
. Обратим внимание на то, что, как и при использовании первого замечательного предела, нужно следить за аргументами выражения в скобках и степени — они должны быть идентичны. Также заметим, что в обеих формах второго замечательного предела в скобках стоит сумма. ■ =
=  =
=  = ℮15. ►
= ℮15. ►
 26.
26.  =
= ■
■ =
=  =
= 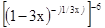 = ℮ -6. ►
= ℮ -6. ► =
=  =
=  =
= =
=  = ℮ -14. ►
= ℮ -14. ► = [это неопределенность вида
= [это неопределенность вида  . Заменяя sin 4x эквивалентной бесконечно малой 4х, получим ] =
. Заменяя sin 4x эквивалентной бесконечно малой 4х, получим ] =  = 2. ►
= 2. ► = [Заменяя
= [Заменяя  эквивалентной б.м. 5х2, а (1 - cos 2x) эквивалентной б.м.
эквивалентной б.м. 5х2, а (1 - cos 2x) эквивалентной б.м.  = 2x2, получим ] =
= 2x2, получим ] =  =
=  . ►
. ► = [Заменяя (1 + 3x)10 эквивалентной б.м. (1 + 30x), получим] =
= [Заменяя (1 + 3x)10 эквивалентной б.м. (1 + 30x), получим] =  = 5. ►
= 5. ► 34.
34.  =
=  =
=  =
= =
=  5 ∙ ln ℮6 = 5 ∙ 6 ∙ln ℮ = 30.►
5 ∙ ln ℮6 = 5 ∙ 6 ∙ln ℮ = 30.►