 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства б.м. и б.м. величинСтр 1 из 2Следующая ⇒
Пределы. Определение. Число А называется пределом функции y = f(x) при х, стремящемся к бесконечности, если для любого сколь угодно малого положительного числа ε > 0 найдется такое положительное число S > 0 (зависящее от ε : S = S(ε)), что для всех х таких, что |x| > S, верно неравенство |f(x) – A| < ε. (1) Этот предел функции обозначается
или f(x) → А при х → ∞. С помощью логических символов определение можно записать в виде
Смысл определения: при достаточно больших по модулю значениях х значения функции f(x) как угодно мало отличаются от числа А(по абсолютной величине).
Итак, число А есть предел функции y = f(x) при х → ∞, если для любого числа ε > 0 найдется такое число S > 0, что для всех х таких, что |x| > S, соответствующие ординаты графика функции f(x) будут заключены в полосе A- ε < у < A+ ε, какой бы узкой эта полоса не была. Замечание. Приведенное определение предела при х → ∞ предполагает неограниченное возрастание переменной х по абсолютной величине. Можно сформулировать понятие предела при стремлении х к бесконечности определенного знака, т. е. при х → +∞ и х → -∞. В первом случае основное неравенство (1) должно выполняться для всех х таких, что x > S, а во втором - для всех х таких, что x < -S. Предел функции в точке. Пусть функция y = f(x) задана в некоторой окрестности точки х0, кроме, может быть, самой точки х0. Определение. Число А называется пределом функции y = f(x) при х, стремящемся к х0,если для любого сколь угодно малого положительного числа ε > 0 найдется такое положительное число δ > 0 (зависящее от ε : δ = δ(ε)), что для всех х, не равных х0 и удовлетворяющих условию |x – x0| < δ, выполняется неравенство |f(x) – A| < ε. (2)
или f(x) → А при х → х0. С помощью логических символов определение можно записать в виде
Смысл определения состоит в том, что для всех значений х, достаточно близких к х0 , значения f(x) как угодно мало отличаются от числа А (по абсолютной величине). Рассмотрим геометрический смысл предела функции в точке. Неравенство |f(x) – A| < ε равносильно двойному неравенству A- ε < f(x) < A+ ε, соответствующему расположению части графика в полосе шириной 2ε. Аналогично неравенство |x – х0| < δ равносильно двойному неравенству х0- δ < x < х0+ δ , соответствующему попаданию точек х в δ-окрестность точки х0.
Итак, число А есть предел функции y = f(x) при х → х0 , если для любого числа ε > 0 найдется такая δ-окрестность точки х0, что для всех х ≠ х0 из этой окрестности соответствующие ординаты графика функции f(x) будут заключены в полосе A- ε < у < A+ ε, какой бы узкой эта полоса не была. Замечание 1. Определение предела не требует существования функции в самой точке х0. Другими словами, рассматривая предел функции в точке х0, предполагается, что х стремится к х0, но не достигает значения х0. Поэтому наличие или отсутствие предела при х → х0 не связано со значением функции (или его отсутствием) в самой точке х0 .
Очевидно, что определение этих пределов будет аналогично рассмотренному выше при х → х0, если вместо значений х, удовлетворяющих условию |x – x0| < δ, при которых выполняется неравенство (2), рассматривать значения х такие, что x0-δ < x < x0 при х → х0 - 0 (слева), или значения х такие, что x0 < x < x0 +δ при х → х0 + 0 (справа). Разумеется, если
Свойства пределов. 1. Если предел функции существует, то он единствен; Обозначим А = 2. 3. В частности, постоянный множитель можно выносить за знак предела
4. 5. Если
6. Если в некоторой окрестности точки х0 (или при достаточно больших х) f(x) ≤ g(x), то
Определение. Функция f(x) называется бесконечно малой (б.м.) в окрестности точки х0, если Определение. Функция f(x) называется бесконечно большой (б.б.) в окрестности точки х0, если Определение. Функция f(x) называется ограниченной в окрестности точки х0, если
Свойства б.м. и б.м. величин. 1) Произведение б.м. величины на ограниченную функцию есть б.м.; 2) Отношение ограниченной функции к б.м. величине есть б.б. величина; 3) Произведение б.б. величины на функцию, предел которой отличен от нуля, есть б.б. величина; 4) Отношение ограниченной функции к б.б. величине есть б.м. величина.
Определение. Две б.м. величины α1(х) и α2(х) называются эквивалентными (обозначение α1(х) ~ α2(х)) в окрестности точки х0, если предел их отношения равен единице, т. е.
Это означает, что эквивалентные б.м. величины взаимозаменяемы при вычислении пределов.
Поиск по сайту: |


 Выясним геометрический смысл предела функции в бесконечности. Неравенство |f(x) – A| < ε равносильно двойному неравенству A- ε < f(x) < A+ ε, соответствующему расположению части графика в полосе шириной 2ε.
Выясним геометрический смысл предела функции в бесконечности. Неравенство |f(x) – A| < ε равносильно двойному неравенству A- ε < f(x) < A+ ε, соответствующему расположению части графика в полосе шириной 2ε.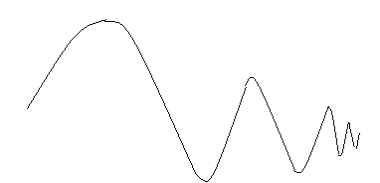

 Этот предел функции обозначается
Этот предел функции обозначается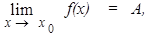


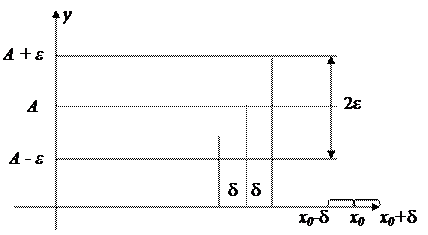

 Замечание 2. Если при стремлении х к х0 переменная х принимает лишь значения, меньшие х0, или, наоборот, лишь значения, большие х0, и при этом функция f(x) стремится к некоторому числу А, то говорят об односторонних пределах функции f(x), левостороннем и правостороннем:
Замечание 2. Если при стремлении х к х0 переменная х принимает лишь значения, меньшие х0, или, наоборот, лишь значения, большие х0, и при этом функция f(x) стремится к некоторому числу А, то говорят об односторонних пределах функции f(x), левостороннем и правостороннем:


 и В =
и В = 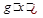 . Тогда
. Тогда А + В;
А + В;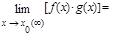 А ∙ В.
А ∙ В. С∙ А;
С∙ А;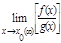 =
=  ;
; = А, и
= А, и 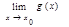 = и0, то предел сложной функции
= и0, то предел сложной функции = А.
= А. ≤
≤  .
. = 0.
= 0. для всех х из этой окрестности.
для всех х из этой окрестности.