 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
По выполнению контрольной работы по линейной алгебреСтр 1 из 2Следующая ⇒
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Малаховский Н.В. Методические указания и контрольные задания Для студентов заочного отделения по дисциплине «Линейная алгебра» Калининград, 2012 Пояснительная записка
Целями и задачами дисциплины «Линейная алгебра» являютсянакопление необходимого запаса сведений по математике, а также освоение математического аппарата, помогающего моделировать, анализировать и решать экономические задачи, помощь в усвоении математических методов, дающих возможность изучать и прогнозировать процессы и явления из области будущей деятельности студентов; развитие логического и алгоритмического мышления, способствование формированию умений и навыков самостоятельного анализа исследования экономических проблем, развитию стремления к научному поиску путей совершенствования своей работы. Дисциплина «Линейная алгебра» является предшествующей для следующих дисциплин: математический анализ, теория вероятностей м математическая статистика, методы оптимальных решений, информатика, математические методы и модели, микроэкономика, макроэкономика, статистика, эконометрика. Процесс изучения дисциплины направлен на формирование следующих компетенций: В результате изучения этой дисциплины студент должен: знать: основы линейной алгебры, необходимые для решения экономических задач, уметь применять методы математического анализа и моделирования, теоретического и экспериментального исследования для решения экономических задач, ладеть навыками применения современного математического инструментария для решения экономических задач; методикой построения, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений и процессов. Фундаментальность подготовки в области математики включает в себя достаточную общность математических понятий и конструкций, обеспечивающую широкий спектр их применимости, точность формулировок математических свойств изучаемых объектов, логическую строгость изложения математики, опирающуюся на адекватный современный математический язык. В ходе изучения дисциплины “Линейная алгебра” основное внимание уделяется изучению основных понятий и методов линейной алгебры, а также роли и месту линейной алгебры в решении различных экономических задач. Практическая часть дисциплины предназначена для выработки у студентов логического и аналитического мышления, формирования вычислительных навыков, умения проводить приближенные расчеты, привития первичных навыков работы с наиболее популярными прикладными программами. Методические указания по выполнению контрольной работы по линейной алгебре Прямоугольная таблица чисел вида
называется матрицей.Числа, из которых состоит матрица, называются ееэлементами. Элементы матрицы нумеруются двумя индексами, первый из которых обозначает номер строки, а второй- номер столбца.Число строк и столбцов матрицы называется ее порядком : Для матриц определены следующие линейные операции: сложение, умножение матрицы на число, умножение матриц. Складываются матрицы поэлементно, поэтому можно найти сумму только матриц одинакового порядка. При умножении матрицы на действительное число каждый элемент этой матрицы умножается на это число. Произведениемматрицы А порядка
Следует обратить внимание, что умножить можно только те матрицы, в которых число столбцов в первой матрице равно числу строк во второй матрице. Также следует иметь в виду, что в общем случае умножение матриц не коммутативно: Определителем квадратной матрицы А называется число detA , поставленное в соответствие этой матрице по определенному закону. Для квадратных матриц второго порядка: Определители более высоких порядков можно вычислить согласно теореме: Теорема.Определитель квадратной матрицы А порядка n равен сумме произведений элементов некоторой строки (или столбца) матрицы на их алгебраические дополнения:
где Обратной матрицей к квадратной матрице А называется такая матрица Теорема.Если
Следует обратить внимание на расположение алгебраических дополнений в обратной матрице. Рангом матрицы называется наибольший порядок ее отличного от нуля минора (или число линейно независимых строк или столбцов матрицы). Минором порядка k произвольной матрицы А называется определитель, составленный из элементов матрицы А, стоящих на пересечении любых ее k строк и k столбцов. Существуют два метода нахождения ранга матрицы: метод окаймляющих миноров (состоящий в последовательном вычислении миноров с первого порядка и до тех пор, пока это возможно, либо пока все миноры порядка k+1 не окажутся =0, тогда rangA=k), либо метод элементарных преобразований (матрица приводится к ступенчатому виду, и тогда ранг равен числу ненулевых строк матрицы). Системой m линейных алгебраических уравнений (СЛАУ) с n неизвестными называется система вида
Система называется совместной, если существует хотя бы одно ее решение, то есть если найдется такой набор чисел, что при подстановке этих чисел вместо соответствующих переменных, каждое уравнение системы обращается в тождество. Возможны три случая: - система имеет единственное решение; - система имеет бесконечно много решений. Теорема Кронекера- Капелли.Система линейных уравнений совместна тогда и только тогда, когда ранги ее основной и расширенной матриц равны. Основной матрицей системы называется матрица ее коэффициентов, расширенной- матрица, включающая помимо коэффициентов столбец свободных членов. Существуют три основных метода решения СЛАУ. 1)Матричный метод, основанный на матричной записи системы 2) Метод Крамера, заключается в вычислении основного определителя системы 3) Метод Гаусса,или метод последовательного исключения переменных. Система уравнений, а точнее, ее расширенная матрица путем элементарных преобразований (замена уравнений местами, умножение уравнения на число, прибавление к одному уравнению системы другого, умноженного на некоторое число) приводится к ступенчатому виду. Далее из каждого уравнения, начиная с последнего, выражается соответствующая переменная. Метод Гаусса - самый универсальный из предложенных, позволяет решать практически все системы. Однородные системы линейных алгебраических уравнений- это системы, в которых столбец свободных членов равен 0. Однородная система уравнений совместна всегда, так как она имеет нулевое решение. Теорема.Однородная СЛАУ имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных. Система решений называется фундаментальной, если любое решение СЛАУ выражается в виде ее линейной комбинации.
Поиск по сайту: |
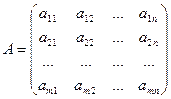
 . Матрица, число строк и столбцов которой совпадает, называется квадратной.
. Матрица, число строк и столбцов которой совпадает, называется квадратной. на матрицу В порядка
на матрицу В порядка  называется матрица С порядка
называется матрица С порядка  представляет собой сумму произведений элементов i-той строки матрицы А на соответствующие элементы j-го столбца матрицы В:
представляет собой сумму произведений элементов i-той строки матрицы А на соответствующие элементы j-го столбца матрицы В: .
. .
. .
. ,
, - алгебраическое дополнениеэлемента
- алгебраическое дополнениеэлемента  матрицы А, а
матрицы А, а 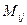 - минор этого элемента, то есть определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием j–го столбца и i-той строки.
- минор этого элемента, то есть определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием j–го столбца и i-той строки. , что
, что  , где
, где 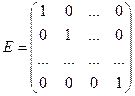 - единичная матрица соответствующего порядка.
- единичная матрица соответствующего порядка. , то
, то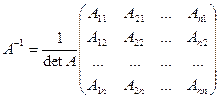 .
.
 -действительные числа, называемые свободными членами.
-действительные числа, называемые свободными членами. . Вектор-столбец решения находится как
. Вектор-столбец решения находится как  . Ввиду громоздкости вычислений применяется в основном в теории.
. Ввиду громоздкости вычислений применяется в основном в теории. и определителей
и определителей  , в которых i-тый столбец заменен столбцом свободных членов. Решение системы в этом случае :
, в которых i-тый столбец заменен столбцом свободных членов. Решение системы в этом случае :  .
.