 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел функции в точке и бесконечностиСтр 1 из 2Следующая ⇒
Тема 5. Пределы. Предел функции (и числовой последовательности как функции натурального аргумента) – одно из фундаментальных понятий «математического анализа и линейной алгебры». Оно лежит в основе таких понятий как бесконечно малая и бесконечно большая величины, и являются для студентов наиболее сложным для понимания и использования. Цельлекции состоит в умении четко разобраться с определениями предела в различных формах, т.к. понимание понятия предела и умение пользоваться этим понятием лежит в основе доказательств признаков существования пределов функций, основных теоремах о пределах. Задачалекции заключается в умении пользоваться теоремами о пределах. Главная задача- уметь разобраться с вычислениями пределов в условиях неопределенностей, а также использовать понятие пределов функции при исследовании функции на непрерывность.
5.1. Предел числовой последовательности. Простейшие свойства пределов (единственность предел, переход к пределам в неравенствах). 5.2. Предел функции в точке и в бесконечности. 5.3.Бесконечно малые величины и их свойства. Бесконечно большие величины. 5.4.Основные теоремы о пределах. Признаки существования пределов. 5.5.Второй замечательный предел. Число «е». Понятие о натуральных логарифмах. 5.6. Непрерывность функции в точке и на промежутке. Основные теоремы о непрерывных функциях.
Предел числовой последовательности.
Иными словами, числовая последовательность- это функция натурального аргумента Примеры. 1. 2. 3. 4. 5. Изобразим последовательность (пример 5) на числовой прямой (рис.5.1.2)
Рис. 5.1.2
Определение.Число аназывается пределом числовой последовательности , выполняется неравенство В этом случае записывают:
Если последовательность имеет предел, она называется сходящейся,в противном случае - расходящейся. Для пределов числовой последовательности имеют место следующие теоремы (свойства). Теорема 5.1.1. Если последовательность Доказательство.Пусть Пусть выбранные окрестности не пересекаются.
а-
Рис.5.1.2
Если N=max
Теорема 5.1.2. Предел постоянной величины равен самой постоянной.
Если считать, что
Теорема 5.1.3. Предел положительной последовательности (переменной) неотрицательный; предел отрицательной последовательности (переменной) не положителен.
Доказательство. а) Пусть при
б) Если
Теорема 5.1.4. Если
Доказательство.Если
b-
Рис.5.1.4 Если окрестности не пересекаются (всегда можно их выбрать такими), то для n>N =max Замечание. Из теорем 5.1.3 и 5.1.4 следует: при переходе к пределам в неравенствах знак неравенства сохраняется.
Предел функции в точке и бесконечности.
С понятием предела числовой последовательности
В этом случае записывают:
0 М х Рис.5.2.1
С помощью логических символов определение можно записать следующим
образом:
Геометрически это же определение означает: как только Пример. Доказать, что Пусть
Замечание. Приведенное определение предела функции подразумевает под высказыванием
Пусть функция
В этом случае записывают: С помощью логических символов равенства (5.1) (или определение предела функции) запишется:
Рассмотрим геометрический смысл предела функции.
0 а-δ а х а+δ х
Рис.5.2.2
Совместное выполнение неравенств (5.2.2) означает: ЧислоА является пределом функции
Замечание. Т.к. предел рассматривается при значениях
Поиск по сайту: |
 Определение. Если каждому натуральному числу n по некоторому закону поставлено в соответствие определенное число
Определение. Если каждому натуральному числу n по некоторому закону поставлено в соответствие определенное число  , то говорят, что числа
, то говорят, что числа  :
: 
 , числа
, числа 
 - монотонно убывающая и ограниченная;
- монотонно убывающая и ограниченная; : 2,
: 2,  ,
,  ,…,
,…,  ,…- монотонно возрастающая и неограниченная;
,…- монотонно возрастающая и неограниченная; -1, 1, -1, 1…- немонотонная и ограниченная;
-1, 1, -1, 1…- немонотонная и ограниченная; -1,
-1,  , -
, -  ,
, 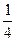 ,…- немонотонная и ограниченная;
,…- немонотонная и ограниченная; 0,
0,  ,
,  ,
,  ,
,  ,
,  ,
,  ,…
,…
 На рис.5.1.2 видно, сто с ростомn члены последовательности приближаются к единице,т.е. величина
На рис.5.1.2 видно, сто с ростомn члены последовательности приближаются к единице,т.е. величина  становятся все меньше и меньше. Иными словами, если рассмотреть любую сколь угодно малую окрестность числа а=1, в этой окрестности накапливается бесчисленное множество членов последовательности
становятся все меньше и меньше. Иными словами, если рассмотреть любую сколь угодно малую окрестность числа а=1, в этой окрестности накапливается бесчисленное множество членов последовательности 
 , начиная с некоторого номера N.
, начиная с некоторого номера N. , найдется такой номер N(зависящий от
, найдется такой номер N(зависящий от  <
<


 >0
>0 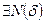 , n>N
, n>N
 <
< 
 . По условию для
. По условию для  >0
>0  ,
,  <
<  по предположению для
по предположению для  >0
>0  n>
n> 
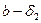 <
< 
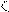







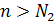

 а а+
а а+  b
b  ,то для n> N один и тот же член одновременно находится в двух разных окрестностях. Следовательно, если
,то для n> N один и тот же член одновременно находится в двух разных окрестностях. Следовательно, если  ,
,  ,…,
,…,  , то, начиная уже с первого члена последовательности (n≥1), все члены последовательности лежат в окрестности точки С (совпадают с числом С), т.е.
, то, начиная уже с первого члена последовательности (n≥1), все члены последовательности лежат в окрестности точки С (совпадают с числом С), т.е.  .
.

 . Предположим, что а<0. по определению предела для
. Предположим, что а<0. по определению предела для  , что для n>N
, что для n>N  .
.



 а-δ а
а-δ а  <0, доказательство аналогично.
<0, доказательство аналогично.
 и
и 

 , n>
, n>  выполняется условие
выполняется условие 
 , такой, что для n>
, такой, что для n> 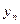 <
< 







 n>
n> 
 b b+
b b+  .
. в бесконечности. Здесь аргумент х, изменяясь, может принимать различные значения.
в бесконечности. Здесь аргумент х, изменяясь, может принимать различные значения. Определение.ЧислоА называется пределом функции y=f(x) при х, стремящимся к бесконечности, если для любого, сколь угодно малого положительного числа
Определение.ЧислоА называется пределом функции y=f(x) при х, стремящимся к бесконечности, если для любого, сколь угодно малого положительного числа  , найдется такое положительное число М>0 (зависящее от
, найдется такое положительное число М>0 (зависящее от  >M верно неравенство
>M верно неравенство  <
< 
 у
у


 А+ε
А+ε






 А
А
 А-ε
А-ε
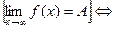
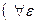 >0) (
>0) ( 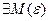 ) (
) (  >M)
>M)  <f(x)<
<f(x)<  , какой бы узкой ни была эта полоса (рис.5.2.1)
, какой бы узкой ни была эта полоса (рис.5.2.1)
 . Найдем такое М>0, чтобы
. Найдем такое М>0, чтобы  <
<  <
< 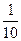
 <
< 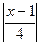 >10 х>41; М=41. если х>41 выполняется условие
>10 х>41; М=41. если х>41 выполняется условие 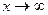 , что
, что  . Но т.к. возможны случаи
. Но т.к. возможны случаи  или
или  , то для
, то для  Определение.Число А называется пределом функции
Определение.Число А называется пределом функции  , что для всех х не равных а и удовлетворяющих условию x – a δ выполняется условие
, что для всех х не равных а и удовлетворяющих условию x – a δ выполняется условие  < ε
< ε  . (5.2.1)
. (5.2.1) >0) (
>0) ( 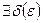 >0) (
>0) (  <
<  y
y




















 А+ε
А+ε



 А 2ε
А 2ε










 <
< 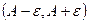 (шириной 2
(шириной 2  (но
(но  ), то поведение функции в самой точке а в данном случае не представляет интереса.
), то поведение функции в самой точке а в данном случае не представляет интереса.