 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Колебания материальной точки
1.5.1. Свободные колебания.В случае, когда действующая на материальную точку позиционная сила стремиться вернуть ее в исходное положение, движение точки будет носить колебательный характер. Такую силу принято называть восстанавливающей. Пусть материальная точка может двигаться по известной траектории под действием восстанавливающей силы, структура которой имеет вид
Перепишем уравнение в виде
Это линейное однородное дифференциальное уравнение второго порядка. Предположим, что его решение должно иметь вид Для проверки правильности предположения найдем выражение для
Полученное произведение равно нулю, если
Если известны, например, начальные условия движения (
позволяют найти Таким образом, под действием восстанавливающей силы материальная точка совершает движение по синусоидальному закону, т.е. гармоническое колебательное движение. Эти колебания называют свободными; наибольшее отклонение Заметим, что если начало отсчета координаты В частном случае, когда траектория точки – прямая линия, касательная и траектория совпадают; а ПРИМЕР 1.7. В результате воздушного взрыва корабль получил вертикальную скорость РЕШЕНИЕ. Обозначим вертикальное перемещение корабля
Запишем дифференциальное уравнение вертикальных колебаний корабля, спроецировав на вертикаль силы, на него действующие (сила веса и архимедова сила поддержания): где При записи уравнения учтено, что в равновесном положении водоизмещение корабля и сила поддержания равны и противоположно направлены. Приведем полученное уравнение к виду (1.29)
Тогда период вертикальных колебаний будет Система уравнений (1.32) позволяет найти амплитуду и начальную фазу вертикальных колебаний как
1.5.2. Свободные колебания при сухом трении.Обсудим влияние сухого трения в ходе решения задачи о движении груза массы
Нанесем на рисунок силы, действующие на груз при его движении в положительном направлении оси
и приведем его к виду Это неоднородное дифференциальное уравнение второго порядка, решение которого есть сумма решений однородного уравнения (1.29) и частного решения. Последнее находится достаточно просто, если предположить, что его величина постоянна и равна Тогда общее решение неоднородного уравнения запишется как Заметим, что полученное решение справедливо только при совпадении направлений перемещения и скорости точки (при Окончательно имеем:
Зависимость перемещения груза от времени изображена на рис.1.13.
В настоящем пособии ограничимся обсуждением приведенного результата (с подробным решением задачи можно ознакомиться, например, в [1]). Хотя движение, описываемое формулами (1.34), строго говоря, не является периодическим (так как с течением времени максимальные отклонения точки от положения равновесия уменьшаются), в механике такое движение принято называть затухающими колебаниями. Заметим, что, во-первых, анализируемое движение должно рассматриваться как последовательность этапов, в пределах каждого из которых величина скорости точки сохраняет свой знак; время, положение и скорость в конце предыдущего этапа оказываются начальными условиями для последующего этапа. В результате период затухающих колебаний Во-вторых, движение точки заканчивается в тот момент, когда ее максимальное отклонение (при этом скорость точки равна нулю) оказывается в зоне, называемой зоной нечувствительности. Ширина зоны определяется величиной силы сухого трения (в этой зоне сила упругости пружины оказывается меньше силы сухого трения, т.е.
1.5.3. Свободные колебания при линейно – вязком сопротивлении.Рассмотрим движение материальной точки под действием восстанавливающей силы и силы сопротивления
и приведем его к виду
Предположим, что его решение должно иметь вид
Для проверки правильности предположения найдем выражения для
Полученное произведение равно нулю, если 1. Пусть
Характер движения в этом случае представлен на рис.1.14; движение является апериодическим, эспоненциальным, что говорит о большом сопротивлении.
2. Пусть Характер движения аналогичен представленному на рис.1.14. 3. Пусть
Характер движения - затухающие колебания, - представлен на рис.1.15.
Период затухающих колебаний
несколько больше периода свободных колебаний, а последовательность амплитуд представляет в этом случае убывающую геометрическую прогрессию, знаменатель которой называется декрементом колебаний. Его величина будет
В некоторых задачах используется модуль его натурального логарифма; он называется логарифмическим декрементом колебаний В тех случаях, когда сила сопротивления пропорциональна скорости в степени выше первой (например, Иногда на практике приходится иметь дело с обратной задачей, когда по записи процесса колебательного движения необходимо сделать вывод о структуре силы сопротивления. Алгоритм действий следующий: во-первых, измеряются интервалы времени между наибольшими отклонениями. Если интервалы одинаковы, то сила сопротивления является либо силой сухого трения, либо силой линейно – вязкого сопротивления. Во-вторых, измеряются наибольшие отклонения от средней линии; если они образуют арифметическую прогрессию, преобладает сухое трение, а если геометрическую, то линейно-вязкое. В противном случае действует сила сопротивления, пропорциональная скорости точки в степени выше первой. ПРИМЕР 1.8. (задача 32.64 из [2]). Для определения вязкости жидкости Кулон употреблял следующий метод: подвесив на пружине тонкую пластинку А, он заставлял ее колебаться сначала в воздухе, а затем в той жидкости, вязкость которой надлежало определить, и находил продолжительность одного размаха: РЕШЕНИЕ. Изобразим на рис.1.16 пластинку в сосуде с жидкостью и нанесем силы, на нее действующие.
Если начало координаты При колебаниях в воздухе сила Возведем в квадрат выражение для периода
После несложных преобразований получим 1.5.4. Вынужденные колебания материальной точки при действии гармонического возбуждения. В некоторых случаях кроме восстанавливающей силы может дополнительно действовать возмущающая сила (является заданной функцией времени) либо кинематическое возбуждение (движение точки подвеса по заданному закону); последнее, согласно (1.25), может быть учтено добавлением силы инерции переносного движения. Рассмотрим наиболее распространенный случай, когда возмущающая сила изменяется по гармоническому закону, т.е. Дифференциальное уравнение в этом случае будет
Оно может быть переписано в виде
Это неоднородное дифференциальное уравнение второго порядка, решение которого есть сумма решений однородного уравнения (1.29) и частного решения. В случае, когда Тогда общее решение неоднородного уравнения запишется как Как уже говорилось выше, постоянные интегрирования Остановимся подробнее на втором слагаемом, описывающем не зависящие от начальных условий вынужденные колебания (в технических приложениях эти колебания называют вибрацией). Введем величину
Анализ амплитудно-частотной характеристики показывает, что при стремлении частоты вынуждающей силы к нулю, амплитуда вибрации стремится к величине статического отклонения; при бесконечно большой частоте вынуждающей силы амплитуда вибрации стремится к нулю; при совпадении частоты вибрации и собственной частоты амплитуда вибрации может стать бесконечно большой (явление резонанса). Анализ фазово-частотной характеристики показывает, что смещение и вынуждающая сила до резонанса совпадают по направлению; после резонанса их направления противоположны. Явление резонанса. Рассмотрим более подробно ситуацию, когда
Отсюда
График этой зависимости (при нулевых начальных условиях) приведен на рис.1.18.
Как видно, при Явление биений. В случае, когда частота Опуская выкладки (при желании с ними можно ознакомиться, например, в [1]), для вибрации получаем зависимость
График этого движения представлен на рис.1.19.
Показанные здесь биения представляют собой колебания, происходящие с частотой Кинематическое возбуждение. Как было сказано выше, кинематическое возбуждение колебаний (например, гармонические колебания Выражение для коэффициента динамичности для этого случая примет вид
Амплитудно-частотная и фазово-частотная характеристики движения в этом случае приведены на рис.1.20а и 1.20.б соответственно.
Очевидно, что при ПРИМЕР 1.9. Виброметр используется для определения амплитуд вертикальных колебаний одной из частей машины. В подвижной системе прибора демпфер отсутствует. Собственная частота колебаний виброметра – 6 Гц. В каком диапазоне должна находиться частота вибрации, чтобы погрешность измерения ее амплитуды не превышала 5%? РЕШЕНИЕ. Очевидно, что в рассматриваемом примере имеет место кинематическое возбуждение колебаний. Из рис.1.20.а и формулы (1.47) видно, что при Очевидно, что в таком случае показания виброметра будут наиболее точно регистрировать колебания объекта, на котором он установлен; при этом кинематическое возбуждение и относительное движение груза будут в противофазе (т.е. Воспользуемся формулой (1.47) для расчета амплитуды вибрации и выразим из нее отношение Тогда на границе искомого диапазона должно выполняться равенство
Выполнив расчет, получим, что
Из графика 1.20.а видно, что и в дорезонансной области существуют частоты вибрации, где соотношение
выполняется, однако конструировать виброметр для работы в столь узком диапазоне частот не имеет смысла. Действие полигармонического или периодического возбуждения.В случае, когда вынуждающая сила представляет собой полигармоничекое воздействие (например, В случае, когда вынуждающая сила оказывается периодической функцией, можно попробовать разложить ее в тригонометрический ряд Фурье. Если в результате разложения можно ограничиться учетом действия нескольких членов ряда (амплитудные значения остальных членов ряда существенно меньше оставленных, а частоты не совпадают с частой свободных колебаний, т.е. резонансные явления отсутствуют), воздействие, с достаточной степенью точности, полагают полигармоническим. В противном случае можно воспользоваться определением периодического решения в замкнутой форме. В ограниченных рамках настоящего пособия этот материал не приводится, однако ознакомиться с ним можно, например, в [1].
1.5.5. Влияние сопротивления на вынужденные колебания. Рассмотрим движение материальной точки вдоль оси
Оно может быть переписано в виде
где Это неоднородное дифференциальное уравнение второго порядка, решение которого есть сумма решений однородного уравнения (1.40) и частного решения. В случае, когда
Тогда общее решение неоднородного уравнения запишется как где Через некоторый промежуток времени (из-за сопротивления) остается только последнее слагаемое (вибрация); при этом перемещение точки сдвинуто по фазе относительно вынуждающей силы на угол На рис.1.20 приведены амплитудно-частотная и фазово-частотная характеристики этого движения.
Отметим несколько особенностей: наличие сопротивления делает амплитуду вибрации при резонансе конечной; с ростом сопротивления величина амплитуды уменьшается (уже при значении
Вопросы и задачи для самоконтроля 1. Какие модели используются в классической механике для пространства, времени, объектов и их взаимодействия? 2. Что такое структура силы? Приведите примеры наиболее часто встречающихся структур сил. 3. Сформулируйте законы классической механики. В каких системах отсчета они справедливы? Какая система отсчета называется инерциальной? 4. Запишите проекции основного закона классической механики на оси декартовой координатной системы (на оси естественной координатной системы, на оси цилиндрической координатной системы). 5. Достаточно ли знания структуры силы, действующей на точку известной массы, чтобы найти закон ее движения? 6. Можно ли судить о структуре силы, действующей на точку заданной массы, если известны ее траектория и закон движения по ней? 7. Чем отличаются дифференциальные уравнения движения материальной точки в инерциальной и неинерциальной системах отсчета? 8. Запишите условие покоя материальной точки в неинерциальной системе отсчета. 9. Почему частоту свободных колебаний иногда называют собственной частотой? 10. Как выглядит график зависимости координаты (отклонение от положения статического равновесия) от времени при наличии сухого трения? Какую прогрессию образуют амплитуды этих колебаний? Чем обусловлено наличие зоны нечувствительности? 11. Какие типы движения могут иметь место, если кроме восстанавливающей силы на материальную точку действует сила линейно – вязкого сопротивления? 12. Расскажите о явлениях биений и резонансе. 13. Как влияет линейно – вязкое сопротивление на амплитуду вибрации? 14. Что такое кинематическое возбуждение колебаний? В чем отличие амплитудно – частотных характеристик при кинематическом и силовом возбуждениях? 15. Решите следующие задачи из [2] : 26.5; 26.13; 27.5; 27.9; 27.33; 27.18; 27.21; 32.26; 32.62; 32.81; 33.2; 33.14.
Поиск по сайту: |
 ; здесь
; здесь  - проекция силы на касательную к траектории,
- проекция силы на касательную к траектории, 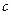 - известный коэффициент пропорциональности, а
- известный коэффициент пропорциональности, а 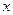 - криволинейная координата, являющаяся отклонением точки от начального положения. Тогда дифференциальное уравнение движения материальной точки вдоль траектории будет
- криволинейная координата, являющаяся отклонением точки от начального положения. Тогда дифференциальное уравнение движения материальной точки вдоль траектории будет .
.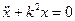 , где
, где  . (1.29)
. (1.29) . (1.30)
. (1.30) и подставим его и (1.30) в (1.29). Вынося общий множитель за скобку, имеем
и подставим его и (1.30) в (1.29). Вынося общий множитель за скобку, имеем .
. . Это означает, что предположение (1.30) справедливо, а решение уравнения (1.29) имеет вид
. Это означает, что предположение (1.30) справедливо, а решение уравнения (1.29) имеет вид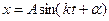 , где
, где  . (1.31)
. (1.31)
 - начальное положение,
- начальное положение,  - начальная скорость), для определения постоянных величин
- начальная скорость), для определения постоянных величин  и
и 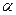 начальные условия следует подставить в выражениях для
начальные условия следует подставить в выражениях для  . Полученные уравнения
. Полученные уравнения

 и
и  . (1.32)
. (1.32) - фазой, а
- фазой, а  называется круговой (или циклической) частотой колебаний; она определяет число колебаний, совершаемых точкой за
называется круговой (или циклической) частотой колебаний; она определяет число колебаний, совершаемых точкой за 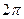 секунд (здесь
секунд (здесь  - период колебаний). Заметим, что частота
- период колебаний). Заметим, что частота  зависит только от массы точки
зависит только от массы точки 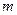 и коэффициента пропорциональности
и коэффициента пропорциональности  . Найти период и амплитуду вертикальной качки корабля, если известны площадь его ватерлинии
. Найти период и амплитуду вертикальной качки корабля, если известны площадь его ватерлинии  , водоизмещение
, водоизмещение  и присоединенная масса жидкости в вертикальном направлении
и присоединенная масса жидкости в вертикальном направлении  . Развалом бортов и сопротивлением воды пренебречь.
. Развалом бортов и сопротивлением воды пренебречь.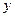 (см.рис.1.11).
(см.рис.1.11).
 ;
; - удельный вес воды,
- удельный вес воды,  - объем подводной части корабля в равновесном состоянии.
- объем подводной части корабля в равновесном состоянии. , здесь
, здесь 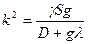 .
. 
 .
.
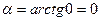 .
. для которой задан; груз присоединен к стене пружиной длины
для которой задан; груз присоединен к стене пружиной длины  и жесткости
и жесткости 
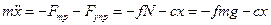
 . (1.33)
. (1.33) . После подстановки
. После подстановки  .
. .
. либо
либо  ). При движении материальной точки в противоположном направлении (например,
). При движении материальной точки в противоположном направлении (например,  ), сила трения изменит направление на противоположное (
), сила трения изменит направление на противоположное (  на рис.1.12), что приведет к изменению знака правой части дифференциального уравнения и, как следствие, знака частного решения.
на рис.1.12), что приведет к изменению знака правой части дифференциального уравнения и, как следствие, знака частного решения. ;
; при
при  . (1.34)
. (1.34)
 равен периоду свободных колебаний, а амплитуды колебаний образуют арифметическую прогрессию, т.е.
равен периоду свободных колебаний, а амплитуды колебаний образуют арифметическую прогрессию, т.е.  . (1.35)
. (1.35) , и точка не может продолжить свое движение).
, и точка не может продолжить свое движение).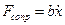 , пропорциональной скорости точки. Составим дифференциальное уравнение движения
, пропорциональной скорости точки. Составим дифференциальное уравнение движения
 , где
, где  . (1.36)
. (1.36)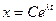 . (1.37)
. (1.37) и подставим их и (1.37) в (1.36). Вынося общий множитель за скобку, имеем
и подставим их и (1.37) в (1.36). Вынося общий множитель за скобку, имеем .
. . Это означает, что сделанное предположение (1.37) справедливо. Однако характер движения будет зависеть от соотношения величин
. Это означает, что сделанное предположение (1.37) справедливо. Однако характер движения будет зависеть от соотношения величин 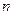 и
и  . Тогда
. Тогда  - действительные отрицательные числа и решение будет иметь вид
- действительные отрицательные числа и решение будет иметь вид . (1.38)
. (1.38)
 . Тогда
. Тогда  - действительные отрицательные числа и решение будет иметь вид
- действительные отрицательные числа и решение будет иметь вид  . (1.39)
. (1.39) . Тогда
. Тогда  - комплексные числа и решение может быть приведено к виду
- комплексные числа и решение может быть приведено к виду
 . (1.40)
. (1.40)
 (1.41)
(1.41) . (1.42)
. (1.42) .
. ), дифференциальное уравнение нелинейно, а его решение не может быть записано в виде аналитической зависимости. По результатам численного решения такого уравнения строится график (при большом сопротивлении график похож на рис.1.14; при малом – на рис.1.15, однако интервалы времени между наибольшими отклонениями и отношения соседних отклонений не будут постоянны).
), дифференциальное уравнение нелинейно, а его решение не может быть записано в виде аналитической зависимости. По результатам численного решения такого уравнения строится график (при большом сопротивлении график похож на рис.1.14; при малом – на рис.1.15, однако интервалы времени между наибольшими отклонениями и отношения соседних отклонений не будут постоянны).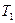 - в первом случае и
- в первом случае и  - во втором. Сила трения между пластинкой и жидкостью может быть выражена формулой
- во втором. Сила трения между пластинкой и жидкостью может быть выражена формулой  , где
, где 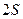 - площадь пластинки,
- площадь пластинки,  - ее скорость,
- ее скорость, 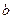 - коэффициент вязкости. Пренебрегая трением между пластинкой и воздухом, определить коэффициент
- коэффициент вязкости. Пренебрегая трением между пластинкой и воздухом, определить коэффициент 
 . Тогда получим выражение
. Тогда получим выражение , где
, где  .
. .
. .
. .
. , где
, где 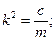
 . (1.43)
. (1.43) , последнее находится достаточно просто, если предположить, что его вид
, последнее находится достаточно просто, если предположить, что его вид  , где
, где  .
. . (1.44)
. (1.44) .
. , представляющую смещение точки при действии на нее постоянной силы
, представляющую смещение точки при действии на нее постоянной силы  . Величина отношения амплитуды
. Величина отношения амплитуды  ; эта величина называется коэффициентом динамичности
; эта величина называется коэффициентом динамичности  . Зависимость модуля коэффициента динамичности от отношения
. Зависимость модуля коэффициента динамичности от отношения  называется амплитудно-частотной характеристикой, а зависимость отставания смещения от вынуждающей силы – фазово-частотной характеристикой. Эти характеристики приведены на рис.1.17.а и 1.17.б соответственно.
называется амплитудно-частотной характеристикой, а зависимость отставания смещения от вынуждающей силы – фазово-частотной характеристикой. Эти характеристики приведены на рис.1.17.а и 1.17.б соответственно.
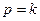 . Частное решение уравнения (1.43) в этом случае следует искать в виде
. Частное решение уравнения (1.43) в этом случае следует искать в виде  . Подставив это предположение в (1.43), получаем два соотношения
. Подставив это предположение в (1.43), получаем два соотношения
 .
. ,
,  . Окончательно получим
. Окончательно получим . (1.45)
. (1.45)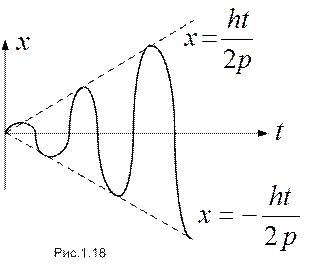
 . (1.46)
. (1.46)
 конца пружины жесткости
конца пружины жесткости  .
. . (1.47)
. (1.47)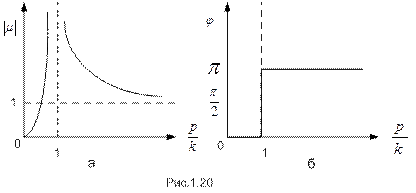
 вынужденные колебания отсутствуют; с ростом частоты кинематического возбуждения амплитуда вибрации растет, пока не достигнет области резонанса; при дальнейшем возрастании частоты кинематического возбуждения амплитуда вынужденных колебаний стремиться к амплитуде кинематического возбуждения, при этом кинематическое возбуждение и вибрация происходят в противофазе (т.е.
вынужденные колебания отсутствуют; с ростом частоты кинематического возбуждения амплитуда вибрации растет, пока не достигнет области резонанса; при дальнейшем возрастании частоты кинематического возбуждения амплитуда вынужденных колебаний стремиться к амплитуде кинематического возбуждения, при этом кинематическое возбуждение и вибрация происходят в противофазе (т.е.  ).
). амплитуда вибрации стремиться к амплитуде кинематического возбуждения.
амплитуда вибрации стремиться к амплитуде кинематического возбуждения. . Потребуем, чтобы величина этого отношения отличалась от 1 (их точное совпадение) не более, чем на 5%, т.е. была бы равна 1.05.
. Потребуем, чтобы величина этого отношения отличалась от 1 (их точное совпадение) не более, чем на 5%, т.е. была бы равна 1.05.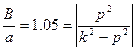 .
.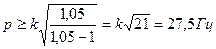 .
.
 ;
;  .
. , силы линейно – вязкого сопротивления
, силы линейно – вязкого сопротивления  .
. , (1.48)
, (1.48)
 , где
, где  - неизвестные постоянные. Подставим выражений для
- неизвестные постоянные. Подставим выражений для  и
и 
 . (1.49)
. (1.49) (1.50)
(1.50) , а
, а  .
.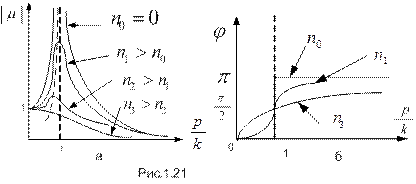
 явно выраженный максимум отсутствует), а частота, при которой наблюдается максимум, смещается в сторону начала координат; сдвиг фаз между перемещением и вынуждающей силой на каждой частоте вынуждающей силы имеет (при заданном сопротивлении) свою величину.
явно выраженный максимум отсутствует), а частота, при которой наблюдается максимум, смещается в сторону начала координат; сдвиг фаз между перемещением и вынуждающей силой на каждой частоте вынуждающей силы имеет (при заданном сопротивлении) свою величину.