 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел функции по КошиСтр 1 из 2Следующая ⇒
Предел функции по Гейне Значение
Предел функции по Коши Значение
Условие (*) можно сформулировать иначе: для любого числа Теорема (критерий Коши).Для того чтобы посл-ть сходилась, необходимо и достаточно, чтобы она удовлетворяла условию Коши. Доказательство. Необходимость. Пусть посл-ть { Зададим Достаточность. Пусть { Пусть Обозначим через 5.Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (илипреде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва). Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю. 1. 6. Бесконечно малые и их свойства. limx® a a(x)=0 Теорема. 1. Если f(x)=b+a, где a - б.м. при x® a, то limx® a f(x)=b и обратно, если limx® af(x)=b, то можно записать f(x)=b+a(x). Теорема. 2. Если limx® a a(x)=0 и a(x) ¹ 0, то 1/a® ¥. Теорема. 3. Сумма конечного числа б.м. есть б.м. Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.
Теорема. 1. Предел суммы есть сумма пределов. Теорема. 2. Предел произведения есть произведение пределов. Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0). Теорема. 4. Если u(x) £ z(x) £ v(x), и limx® a u(x)=limx® a v(x)=b, то limx® a z(x)=b. ("Теорема о двух милиционерах"). Теорема 1. Предел постоянной равен самой постоянной. Доказательство. f(x)=с, докажем, что Возьмем произвольное e>0. В качестве d можно взять любое положительное число. Тогда при Теорема 2. Функция не может иметь двух различных пределов в одной точке. Доказательство. Предположим противное. Пусть По теореме о связи предела и бесконечно малой функции: f(x)-A= f(x)-B= Вычитая эти равенства, получим: B-A= Переходя к пределам в обеих частях равенства при B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему. Теорема 3. Если каждое слагаемое алгебраической суммы функций имеет предел при Доказательство. Пусть Тогда, по теореме о связи предела и б.м. функции: Сложим алгебраически эти равенства: f(x)+g(x)-h(x)-(А+В-С)= где По теореме о связи предела и б.м. функции: Теорема 4. Если каждый из сомножителей произведения конечного числа функций имеет предел при Следствие. Постоянный множитель можно выносить за знак предела. Теорема 5. Если функции f(x) и g(x) имеют предел при причем
§ 7,Первый замечательный предел:
§ Второй замечательный предел:
8.Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C.
Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности: Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями. Теоре́ма Вейерштра́сса в математическом анализе и общей топологии гласит, что функция, непрерывная на компакте, ограничена на нём и достигает своей верхней и нижней грани. Пусть дана непрерывная числовая функция, определённая на отрезке, то есть
— точные верхняя и нижняя грани множества значений функции f соответственно. Тогда эти значения конечны (
Поиск по сайту: |
 называется пределом (предельным значением) функции
называется пределом (предельным значением) функции 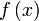 в точке
в точке  , если для любой посл-ти точек
, если для любой посл-ти точек  , сходящейся к
, сходящейся к  сходится к
сходится к 
 такое, что для всех аргументов
такое, что для всех аргументов  , удовл условию
, удовл условию  , выполняется неравенство
, выполняется неравенство  .[1]
.[1]
 } удовлетворяет условию
} удовлетворяет условию  Коши, если для любого числа
Коши, если для любого числа  >0 существует такой номер N, зависящий от
>0 существует такой номер N, зависящий от  <
<  (*).
Посл-ть, удовл условию Коши, называется фундаментальной.
(*).
Посл-ть, удовл условию Коши, называется фундаментальной.
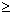 N и всех натуральных p выполняется условие:
N и всех натуральных p выполняется условие:  .
. } сходится и
} сходится и  .
. . Пусть n
. Пусть n  , то есть выполняется условие Коши.
, то есть выполняется условие Коши. . Пусть
. Пусть  такой, что при n
такой, что при n  и m
и m  . В частности, если n
. В частности, если n  , то есть
, то есть 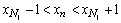 при n
при n  }, n=N
}, n=N 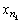 }.
}. . Зададим
. Зададим  ,что для всех номеров K
,что для всех номеров K  n
n 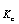 выполняется неравенство
выполняется неравенство 
 =max{N,n
=max{N,n  } и зафиксируем некоторое n
} и зафиксируем некоторое n 
 , что и означает, что
, что и означает, что  (для суперлюбознательных)
(для суперлюбознательных) .
. .
.
 .
. и
и  .
. - б.м. при
- б.м. при  ,
, - б.м. при
- б.м. при 



 .
. ,
, 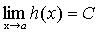 .
.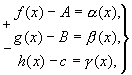 где
где 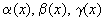 - б.м. при
- б.м. при  ,
, б.м. при
б.м. при  А+В-С=
А+В-С= 


 .
.

 .
. , то и их частное имеет предел при
, то и их частное имеет предел при  ,
, 

 Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C.
Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C. и
и  . Пусть
. Пусть
 ) и достигаются (существуют
) и достигаются (существуют  такие, что
такие, что  ).
).