 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Свойства предельных значений
Предел функции Основное определение.Число b называется предельным значением (пределом)функции f(x) при x стремящимся к a (обозначение
Варианты определения. Число b называется предельным значением (пределом)функции f(x) при x стремящимся к +¥ (обозначение
Говорят, что функция f(x) стремится к +¥ при x стремящимся к a (обозначение
И так далее.
4.1 Предел функции в точке 1. Функция одной переменной. Определение предела функции в точке по Коши.Число bназывается пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любого положительного числа e существует такое положительное число d, что при всех х ≠ а, таких, что |x – a | < d, выполняется неравенство Определение предела функции в точке по Гейне. Число b называется пределом функции у = f(x) при х, стремящемся к а (или в точке а), если для любой последовательности {xn}, сходящейся ка (стремящейся к а, имеющей пределом число а), причем ни при каком значении n хn ≠ а, последовательность {yn = f(xn)} сходится к b. Данные определения предполагают, что функция у = f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Определения предела функции в точке по Коши и по Гейне эквивалентны: если число b служит пределом по одному из них, то это верно и по второму. Указанный предел обозначается так:
Геометрически существование предела функции в точке по Коши означает, что для любого числа e > 0 можно указать на координатной плоскости такой прямоугольник с основанием 2d > 0, высотой 2e и центром в точке (а; b), что все точки графика данной функции на интервале (а–d; а + d), за исключением, быть может, точки М(а; f(а)), лежат в этом прямоугольнике – см. рис.:
Критерий Коши существования предела функции в точке. Число b – предел функции у = f(x) при х, стремящемся к а, тогда и только тогда, когда для любого числа e > 0 можно указать такую проколотую d-окрестность точки а, что для любых чисел х1 и х2, содержащихся в этой окрестности, выполняется неравенство Пусть
В теории пределов доказываются следующие два утверждения. Первый замечательный предел: Второй замечательный предел: При вычислении пределов для раскрытия неопределённостей, связанных с дифференцируемыми функциями, часто используют правило Лопиталя. 4.2 Односторонние пределы.Число b есть предел слева (справа)функции f(x) при x стремящимся к a, если
( Обозначение Если
Теорема,устанавливающая связь понятий предела функции и предела последовательности. Для того, чтобы существовал Свойства предельных значений. Предельные значения имеют такие же свойства, что и предел последовательности:
4.2 Односторонний предел Определения Пусть на некотором числовом множестве
Поиск по сайту: |
 или
или  ), если
), если .
. ), если
), если .
. ), если
), если .
.


 Тогда существуют пределы суммы и произведения функций f(x) и g(x), а в случае с ≠ 0 – и частного этих функций, причём:
Тогда существуют пределы суммы и произведения функций f(x) и g(x), а в случае с ≠ 0 – и частного этих функций, причём:


 то существует и предел сложной функции, причём
то существует и предел сложной функции, причём

 где е – знаменитое иррациональное число, e= 2,71...
где е – знаменитое иррациональное число, e= 2,71...
 ).
). (
(  ).
). ,то существует
,то существует 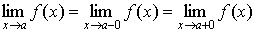 . Верно и обратное утверждение.
. Верно и обратное утверждение. необходимо и достаточно, чтобы для любойпоследовательности {xn}, у которой
необходимо и достаточно, чтобы для любойпоследовательности {xn}, у которой  существовал
существовал 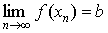
 ,
,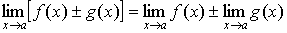 ,
, ,
, , если
, если  .
. задана числовая функция
задана числовая функция  и число
и число  — предельная точка области определения
— предельная точка области определения  . Существуют различные определения для односторонних пределов функции
. Существуют различные определения для односторонних пределов функции  в точке
в точке