 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Общие теоретические сведения. Раздел 8. Методы статистической обработки исследовательских данныхСтр 1 из 2Следующая ⇒
Раздел 8. Методы статистической обработки исследовательских данных Задания и вопросы для подготовки к занятию 1. Предположим, что Вы при проведении своего исследования, предложили свою систему заданий и вопросов, отличную от той, которая предлагается в школьных учебниках. Изменится ли результат обучения при этом? Что, по вашему мнению, может измениться в результатах обучения? А можно ли это изменение «научно» обосновать или «измерить» каким-либо образом? 2. Получив результаты одинаковых контрольных работ в двух классах можно ли по количеству пятёрок утверждать, что где больше пятёрок, там учащиеся усвоили материал лучше? А по количеству пятёрок и четвёрок? Что, на Ваш взгляд, необходимо ещё учитывать, при сравнении результатов? Общие теоретические сведения Для педагога очень важно уметь анализировать результаты своей профессиональной деятельности, а также грамотно планировать и проводить психолого-педагогические эксперименты, обрабатывать их результаты. Специфика статистической обработки результатов психолого-педагогических исследований заключается в том, что анализируемая база данных характеризуется большим количеством показателей различных типов, необходимостью учета объективных и субъективных факторов, сложностью корреляционных связей между переменными выборками. Психолого-педагогические исследования можно разбить на три группы. Первая – номинальные переменные (пол, возраст и другие анкетные данные). Арифметические операции над такими величинами не имеют смысла, поэтому результаты описательной статистики (выборочные средние, дисперсия) к таким величинам не применяются. Классический способ их анализа – разбиение на классы относительно выбранных номинальных признаков и проверка значимости различий по классам. Вторая группа имеет количественную шкалу измерения,которая является порядковой (ординальной). При анализе ординальных переменных используются как разбиение на подвыборки, так и ранговые технологии (например, нахождение ранговой корреляции). Третья группа – количественные переменные, отражающие степень выраженности замеряемого показателя (например, успеваемость; тесты Амтхауэра, Кеттела и другие оценочные тесты). Педагогический (или формирующий) эксперимент – это специфический исключительно для педагогики вид эксперимента, в котором активное воздействие экспериментальной ситуации на испытуемого должно способствовать его развитию и личностному росту. Как правило в эксперименте участвуют две группы: экспериментальная и контрольная. Необходимо, чтобы до эксперимента обе группы несущественно отличались по исследуемому признаку. Только ученикам экспериментальной группы предлагается новый метод обучения (воспитания) или определенное задание, которое (по мнению экспериментаторов) будет способствовать формированию заданного качества. В конце эксперимента две группы снова сравниваются между собой для оценки полученных результатов. Важно не только зафиксировать и сравнить полученные результаты, но и обосновать их, доказать неслучайность и значимость полученных различий. Как правило, установить связь между воздействием на испытуемого и полученным результатом, обосновать эффективность (или неэффективность) проведенного экспериментапедп помогают инструменты математической статистики. Большинство педагогических исследований призвано ответить на вопрос: «Верно ли сделанное предположение?», «Подтверждается ли выдвинутая гипотеза?». Для корректного ислледования необходимо, чтобы выборка в максимальной мере соответствовала генеральной совокупности, отражала наблюдаемые в ней явления, их изменчивость, т.е. была репрезентативной. Наиболее простой способ добиться реперезентативности – это составить выборку методом случайного отбора исследуемых объектов. Данный метод предполагает соблюдение таких условий, при которых каждый член генеральнойс совокупности имеет равные шансы попать в выборку. Наличие кокой-либо закономерности отбора не допускается. Одной из задач педагогического исследования является сравнение полученных результатов. В литературе описаны разнообразные критерии оценки полученных результатов и выдвинутых гипотез. Рассмотрим некоторые из них. Результаты исследования реперезентативной выборки можно подвергать анализу с использованием математичесих методов. Наиболее часто результаты опыта представляют в виде вариационного ряда. Пример 1. Петя и Вася прыгали в длину с места и свои результаты (в см) записали в таблицу.
Кто из ребят прыгает дальше? Кто прыгает стабильнее? Для того, чтобы определить, как сильно отличаются результаты друг от друга, рассматривают показатели рассеивания. Главная характеристика рассеивания вариационного ряда – дисперсия. Чем большее значение дисперсии, тем сильнее отличие значений измеряемой величины друг от друга. По таблице видно, что дальше прыгнул Вася, но результаты стабильнее у Пети (размах и дисперсия его результатов меньше). Пример 2. После написания одной и той же срезовой контрольной работы по математике ученики двух десятых классов одной школы показали следующие результаты при условии, что работы проверял один учитель:
Ученики какого класса справились с контрольной работой лучше? Таким образом, возникает необходимость сравнения данных из нескольких вариационных рядов. Найдем выборочные средние (формула 7.7) для двух классов. Для 10 «А» класса: Для 10 «Б» класса: Заметим, что выборочная средняя в данном примере показывает среднюю оценку десятиклассников. По полученным расчетам можно сделать вывод, что 10 «А» класс с контрольной работой справился лучше, так как в этом классе средняя оценка за контрольную работу выше, чемв 10 «Б». Средний балл для обоих классов равен:
То есть средний балл за контрольную работу в обоих классах выше, чем в «Б», но ниже, чем в «А». Дисперсия позволяет оценить не только степень различия показателей внутри группы, но и может быть использована для определения отклонения данных между разными группами. Для этого используют несколько видов дисперсии: внутригрупповую и межгрупповую. Если в качестве выборки берется какая-либо группа, то дисперсия называется групповой дисперсией. Чтобы отразить различия между дисперсиями нескольких групп, существует понятие межгрупповой дисперсии:
и внутригрупповой дисперсии:
где k – число групп в общей выборке, Во втором примере выборка учащихся разбивается на две группы. Выборочная средняя для всех групп равна:
Так как межгрупповая дисперсия близка к нулю, то можно сделать вывод, что отметки одной группы (10 «А» класса) в малой степени отличаются от отметок второй группы (10 «Б). Иными словами, с тчки зрения межгрупповой дисперсии рассмотренные группы в незначительной степени отличаются по заданному признаку. Межгрупповая и общая дисперсии помогают определить, насколько сильно результат педагогического эксперимента (или друго опыта) обусловлен принадлежностью испытуемого к той или иной группе. Для этого используется коэффициент детерминации Пример 3. Оценки, полученные на ЕГЭ по математике выпускниками классов нс разными профилями, описаны в следующей таблице:
Необходимо определить, в какой степени успешность сдачи ЕГЭ зависит от принадлежности у к тому или инму потоку. Решение. Найдем средний балл за экзамен для всей совокупности испытуемых:
Найдем межгрупповую дисперсию:
Найдем внутригрупповую дисперсию:
Определим общую дисперсию: Dв=Dвнгр+Dмежгр=9,98+45,66=55,64, тогда Полученный коэффициент детерминации показывает, что успешность сдачи ЕГЭ в данном опыте не 82% обусловлена принадлежностью учащегося к той или иной группе. Используется также эмпирическое корреляционное отношение, получаемое извлечением квадратного корня из коэффициента детерминации. В рассматриваемом примере Чем ближе значение корреляционного отношения к единице, тем более тесная связь существует в рассматриваемом опыте. В данном случае показано наличие тесной связи между успешностью сдачи ЕГЭ и принадлежностью учащегося к той или иной группе обучаемых. Общая дисперсия помогает численно оценить, как сильно отличаются варианты выборки друг от друга. Межгрупповая дисперсия помогает выявить степень различия между группами данной выборки. Однако в педагогических исследованиях зачастую не требуется численная оценка параметра, но при этом важно знать существенно ли отличаются испытуемые (или группа испытуемых) друг от друга по тому или иному признаку. Ответ на такой вопрос дает коэффициент вариации. На разных этапах статистического исследования возникает необходимость в формировании и экспериментальной проверке некоторых предполагаемых утверждений (гипотез). Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения не известен, но имеются основания предположить, что он имеет вид А, выдвигают гипотезу: генеральная совокупность распределена по закону А. Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет опровергнута, то имеет место противоречащая ей гипотеза. Нулевой (основной) называют выдвинутую гипотезу Но. Конкурирующей (альтернативной) называют гипотезу Н1, которая противоречит нулевой. Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 5, то конкурирующая гипотеза, в частности, может состоять в предположении, что а≠5. Коротко записывают так: Но: а=5; Н1: а≠5. Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку проводят статистическими методами, то ее называют статистической. В итоге проверки гипотезы в двух случаях может быть принято неправильное решение, т. е. могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность совершить ошибку первого рода принято обозначать α; ее называют уровнем значимости. Например, если принят уровень значимости, равный 0,03, то это означает, что в трех случаях из ста имеется риск допустить ошибку первого рода (опровергнуть правильную гипотезу). Для проверки нулевой гипотезы используют специально подобранную величину, точное или приближенное значение которой известно. Эту величину обозначают через U или Z, если она распределена нормально; υ2 или F – по закону Фишера или Т – по закону Стьюдента, χ2 – по закону «хи квадрат» и т.д. Статистическим критерием (или просто критерием) называют случайную величину, которая служит для проверки нулевой гипотезы. Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия принимают отношение исправленных выборочных дисперсий:
Эта величина случайная, потому что в различных опытах дисперсии принимают различные, наперед неизвестные значения. Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия. Наблюдаемым значением называют значение критерия, вычисленное по выборкам. Например, если по двум выборкам найдены исправленные выборочные дисперсии
После выбора определенного критерия множество всех его значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – при которых она принимается. Критическая область – совокупность значений критерия, при которых гипотезу отвергают. Область принятия гипотезы –совокупность значений критерия, при которых гипотезу принимают. Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу отвергают. Критическими точками (границами) называют точки, отделяющие критическую область от области принятия гипотезы. Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критическую области. Рассмотрим один из методов проверки гипотезы – сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны. Пусть генеральные совокупности X и Y распределены нормально, их дисперсии известны (или найдены). По независимым выборкам, объемы которых п и т, извлеченным из этих совокупностей, найдены средние Учитывая, что Такая задача ставится потому, что выборочные средние, как правило, оказываются различными. Возникает вопрос: значимо или незначимо различаются выборочные средние? Правило. Для того, чтобы при заданном уровне значимости проверить α проверить нулевую гипотезу Но: М(Х) =М(Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе: 1) Н1: М(Х) ≠ М(Y) (критическая область – двусторонняя) надо вычислить наблюдаемое значение критерия
по таблице функции Лапласа (приложение) найти критическую точку из равенства
Если Если 2) Н1: М(Х) > М(Y) (критическая область – правосторонняя) надо вычислить наблюдаемое значение критерия по формуле (8.2), по таблице функции Лапласа найти критическую точку из равенства
Если Если 3) Н1: М(Х)< М(Y) (критическая область – левосторонняя) надо вычислить наблюдаемое значение критерия по формуле (8.2), по таблице функции Лапласа найти критическую точку из равенства
Если Если Пример 4. По двум неизвестным выборкам, объемы которых соответственно равны п=60 и т=50, извлеченным из нормальных генеральных совокупностей, найдены выборочные средние Решение. Найдем наблюдаемое значение критерия:
По условию конкурирующая гипотеза имеет вид М (Х) ≠ М(Y), поэтому критическая область – двусторонняя. Найдем правую критическую точку:
Поиск по сайту: |
 .
. .
. .
. , (8.1)
, (8.1) (8.2)
(8.2) – выборочная средняя для всех групп;
– выборочная средняя для всех групп;  – выборочная средняя, Di. – дисперсия и
– выборочная средняя, Di. – дисперсия и  – объем выборки i-й группы.
– объем выборки i-й группы. (ранее она была найдена другим способом).
(ранее она была найдена другим способом).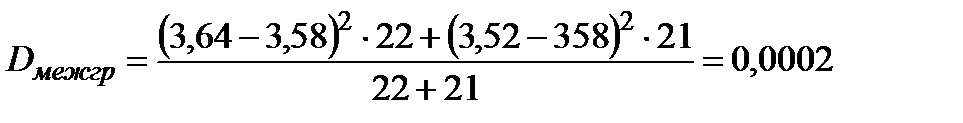 .
. . (8.3)
. (8.3)




 . (8.4)
. (8.4) и
и  , то наблюдаемое значение критерия F
, то наблюдаемое значение критерия F  .
. и
и  . Требуется по выборочным средним при заданном уровне значимости α проверить нулевую гипотезу, состоящую в том, что генеральные средние (математические ожидания) рассматриваемых совокупностей равны между собой, т.е. Но: М(Х) =М(Y).
. Требуется по выборочным средним при заданном уровне значимости α проверить нулевую гипотезу, состоящую в том, что генеральные средние (математические ожидания) рассматриваемых совокупностей равны между собой, т.е. Но: М(Х) =М(Y). и
и  , нулевую гипотезу можно записать так: Но:
, нулевую гипотезу можно записать так: Но:  .
. , (8.5)
, (8.5) . (8.6)
. (8.6) – нет оснований отвергать нулевую гипотезу.
– нет оснований отвергать нулевую гипотезу.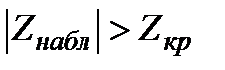 – нулевую гипотезу отвергают.
– нулевую гипотезу отвергают. . (8.7)
. (8.7) – нет оснований отвергать нулевую гипотезу.
– нет оснований отвергать нулевую гипотезу. – нулевую гипотезу отвергают.
– нулевую гипотезу отвергают. – нет оснований отвергать нулевую гипотезу.
– нет оснований отвергать нулевую гипотезу. – нулевую гипотезу отвергают.
– нулевую гипотезу отвергают. .
.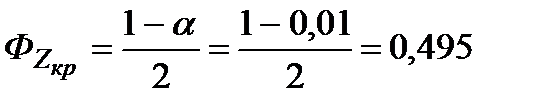 . По таблице Лапласа находим Zкр =2,58. Так как
. По таблице Лапласа находим Zкр =2,58. Так как