 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теоремы о сходящихся последовательностяхСтр 1 из 3Следующая ⇒
Монотонность и ограниченность последовательности Последовательность Возрастающие, убывающие, невозрастающие и неубывающие последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными. Последовательность Пример. Доказать, что последовательность Решение. Рассмотрим разность
Полученное выражение больше нуля для любого натурального n. Следовательно, Задачи. Написать первые пять членов последовательности: 6.1. 6.3. Написать формулу n-ого члена последовательности: 6.5. 6.6. 6.7. 6.8. 6.9. Какие из последовательностей являются монотонными, строго монотонными, ограниченными: 6.10. 6.12. 6.14. 6.16.
Предел последовательности Число а называется пределом последовательности На e-языке это определение можно записать следующим образом:
Последовательность, имеющая предел, называется сходящейся. Последовательность, у которой нет предела, называется расходящейся. Интервал Теоремы о сходящихся последовательностях 1. Сходящаяся последовательность 2. Сходящаяся последовательность ограничена. 3. Предел постоянной равен этой постоянной, т.е. 4. Пусть существуют пределы последовательностей а) существуют пределы последовательностей
б) существует предел последовательности
в) если bn ¹ 0 при всех последовательности
Поиск по сайту: |
 называется возрастающей (соответственно убывающей), если для любого номера n выполняется неравенство
называется возрастающей (соответственно убывающей), если для любого номера n выполняется неравенство  (соответственно
(соответственно  ); неубывающей (соответственно невозрастающей), если для любого номера n выполняется неравенство
); неубывающей (соответственно невозрастающей), если для любого номера n выполняется неравенство  (соответственно
(соответственно 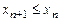 ).
). (соответственно
(соответственно  ). Последовательность
). Последовательность 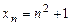 является монотонной.
является монотонной. .
. ; 6.2.
; 6.2.  ;
; ; 6.4.
; 6.4.  .
.




 ; 6.11.
; 6.11. 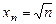 ;
; ; 6.13.
; 6.13.  ;
; ; 6.15.
; 6.15.  ;
; ; 6.17.
; 6.17.  .
. , если для любого, сколь угодно малого
, если для любого, сколь угодно малого  , существует номер
, существует номер  такой, что при
такой, что при  выполняется неравенство
выполняется неравенство 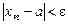 .
. .
. называется e-окрестностью точки а. Определение предела имеет следующий геометрический смысл: число а является пределом последовательности
называется e-окрестностью точки а. Определение предела имеет следующий геометрический смысл: число а является пределом последовательности  .
. (
(  и
и  ). Тогда:
). Тогда: , причем
, причем ;
;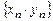 , причем
, причем ;
; , существует предел
, существует предел , причем
, причем .
.