 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Указания к лабораторной работе №5Стр 1 из 2Следующая ⇒
Лабораторная работа №5 – Статистическое изучение динамики социально – экономических явлений и процессов Указания к лабораторной работе №5 Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для ее отражения строятся ряды динамики. Существуют различные виды рядов динамики: интервальные и моментные; с равноотстоящими уровнями во времени и неравноотстоящими уровнями. Важнейшим условием правильного построения ряда динамики является сопоставимость всех входящих в него уровней. Динамические ряды анализируются при помощи ряда показателей, определяющих направление, характер и интенсивность количественных изменений явлений во времени. К таким показателям относятся: - абсолютный прирост (цепной):
- абсолютный прирост (базисный):
где
- темп роста (цепной):
- темп роста (базисный):
- темп прироста:
- абсолютное значение одного процента прироста:
Для получения обобщающих показателей динамики социально-экономических явлений рассчитывают средние величины: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста. Методы расчета среднего уровня ряда динамики зависят от вида ряда динамики. Для расчета среднего уровня интервального ряда динамики: - с равноотстоящими уровнями во времени применяют среднюю арифметическую простую:
где
- с неравноотстоящими уровнями во времени используют среднюю арифметическую взвешенную:
где
Средний уровень моментного ряда динамики: - с равностоящими уровнями определяют по формуле средней хронологической:
- с неравностоящими уровнями рассчитывают по формуле средней хронологической взвешенной:
Средний абсолютный прирост: - цепной:
где
- базисный:
где
Средний темп роста: - цепной:
где
- базисный:
где
Средний темп прироста:
Одна из важнейших задач анализа ряда динамики заключается в установлении закономерностей развития явления или процесса. В этих целях определяется основная тенденция развития (тренд). Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом основная тенденция развития
Определение теоретических (расчетных) уровней
Для выравнивания ряда динамики по прямой используется уравнение:
где а – свободный член уравнения, равный среднему уровню тренда для периода (момента) с нулевым номером b – главный параметр линейного тренда – среднее абсолютное изменение за принятую в ряду единицу времени.
Величина параметров а и b определяется по методу наименьших квадратов (МНК) путем приравнивания частных первых производных функции
Для упрощения расчетов параметры уравнения могут быть определены с помощью способа отсчета от условного нуля, суть которого заключается в том, что показателям времени
Для отображения основной тенденции развития явления во времени также применяется уравнение параболы II порядка:
где а – средний (выравненный) уровень тренда для периода (момента) с нулевым номером b – средний за весь период среднегодовой прирост, который уже не является константой, а изменяется равномерно со средним ускорением, равным 2с; с – главный параметр параболы – константа.
Для вычисления параметров а, b и с по методу наименьших квадратов три частные производные функции
При переносе начала отсчета периодов (моментов) времени в середину ряда суммы нечетных степеней номеров этих периодов
Первое и третье уравнения последней системы образуют систему из двух уравнений с двумя неизвестными:
Проверка адекватности построенной модели тренда реальному процессу в самом простом случае строится на анализе коэффициент детерминации
где n – количество уровней ряда; k – число определяемых параметров модели;
Коэффициент детерминации
Выполнение заданий №1 и №3 лабораторной работы №5 не предполагает использование специальных функций ППП Microsoft Excel, однако в целях упрощения расчетов возможно задание формул в ячейках электронных таблиц данной программы. Для решения задания №2 следует обратиться к [13, стр. 322-329 и др.].
Поиск по сайту: |
 ;
; ,
,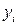 - уровень сравниваемого периода;
- уровень сравниваемого периода; - уровень предшествующего периода;
- уровень предшествующего периода; - уровень базисного периода;
- уровень базисного периода; ;
; ;
; ;
; .
. ,
, - абсолютные уровни ряда;
- абсолютные уровни ряда; - число уровней ряда.
- число уровней ряда. ,
, - длительность интервала времени между уровнями.
- длительность интервала времени между уровнями. ;
; .
. ,
,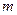 - число цепных абсолютных приростов (
- число цепных абсолютных приростов (  ) в изучаемом периоде.
) в изучаемом периоде. ,
, ,
, ,…,
,…,  – цепные коэффициенты роста.
– цепные коэффициенты роста. ,
, .
.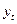 рассчитывается как функция времени:
рассчитывается как функция времени: .
. производится на основе адекватной математической функции, которая наилучшим образом отображает основную тенденцию ряда динамики. Подбор адекватной функции осуществляется методом наименьших квадратов – минимальностью отклонений суммы квадратов между теоретическими уровнями и наблюдаемыми:
производится на основе адекватной математической функции, которая наилучшим образом отображает основную тенденцию ряда динамики. Подбор адекватной функции осуществляется методом наименьших квадратов – минимальностью отклонений суммы квадратов между теоретическими уровнями и наблюдаемыми: .
. ,
, - уровень тренда для периода или момента с номером
- уровень тренда для периода или момента с номером 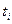 ;
; к нулю. Тогда система нормальных уравнений имеет вид:
к нулю. Тогда система нормальных уравнений имеет вид: .
. придают такие значения, чтобы их сумма была равна нулю, т.е.
придают такие значения, чтобы их сумма была равна нулю, т.е.  . В этом случае параметры уравнения линейного тренда рассчитываются по формулам:
. В этом случае параметры уравнения линейного тренда рассчитываются по формулам: ;
; .
. ,
, приравниваются к нулю, и после преобразований можно получить систему трех уравнений с тремя неизвестными:
приравниваются к нулю, и после преобразований можно получить систему трех уравнений с тремя неизвестными: .
. и
и  обращаются в ноль. При этом второе уравнение обращается в уравнение с одним неизвестным, откуда:
обращаются в ноль. При этом второе уравнение обращается в уравнение с одним неизвестным, откуда: .
. .
. :
: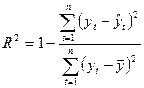 ,
, - оценка уровней ряда по модели;
- оценка уровней ряда по модели; - среднее арифметическое значение уровней ряда.
- среднее арифметическое значение уровней ряда. , объясняемую уравнением тренда, в его общей дисперсии. Чем ближе величина коэффициента детерминации к 1 (или 100%), тем лучше качество построенной модели тренда.
, объясняемую уравнением тренда, в его общей дисперсии. Чем ближе величина коэффициента детерминации к 1 (или 100%), тем лучше качество построенной модели тренда.