 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лінійні неоднорідні диференціальні рівняння (ЛНДР) ІІ-го порядку. Теорема про структуру розв’язку ⇐ ПредыдущаяСтр 5 из 5
Лінійне неоднорідне д. р. ІІ-го порядку має вигляд
де f(x) – відома неперервна на деякому інтервалі функція (вільний член). Розглянемо окремий випадок, коли p і q – сталі. Нехай відповідне однорідне рівняння
має загальний розв’язок Теорема(про структуру загального розв’язку ЛНДР). Загальний розв’язок лінійного неоднорідного д. р. (1) (
Далі зупинимось на двох випадках розв’язання ЛНДР, коли вільний член 1) 2) 12. Розв’язання ЛНДР ІІ-го порядку із сталими коефіцієнтами і вільним членом Нехай задано ЛНДР
де
Нам вже відомо, що загальний розв’язок однорідного д. р. записується однією з формул якщо
якщо
якщо Відповідно вільному члену
де
Запишемо ще декілька виразів для
Розглянемо тепер кілька прикладів на складання Приклади. Записати
Розв’язання. 1. Знаходимо корені характеристичного рівняння
3.
4.
5.
6.
Приклад. Знайти загальний розв’язок д. р.
Розв’язання. Виконаємо за таким алгоритмом. 1. Знаходимо загальний розв’язок однорідного д. р.
Відповідно формулі (2) маємо
2. Складаємо (8) маємо
3. Знаходимо
4. Підставимо
Прирівнюємо коефіцієнти при однакових степенях
Отже,
шуканий загальний розв’язок. Розв’язати самостійно
13. Розв’язання ЛНДР ІІ-го порядку із сталими коефіцієнтами і вільним членом Розглянемо ЛНДР
- відповідне однорідне рівняння,
- його характеристичне рівняння з коренями у вигляді
де А і В – невідомі коефіцієнти, число Приклад. Знайти загальний розв’язок д. р.
Розв’язання. 1. Знаходимо загальний розв’язок д. р.
2. З правої частини (4) знаходимо
3. Знаходимо
4. Підставимо
Прирівняємо коефіцієнти при
Тоді маємо
а загальний розв’язок запишеться
Розв’язати самостійно
Поиск по сайту: |
 , (1)
, (1) (2)
(2) , який знаходиться за однією з формул (3) - (5) попереднього параграфа. Нехай, далі,
, який знаходиться за однією з формул (3) - (5) попереднього параграфа. Нехай, далі,  - деякий частинний розв’язок ЛНДР (1). В подальшому будемо опиратись на таку теорему (подаємо без доведення).
- деякий частинний розв’язок ЛНДР (1). В подальшому будемо опиратись на таку теорему (подаємо без доведення). ) дорівнює сумі загального розв’язку (
) дорівнює сумі загального розв’язку (  , (3)
, (3)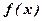 має спеціальний вигляд:
має спеціальний вигляд: , де
, де 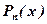 - заданий многочлен,
- заданий многочлен,  - відоме число;
- відоме число; , де
, де  - задані.
- задані. .
. , (1)
, (1) - відомі числа,
- відомі числа, 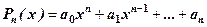 - многочлен порядку (степеня)
- многочлен порядку (степеня)  , коефіцієнти, якого теж відомі. Загальний розв’язок ЛНДР (1) будемо знаходити у відповідності з теоремою про структуру:
, коефіцієнти, якого теж відомі. Загальний розв’язок ЛНДР (1) будемо знаходити у відповідності з теоремою про структуру: , (2)
, (2)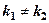 - дійсні;
- дійсні; , (3)
, (3) - дійсні і рівні;
- дійсні і рівні; (4)
(4) - комплексні.
- комплексні.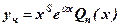 , (5)
, (5)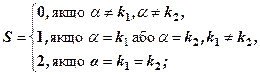 (6)
(6) - многочлен степеня
- многочлен степеня  в залежності від порядка n. Так якщо
в залежності від порядка n. Так якщо
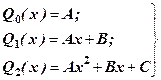 (7)
(7)

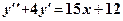



 .
.  . З правої частини
. З правої частини  знаходимо степінь многочлена
знаходимо степінь многочлена  , коефіцієнт при
, коефіцієнт при  в показнику степеня
в показнику степеня 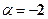 . Поскільки
. Поскільки  і
і  , то за формулою (6)
, то за формулою (6)  .Отже, за формулою(4)
.Отже, за формулою(4)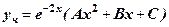 .
. . З правої частини д. р.
. З правої частини д. р.  , тому
, тому  . Поскільки
. Поскільки  , то
, то  і
і  , тому за формулою (6)
, тому за формулою (6)  . Отже,
. Отже, .
. . З правої частини
. З правої частини  маємо
маємо  , тоді
, тоді  ,
,  і
і  , тому
, тому  . Отже,
. Отже, .
. ,
,  і
і  .
. ,
,  . Отже,
. Отже, .
.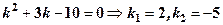 ,
,  .
.  ,
,  , тому
, тому .
.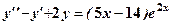 . (8)
. (8) ,
, - дійсні і різні.
- дійсні і різні. .
.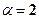 - співпадає з
- співпадає з 
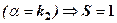 . Отже,
. Отже,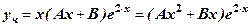 .
. ,
,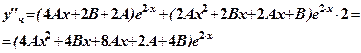
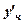 ,
,  в початкове д. р. (8) , при цьому обидві частини скоротимо на
в початкове д. р. (8) , при цьому обидві частини скоротимо на 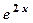 , отримаємо
, отримаємо
 .
.
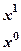
 .
. .
. -
-


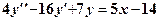



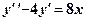






 (1)
(1)
 і
і  . Нехай
. Нехай  (3)
(3) . Якщо ж один з коренів дорівнює
. Якщо ж один з коренів дорівнює  .
. . (4)
. (4) ,
, .
. .
. , число
, число  співпадає з одним з коренів характеристичного рівняння, тому
співпадає з одним з коренів характеристичного рівняння, тому  .
. ,
, .
. .
.
 і
і 

 .
. ,
, .
. .
.
 .
.
 .
.

 .
.
 .
.
 .
.
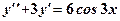 .
.
 .
.
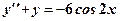 .
.