|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные теоретические сведения. Аппроксимацией называют описание некоторой, порой не заданной явно
Аппроксимацией называют описание некоторой, порой не заданной явно, зависимости или совокупности представляющих ее данных с помощью другой, более простой или более единообразной зависимости. Часто данные находятся в виде отдельных узловых точек, координаты которых задаются таблицей данных. Результат аппроксимации может не проходить через узловые точки. Для обработки данных Matlab использует различные функции интерполяции и аппроксимации данных. Одна из наиболее известных аппроксимаций — полиномиальная. В системе Matlab определены функции аппроксимации данных полиномами по методу наименьших квадратов – полиномиальной регрессии. Это выполняет функция, приведенная ниже: – polyfit(x, y, n) – возвращает вектор коэффициентов полинома р(х) степени n, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию у(х). Результатом является вектор–строка длиной n+1, содержащий коэффициенты полинома в порядке уменьшения степеней х и у равно n+1, то реализуется обычная полиномиальная аппроксимация, при которой график полинома точно проходит через узловые точки с координатами (х. у), хранящиеся в векторах х и у. В противном случае точного совпадения графика с узловыми точками не наблюдается;
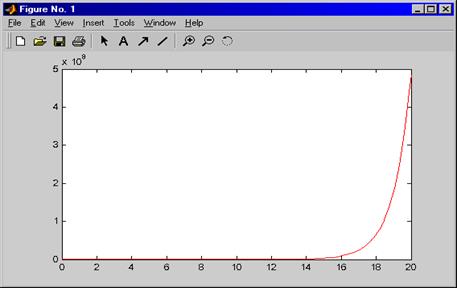
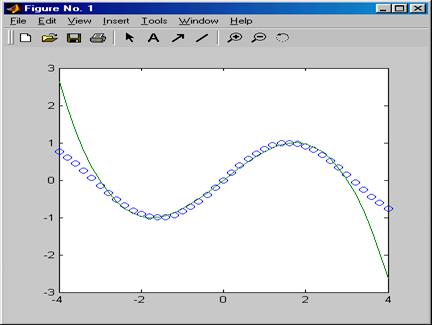
Пример (полиномиальная регрессия для функции s
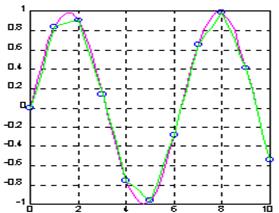
График аппроксимирующего полинома третьей степени на рис. 6.1 показан сплошной линией, а точки исходной зависимости обозначены кружками. К сожалению, при степени полинома свыше 5 погрешность полиномиальной регрессии (и аппроксимации) сильно возрастает и ее применение без центрирования и масштабирования становится рискованным. При полиномиальной регрессии узловые точки не ложатся точно на график полинома, поскольку их приближение к нему является наилучшим в смысле минимального среднеквадратического отклонения.
Интерполяция функций Под интерполяцией обычно подразумевают вычисление значений функции f(x) в промежутках между узловыми точками. Линейная, квадратичная и полиномиальная интерполяция реализуются при полиномиальной аппроксимации. А вот для периодических (и особенно для гладких периодических) функций хорошие результаты может дать их интерполяция тригонометрическим рядом Фурье. Для этого используется следующая функция:
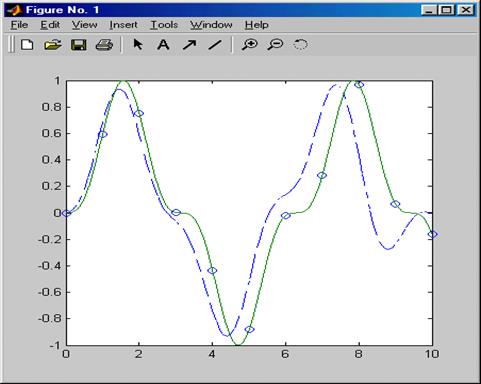
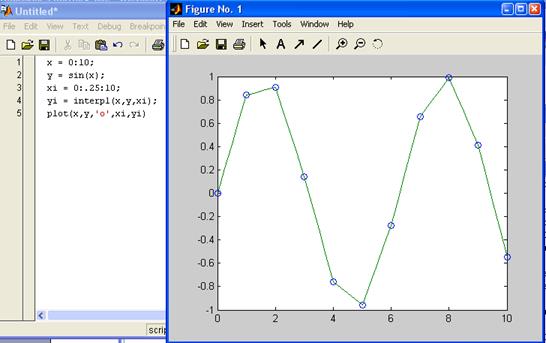
В ряде случаев очень удобна сплайновая интерполяция и аппроксимация таблично заданных функций. При ней промежуточные точки ищутся по отрезкам полиномов третьей степени – это кубическая сплайновая интерполяция. При этом обычно такие полиномы вычисляются так, чтобы не только их значения совпадали с координатами узловых точек, но также, чтобы в узловых точках были непрерывны производные первого и второго порядков. Такое поведение характерно для гибкой линейки, закрепленной в узловых точках, откуда и происходит название spline (сплайн) для этого вида интерполяции (аппроксимации). Для одномерной табличной интерполяции используется функция interpl: –yi = interp1(x, y, xi) — возвращает вектор yi, содержащий элементы, соответствующие элементам xi и полученные интерполяцией векторов х и y. Вектор х определяет точки, в которых задано значение y. –yi = interp1(x, y, xi, method) — позволяет с помощью параметра method задать метод интерполяции: –'nearest' – ступенчатая интерполяция; –'linear' – линейная интерполяция (принята по умолчанию); –'spline' – кубическая сплайн-интерполяция; –'cubic' или 'pchip' – интерполяция многочленами Эрмита. Сплайн – интерполяция используется для представления данных отрезками полиномов невысокой степени – чаще всего третьей. При этом кубическая интерполяция обеспечивает непрерывность первой и второй производных результата интерполяции в узловых точках. Реализуется сплайн-интерполяция следующей функцией: –yi = spline(x, y, xi) – использует векторы х и у, содержащие аргументы функции и ее значения, и вектор xi, задающий новые точки. Пример:Зададим синусоиду всего 10 точками и проведем интерполяцию, используя мелкую сетку.
x = 0:10; y = sin(x);
Решение большинства задач интерполяции и аппроксимации функций и табличных данных обычно сопровождается их визуализацией. Она, как правило, заключается в построении узловых точек функции (или табличных данных) и в построении функции аппроксимации или интерполяции (рис.6.3). В Matlab совмещение функций аппроксимации с графической визуализацией доведено до логического конца – предусмотрена аппроксимация рядом методов точек функции, график которой построен. И все это выполняется прямо в окне редактора графики Property Editor. Для этого в позиции Toolsграфического окна имеются две новые команды:
Рисунок 6.3 – Пример визуализации процесса интерполяции
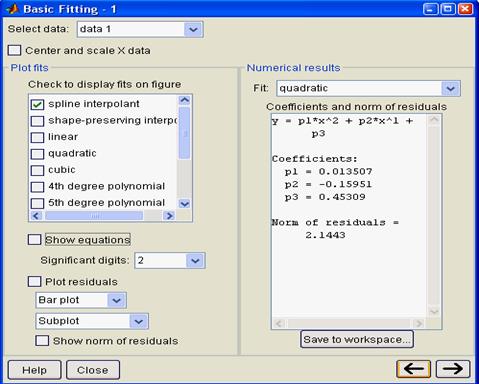
Basic Fitting – основные виды аппроксимации (регрессии); Команда Basic Fitting открывает окно, дающее доступ к ряду видов аппроксимации и регрессии: сплайновой, эрмитовой и полиномиальной со степенями от 1 (линейная аппроксимация) до 10. В том числе со степенью 2 (квадратичная аппроксимация) и 3 (кубическая аппроксимация) (рис.6.4).
Рисунок 6.4 – Окно доступа к видам аппроксимации и регрессии
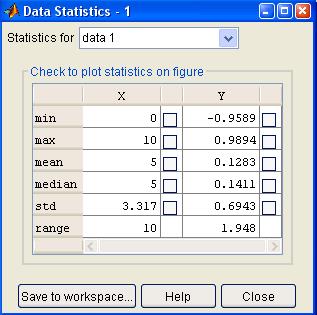
Data Statistics – статистические параметры данных. Команда Data Statistics открывает окно с результатами простейшей статистической обработки данных (рис.6.5).
Рисунок 6.5 – Окно результатов статистической обработки
Анализ поведения многих систем и устройств в динамике базируются на решении систем обыкновенных дифференциальных уравнений (ОДУ). Их, как правило, представляют в виде системы из дифференциальных уравнений первого порядка в форме Коши:
где Параметр t не обязательно означает время, хотя чаще всего решение дифференциальных уравнений ищется во временной области. Вектор b задает начальные и конечные условия. Для решения систем ОДУ в MatLab реализованы различные методы. Их реализации названы решателями ОДУ. Решатели реализуют следующие методы решения систем дифференциальных уравнений, причем для решения жестких систем уравнений рекомендуется использовать, только специальные решатели ode45, ode23: – ode45 – одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка. Это классический метод, рекомендуемый для начальной пробы решения. – ode23 – одношаговые явные методы Рунге-Кутта 2-го и 4-го порядка. Синтаксис: [t, X] = ode23(‘<имя функции>‘, t0, tf, x0)
Описание: Любая система нелинейных ОДУ может быть представлена как система дифференциальных уравнений 1-го порядка в явной форме Коши:
где x - вектор состояния; t - время; f - нелинейная вектор-функция от переменных x, t. Функции: [t, X] = ode23(‘<имя функции>‘, t0, tf, x0, tol, trace) и [t, X] = = ode45(‘<имя функции>‘, t0, tf, x0, tol, trace) интегрируют системы ОДУ, используя формулы Рунге - Кутты соответственно 2-го и 3-го или 4-го и 5-го порядка. Эти функции имеют следующие параметры: Входные параметры: Выходные параметры: Примеры: Рассмотрим дифференциальное уравнение 2-го порядка, известное как уравнение Ван дер Поля,
Это уравнение может быть представлено в виде системы ОДУ в явной форме Коши:
Первый шаг процедуры интегрирования - это создание М-файла для вычисления правых частей ОДУ; присвоим этому файлу имя vdpol.
function xdot = vdpol(t, x)
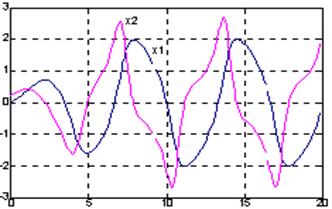
Чтобы проинтегрировать систему ОДУ, определяемых функцией vdpol в интервале времени 0 <= t <= 20, вызовем функцию ode23: t0 = 0; tf = 20;
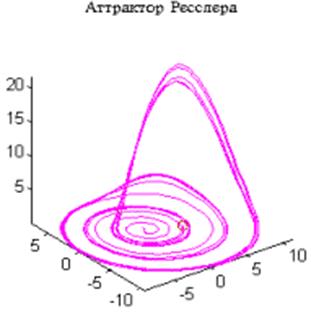
Рассмотрим простейший из известных примеров странного аттрактора - аттрактор Ресслера [7]:
где параметры {a, b, c} имеют значения {0.2 0.2 5.7}, а начальное условие задается следующим образом: x0 = [-0.7 -0.7 1]. Для того чтобы проинтегрировать эту систему в интервале времени 0<= t<= 20, вызовем функцию ode45: t0 = 0; tf = 20;
В описанных далее функциях для решения систем дифференциальных уравнений приняты следующие обозначения и правила: – options — аргумент, создаваемый функцией odeset (еще одна функция позволяет вывести параметры, установленные по умолчанию); – tspan — вектор, определяющий интервал интегрирования [t0 tfinal]. Для получения решений в конкретные моменты времени t0, tl,..., tfinal (расположенные в порядке уменьшения или увеличения) нужно использовать tspan = [t0 tl ... tfinal]; – у0— вектор начальных условий; – pi, р2,.. — произвольные параметры, передаваемые в функцию F; – Т, Y — матрица решений Y, где каждая строка соответствует времени, возвращенном в векторе-столбце Т. Описание функций для решения систем дифференциальных уравнений: – [T, Y] = solver(@F,tspan,у0) — где вместо solver подставляем имя конкретного решателя — интегрирует систему дифференциальных уравнений вида у'=F(t,y) на интервале tspan с начальными условиями у0, @F — дескриптор ODE-функции. Каждая строка в массиве решений Y соответствует значению времени, возвращаемому в векторе-столбце Т; – [T, Y] = solver(@F, tspan, y0, options) — дает решение, подобное описанному выше, но с параметрами, определяемыми значениями аргумента options, созданного функцией odeset. Технология решения дифференциальных уравнений в системе MatLab такова: 1) Создание m–файла. Независимо от вида системы он имеет вид: function dy = solverDE(t, y) dy = zeros(n, 1); dy(1) = f1 (t, y(1), y(2), …, y(n)); dy(2) = f2 (t, y(1), y(2), …, y(n)); …………………………… dy(n) = fn (t, y(1), y(2), …, y(n));
2) Получение решения и сопровождающий его график:
>> [T, Y] = solver(‘solverDE’, [t0 tfinal], [y10 y20 … yn0]); >> plot(T, Y)
Пусть, к примеру, требуется решить дифференциальное уравнение:
с единичными начальными условиями. Данное дифференциальное уравнение второго порядка приведем к системе дифференциальных уравнений первого порядка:
с начальными условиями у1(0) = 1, у2(0) = 1, у3(0) = 1. Вектор
Рисунок 6.6 – Пример создания функции для решения системы ОДУ
Теперь можно вызывать функцию ode45, находящую решение нашей системы дифференциальных уравнений с начальными условиями [1,1,1] на отрезке [0,20] (рис. 6.7)
>> y0=[1 1 1 ]; >> tspan=[0 20]; >> [T,Y]=ode45('ex21',tspan,y0); >> plot(T,Y)
Рисунок 6.7 – Результат работы программы
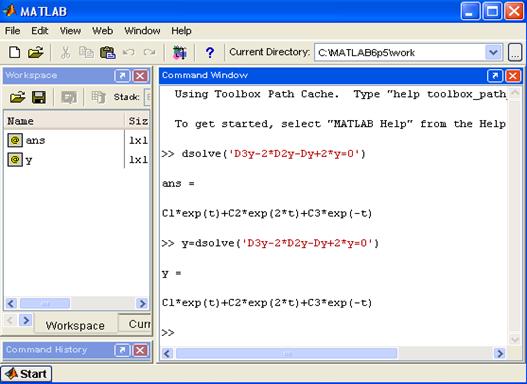
Для решения дифференциальных уравнений в MatLab зарезервирована функция dsolve, которая имеет следующие форматы обращения и возвращает аналитическое решение системы дифференциальных уравнений с начальными условиями: –y=dsolve( 'Dy(x)' ), где Dу(х) – уравнение; у – возвращаемые функцией dsolve решения; –y=dsolve ('Dy(x)', 'НУ'), где Dу(х) – уравнение; НУ – начальные условия. Первая производная функции обозначается Dу, вторая производная – D2у и так далее. Функция dsolve предназначена также для решения системы дифференциальных уравнений. В этом случае она имеет следующий формат обращения: – [f,g] =dsolve('Df(x),Dg(x)', 'НУ'), где Df(x) ,Dg(x) – система уравнений, НУ – начальные условия. Решить дифференциальное уравнение (2) с использованием функции dsolve(рис. 6.8).
Рисунок 6.8 – Пример использования команды dsolve
Поиск по сайту: |
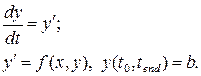 (1)
(1)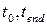 – начальные и конечные точки интервалов.
– начальные и конечные точки интервалов.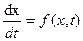 ,
,
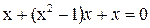
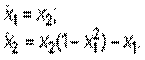
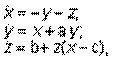
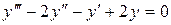 (2)
(2)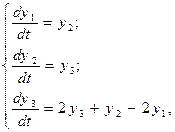 (3)
(3)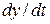 правых частей системы уравнений вычисляем с помощью собственной функции ex21 (рис. 6.6):
правых частей системы уравнений вычисляем с помощью собственной функции ex21 (рис. 6.6):