 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение символьной переменной
Введем команду » sin(x).^2+cos(x).^2 ??? Undefined function or variable 'x'. Величина х воспринимается как числовая переменная, поэтому появляется сообщение: «Функция или переменная ‘x’ не определены». Для того чтобы операция была корректной, величину х необходимо определить как символьную, например » x=sym(‘x’); Альтернативный вариант определения символьной переменной (применяется также применительно к групповым определениям): » syms x; Продолжаем пример: » sin(x)^2+cos(x)^2 ans = sin(x)^2+cos(x)^2 Переменная ans в данном случае имеет смысл символьного выражения. Проверяем, нельзя ли его упростить, т.е. привести к более компактной форме: » simplify(ans) ans = Следует обратить внимание на то, что результат выполнения символьной операции выводится без отступа. Более простой способ решения данной задачи: » sin('x')^2+cos('x')^2 ans = Основные функции Функция expand(s)представляет элементы символьного выражения в развернутой форме: » expand((x-2)^3*(1-x)) ans = 7*x^3-x^4-18*x^2+20*x-8 Функция factor(s)используется для разложения символьного выражения на простые множители: » factor(sym('125')) ans = (5)^3 или символьные: » syms a b; A=[a^2-b^2,a^3+b^3]; » factor(A) ans = [(a-b)*(a+b), (a+b)*(a^2-a*b+b^2)] Данная функция применяется также при разложении скалярных чисел на простые множители: » factor(sym('5040')) ans = (2)^4*(3)^2*(5)*(7) В этом примере 5040=7!; встроенной функции, вычисляющей факториал n!, нет, но ее нетрудно создать самостоятельно (и включить в соответствующий раздел системы): % Вычисление факториала n! function ypr=fact(n); ypr=1; if n~=0 for k=1:n ypr=ypr*k; End End Функция subs– подстановка: subs(s) – замена свободных символьных переменных их числовыми значениями из рабочего пространства: » a=1; » u=sym('sin(pi/(2*a))'); » subs(u) % sin(pi/2) ans = subs(s,new)– замена свободных символьных переменных их числовыми значениями из списка new: » syms a s x » x=pi/16; » u=sin(a^s*x); » subs(u,[a s],[2 3]) % sin(pi/2) ans = subs(s,old,new)– замена свободных символьных переменных oldчисловыми значениями из списка new: » subs(u,[a s],[3 2]) ans = 0.9808 Математический анализ 6.3.1. Функция limit – предел функции одной переменной Система MATLAB реализует важную математическую операцию – вычисление предела, т е. Синтаксискоманды ( limit(f) – предел при первый замечательный предел: » x=sym('x'); limit(sin(x)/x) ans = второй замечательный предел » limit((1+x)^(1/x)) ans = Exp(1) » limit((x-sin(x))/x^3) ans = 1/6 » limit(x^x) ans = limit(f,a)– предел при » limit((pi-2*x)*tan(x),pi/2) ans = limit(f,x,a) – явный предел при » syms t x; » limit((1+2*t/x)^(3*x),x,inf) ans = exp(6*t) limit(f,x,a,’left’), limit(f,x,a,’right’) – вычисление соответственно левого и правого пределов. » syms x a » v=[(1+a/x)^x,exp(-x)]; limit(v,x,inf,'left') ans = [ exp(a), 0] Упражнение. Найти пределы
6.3.2. Функция diff – дифференцирование функции одной переменной Синтаксис функции: diff(f) – автоматическое определение переменной с помощью findsym(f) и дифференцирование – » x=sym(‘x’) » diff(sin(x)^2); ans = 2*sin(x)*cos(x) » simple(ans) ………………. ans = sin(2*x) % Предшествующие преобразования условно опущены
diff(f,v)–дифференцирование по переменной v, » syms x y, u=x^y; v=diff(u,x), w=diff(u,y) v = x^y*y/x w = x^y*log(x) » simplify(v) ans = x^(y-1)*y diff(f,x,n)–производная n-го порядка » for n=1:7, clc, n, diff(x^6,n), pause, end Упражнение. Найти производную функции 6.3.3. Функция int – интегрирование функции одной переменной Синтаксис функции: int(f)– вычисление первообразной после автоматического определения независимой переменной x, т.е. » int(1/cos(x)) ans = log(sec(x)+tan(x)) » int(1/x) ans = Log(x) int(f,v)– интегрирование по переменной v, т.е. » u=x^y; » int(u,x) ans = x^(y+1)/(y+1) » int(u,y) ans = 1/log(x)*x^y » int([1-exp(-x), x^2]) ans = [ x+exp(-x), 1/3*x^3] int(f,a,b), int(f,v,a,b)– определенный интеграл, т.е. » int(exp(-x^2),-inf,inf) % ans = pi^(1/2) % Упражнение.Вычислить интеграл 6.3.4. Функция symsum – суммирование членов рядов Синтаксис функции: symsum(s) – суммирование ряда с общим членом s(k) в пределах от 0 до k-1. Сумма натуральных чисел от 0 до k-1; » syms k » u=symsum(k) ans = 1/2*k^2-1/2*k » factor(u) % или simple(u) ans = 1/2*k*(k-1) symsum(s,kl,ku)– суммирование ряда по индексу k от kl до ku, т.е. » symsum(k,1,3) ans = сумма » symsum(k^2,1,5) ans = сумма » symsum(1/k^2,1,inf) ans = 1/6*pi^2 сумма » symsum(x^k/sym('k!'),k,0,inf) ans = Exp(x) С помощью функции sym создано символьное выражение для факториала k!, поскольку символ ! не воспринимается системой MATLAB как знак факториала. Сумма » symsum((-1)^k/k,1,inf) ans = -log(2) » -log(2) ans = -0.6931 6.3.5. Функция taylor – разложение функции в ряд Тэйлора Разложение функции
который при Синтаксис функции: taylor(f)– возвращение по умолчанию шести членов ряда Маклорена; taylor(f,n)– возвращение разложения в ряд Маклорена, удерживается n-1членов; taylor(f,a) taylor(f,a,n)– то же для ряда Тэйлора. Пример: разложим функцию » syms x; » f=exp(-x); » u3=taylor(f,3) u3 = 1-x+1/2*x^2 » u6=taylor(f) u6 = 1-x+1/2*x^2-1/6*x^3+1/24*x^4-1/120*x^5 » u10=taylor(f,10) u10 = 1-x+1/2*x^2-1/6*x^3+1/24*x^4-1/120*x^5+1/720*x^6-1/5040*x^7+1/40320*x^8-1/362880*x^9 » x=1.0; » s3=subs(u3); s6=subs(u6); s10=subs(u10); » a=exp(-1) a = 0.3679 » disp(a-s3) -0.1321 » disp(a-s6) 0.0012 » disp(a-s10) E-007 Упражнение. Разложить в ряд Тэйлора функцию
Поиск по сайту: |
 . Предел может быть конечным числом (в том числе 0), а также
. Предел может быть конечным числом (в том числе 0), а также 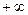 и
и  . В точках разрыва функции
. В точках разрыва функции  можно различать пределы слева:
можно различать пределы слева:  и справа:
и справа:  ; при равенстве этих пределов существует предел в точке a.
; при равенстве этих пределов существует предел в точке a.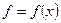 ):
): :
: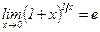 :
: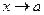 (предварительно с помощью функции findsym(f) определяется независимая переменная – в данном случае х),
(предварительно с помощью функции findsym(f) определяется независимая переменная – в данном случае х), ;
; 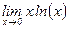 ;
; 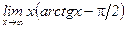 .
. ,
,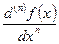 :
: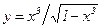 и вычислить ее значение при x=0.5. Ответ: 0.8591.
и вычислить ее значение при x=0.5. Ответ: 0.8591. ,
, ,
, ,
,

 и найти его значение при
и найти его значение при 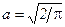 . Ответ: 1.0.
. Ответ: 1.0. , т.е.
, т.е. , т.е.
, т.е. , т.е.
, т.е.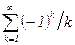 , т.е.
, т.е. в окрестности точки а имеет вид ряда Тэйлора
в окрестности точки а имеет вид ряда Тэйлора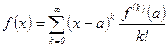 ,
,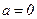 представляет собой ряд Маклорена
представляет собой ряд Маклорена  .
.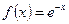 в ряд Маклорена, удерживая 6 (по умолчанию), 3 и 10 членов, вычислим значения функции при
в ряд Маклорена, удерживая 6 (по умолчанию), 3 и 10 членов, вычислим значения функции при  и сравним с точным:
и сравним с точным: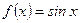 в окрестности точки
в окрестности точки 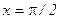 с точностью до 9 членов разложения.
с точностью до 9 членов разложения.