 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Краткая информация об объектно-ориентированном программировании
Практика и теория программирования не стоит на месте. В настоящее время наибольшей популярностью у профессиональных программистов пользуется объектно–ориентированное программирование (ООП). Эта технология предназначена в первую очередь для разработки больших программных продуктов (как, например, сам MATLAB). Нам с вами в основном приходится иметь дело с относительно простыми прикладными вычислительными задачами. Для них, как правило, достаточно владеть средствами структурного и модульного программирования. Однако в плане ликбеза – краткая информация. Главное отличие ООП от традиционных технологий программирования – использование объектов и классов. Когда-то единственным инструментом, позволяющим их использовать был язык программирования С++ (первоначальное название: С с классами). В настоящее время средства для работы с объектами и классами введены в большинство систем программирования. Имеются они и в языке программирования MATLAB’а. Вам очевидно известны основные типы данных, используемые в традиционных языках программирования: простые переменные, массивы, строки символов. Вероятно, встречались со структурами (записями). Все это тем или иным образом организованные данные. Объекты же отличатся тем, что помимо самих данных в них включаются и те действия (методы), которые могут производиться над этими данными. То есть тем самым включается дополнительная защита, не позволяющая делать с данными объекта несанкционированные действия. Классы, в некоторой степени, подобны типам переменных. То есть отдельный объект должен принадлежать к какому-то классу. Например, мы может дать объекту какое-то имя (например А) и указать, что он принадлежит к классу «квадратные матрицы». В описании класса должна быть указана структура данных, описывающих этот объект (например, n – размер матрицы, и n2 чисел – элементов матрицы), а также действия, которые можно выполнять с этим объектом (например, вычисление определителя и умножение на объект класса «вектор»). Для описания самих классов используется достаточно изощренная схема с наследованием. Например, можно описать как базовый класс «матрица общего вида». Далее, используя этот класс в качестве родительского, описать новые классы. Например, класс «квадратная матрица» и класс «вектор-столбец». Классы-«дети» наследуют все свойства классов-«родителей» и, как правило, имеют дополнительные свойства. В современных языках имеется богатая библиотека классов (например, MFC в C++). В общем, овладение ООП достаточно трудоемкая затея. Стоит ли к ней приступать, каждый должен решать сам. В качестве ориентира могу сказать следующее. Техника структурного программирования получила развитие тогда, когда обнаружилось, что написать программу размером более 1000 строк программного кода для человека практически нереально. Структурное и модульное программирование позволили увеличить этот размер до величины порядка 10000 строк. На мой взгляд, пока Ваши программы далеки от последнего размера, связываться с ООП нет необходимости.
Что еще почитать
Как Вы понимаете, для настоящего освоения техники программирования недостаточно ознакомиться с конспективными заметками вроде этих методичек. Если Вы почувствуете необходимость в углублении своих знаний и умений в качестве программиста, необходимы самостоятельная работа и изучение соответствующей литературы. К сожалению, большинство книг по программированию представляют собой описания конкретных языков программирования, их синтаксиса, используемых структур данных и т.п. Книг, обучающих собственно программированию, не много. В качестве одной из лучших книг, с которой можно начать знакомство с таким увлекательным занятием, как программирование, могу порекомендовать книгу Денни ванн Тассела «Стиль, разработка, эффективность, отладка и испытание программ». Помимо детального рассмотрения вопросов затронутых в этой и следующей методичке, в ней есть краткие, но очень полезные советы. Например
Задания
1. Программу для решения задачи предыдущего занятия напишите заново, используя технику пошаговой детализации. Сравните коды, перечислите отличия 2. Написать программу решения нелинейного уравнения, с использованием указанного метода (половинного деления, хорд, Ньютона, простых итераций). Кроме решения уравнения программа должна строить график функции на заданном отрезке. Результаты работы проверить с помощью функции fzero. Результаты оформить в виде отчета.
Справочная информация Как известно, далеко не всякое алгебраическое уравнение
может быть решено аналитически. Это относится к большинству трансцендентных уравнений и к алгебраическим уравнениям выше четвертого порядка. Однако точное решение уравнений на практике часто и не требуется. Чтобы считать задачу решенной, достаточно бывает отыскать значения корней с требуемой степенью точности. Для получения таких решений разработаны численные методы.
На втором этапе внутри выделенных отрезков вычисляются значения каждого из корней уравнения с заданной точностью. Для этого используются два основных итерационных подхода: сужение выделенного отрезка,содержащего корень, и последовательное уточнение первоначального приближения значения корня, взятого из выделенного отрезка.
Методы сужения отрезка [a, b], к которымотносятсяметод хорд, метод половинного деленияи др., не имеют ограничений на функцию f(x), присущих методам последовательного уточнения.
Метод половинного деления (метод бисекций)
Работа метода иллюстрируется на рис.2. Отрезок изоляции [a, b] корня делится пополам x0 = (a + b)/2 и в полученной точке вычисляется значение функции. Если f(x0) = 0, то корень найден и расчеты прекращают. В противном случае выбирается новый отрезок, содержащий корень уравнения, из отрезков [a, x0] и [x0, b]. На концах искомого отрезка функция f(x) должна иметь значения разного знака. Для этого проверяется условие f(a)f(x0) < 0.
Метод хорд
Идея метода состоит в замене функции f(x) внутри отрезка [a, b] линейной функцией. Точка пересечения x0графика линейной функции и оси абсцисс принимается за значение одной из границ нового отрезка изоляции корня, который выбирается аналогично методу половинного деления. Далее процесс повторяется и находится x1 - точка пересечения графика линейной функции нового отрезка с осью абсцисс. Иллюстрацией этого алгоритма является рис.3. Процесс поиска корня продолжается до тех пор, пока не будет выполнено условие, задающее погрешность его определения. Для расчета на каждом шаге координаты точки пересечения графика линейной функции и оси абсцисс используются выражения вида:
или
Методы последовательного уточнения начального приближенного значения корня. К этим методам относятся методпростых итераций, метод Ньютона и ряд других. Ониобладают высокойэффективностью, но их применение связано с рядом ограничений, накладываемых на свойства функции f(x).
Метод простых итераций
Метод основывается на приведении исходного уравнения к форме
Это преобразованиеможет быть выполнено многими способами. Например, уравнение
может быть преобразовано как x= e-x или x = ln |1/x|. Далее процесс уточнения корня строится по следующей итерационной схеме
……………
…………… где x0 - первоначальное приближенное значение корня на отрезке [a, b]. Если последовательностьзначений xk (k = 0, 1, 2, ...) имеетконечный предел, то итерационный процесс сходится к точному значению корня x*за бесконечно большое число шагов. Поэтому итерации завершают при выполнении одного из условий:
Процесс уточнения корня уравнения методом простых итераций может быть проиллюстрирован графически. Как видно на рис.4, для выбранной на отрезке [a, b] начальной точки x0 вычисляется значение функции j (x0). Абсцисса этой точки с помощью графика функции y = x преобразуетсявновое приближение переменной x1. Далее процесс повторяется, и находятся значения x2, x3, ..., xk,... до тех пор, пока не будет выполнено условие завершения итерационного процесса по заданной погрешности вычисления корня e. В данном случае итерационный процесс сходится и заданная погрешность вычисления корня достижима. На рис.5 показана ситуация, когда метод итераций расходится. Каждое новое значение xk отстоит все дальше от точного решения уравнения x*и заданная погрешность вычисления недостижима. Такая ситуация характерна для неудачного преобразования уравнения f(x) = 0 к уравнению x = j (x). В методе итераций рекомендуется преобразовывать исходное уравнение, основываясь на теореме о его сходимости, которая гласит: есливо всех точках отрезка изоляции [a,b] корня уравнения x = j (x)функция j (x) удовлетворяет условию |j¢(x)| < 1, то итерационный процесс сходится к точному значению корня x*для любого x0 из отрезкаизоляции. Исходя из вышесказанного, можно указать еще один способ преобразования исходного уравнения к форме, требуемой методом итераций. Исходное уравнение f(x) = 0 равносильно уравнению x = x + lf(x), где l - отличная от нуля произвольная постоянная. Эта постоянная выбирается из условия сходимости метода |j¢(x)| < 1, считая j (x) = x + l f(x). В этом случае условие сходимости переписывается в виде: |1+l f¢(x)| < 1 , и условие на допустимое значение параметра l приобретает вид -2<l f¢(x)<0 , что дает весьма широкий интервал значений. Это позволяет использовать приближенную оценку производной f¢(x) в окрестности искомого корня, которую можно получать, например, из построенного графика функции f(x). Очевидно, что для каждого корня уравнения следует формировать соответствующую ему функцию j (x) на основе подобранного значения параметра l. Удобно, например, выбирать его в середине интервала допустимых значений: l=-1/ f¢(x) .
Метод Ньютона
В данном методе каждое новое приближение к значению корня уравнения f(x) = 0 ищется по следующей итерационной схеме
………………….
…………………. где x0 - первоначальноеприближенноезначение корня на отрезке [a,b]. Графическая интерпретация работы метода Ньютона представлена на рис.4. Из точки на кривой y = f(x), имеющей абсциссу x0, проводится касательная до пересечения с осью 0x и абсцисса точки пересечения принимается за новое приближение x1 значения корня уравнения f(x) = 0. В случае сходимости последовательности вычисляемых значений x0, x1, ...,xk,... процесс продолжается до тех пор, пока не выполнится условие его завершения по заданной погрешности определения корня e. Чтобы последовательность приближений x0, x1, ..., xk, ... сходилась к значению корня x*, необходимо и достаточно выполнение условий следующей теоремы. Еслив окрестности корня x* функция f(x) имеет непрерывные производные f¢(x) и f¢¢(x), для которых справедливо неравенство
тоитерационный процесс сходится к точному значению корнядля любого x0 из [a, b].
Поиск по сайту: |
 ,
(0 £ x £ 8)
,
(0 £ x £ 8)
 , (0 £ x £ 2,5)
, (0 £ x £ 2,5)
 ,
(0 £ x £ 2)
,
(0 £ x £ 2)
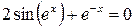 ,
(0 £ x £ 2)
,
(0 £ x £ 2)
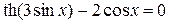 ,
(0 £ x £ 8)
,
(0 £ x £ 8)
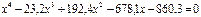 , (2 £ x £ 8)
, (2 £ x £ 8)
 ,
(1 £ x £ 6)
,
(1 £ x £ 6)
 , (0 £ x £ 8)
, (0 £ x £ 8)
 , (0 £ x £ 8)
, (0 £ x £ 8)
 , (0 £ x £ 3)
, (0 £ x £ 3)
 ,
(0 £ x £ 4)
,
(0 £ x £ 4)
 ,
(0 £ x £ 6)
,
(0 £ x £ 6)
 ,
(0 £ x £ 8)
,
(0 £ x £ 8)
 ,
(0 £ x £ 2)
,
(0 £ x £ 2)
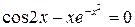 ,
(0 £ x £ 4)
,
(0 £ x £ 4)
 , (2 £ x £ 4)
, (2 £ x £ 4)
 ,
(0 £ x £ 3,5)
,
(0 £ x £ 3,5)
 ,
(2 £ x £ 15)
,
(2 £ x £ 15)
 ,
(0 £ x £ 10)
,
(0 £ x £ 10)
 , (2 £ x £ 12)
, (2 £ x £ 12)
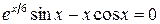 ,
(3 £ x £ 12)
,
(3 £ x £ 12)
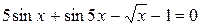 , (0 £ x £ 8)
, (0 £ x £ 8)
 ,
(0 £ x £ 4)
,
(0 £ x £ 4)
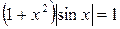 ,
(0 £ x £ 4)
,
(0 £ x £ 4)
 ,
(0 £ x £ 8)
,
(0 £ x £ 8)
 (0 £ x £ 4)
(0 £ x £ 4)
 ,
(0 £ x £ 4)
,
(0 £ x £ 4)
 ,
(0 £ x £ 4)
,
(0 £ x £ 4)
 ,
(0 £ x £ 4)
,
(0 £ x £ 4)
 ,
(2 £ x £ 10)
,
(2 £ x £ 10)

 Решение нелинейных уравнений осуществляется в два этапа. На первом этапе производится отделение корней, то есть поиск достаточно малых отрезков, каждый из которых содержит единственный корень уравнения. Для этого используется график функции y = f(x), точки пересечения которого с осью абсцисс являются корнями исходного уравнения. Случай, когда корнем уравнения является точка касания графика и оси абсцисс здесь не рассматривается. Это позволяет выделить отрезки [a,b], содержащие только один корень (см. рис 1). При этом для непрерывной функции f(x) будет выполняться неравенство f(a) f(b) < 0.
Решение нелинейных уравнений осуществляется в два этапа. На первом этапе производится отделение корней, то есть поиск достаточно малых отрезков, каждый из которых содержит единственный корень уравнения. Для этого используется график функции y = f(x), точки пересечения которого с осью абсцисс являются корнями исходного уравнения. Случай, когда корнем уравнения является точка касания графика и оси абсцисс здесь не рассматривается. Это позволяет выделить отрезки [a,b], содержащие только один корень (см. рис 1). При этом для непрерывной функции f(x) будет выполняться неравенство f(a) f(b) < 0.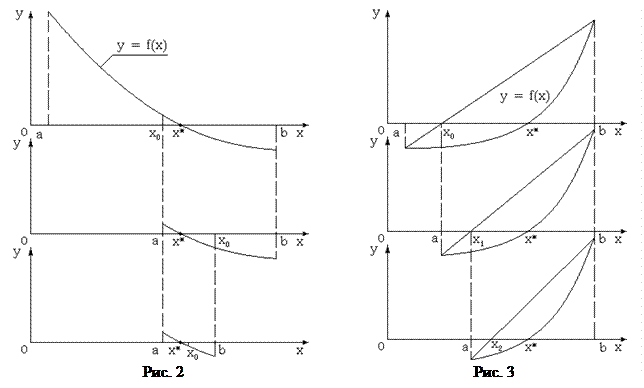 При его выполнении в качестве нового отрезка принимается отрезок [a, x0], в противном случае - [x0, b]. Процесс сужения отрезка продолжается до тех пор, пока его длина не станет меньше наперед заданного значения абсолютной погрешности e или не будет выполнено условие по относительной погрешности определения корня. При этом за значение корня принимается либо одна из границ суженного отрезка [a, b], либо его середина.
При его выполнении в качестве нового отрезка принимается отрезок [a, x0], в противном случае - [x0, b]. Процесс сужения отрезка продолжается до тех пор, пока его длина не станет меньше наперед заданного значения абсолютной погрешности e или не будет выполнено условие по относительной погрешности определения корня. При этом за значение корня принимается либо одна из границ суженного отрезка [a, b], либо его середина.
 .
.




 или
или  ,
, где e - требуемая абсолютная или относительная погрешность определения корня, соответственно. Однако, может случиться так, что последовательность значений xk (k = 0, 1, 2, ...) не имеет предела. В этом случае метод расходится, и описанная итерационная схема не может быть применена для решения уравнения.
где e - требуемая абсолютная или относительная погрешность определения корня, соответственно. Однако, может случиться так, что последовательность значений xk (k = 0, 1, 2, ...) не имеет предела. В этом случае метод расходится, и описанная итерационная схема не может быть применена для решения уравнения.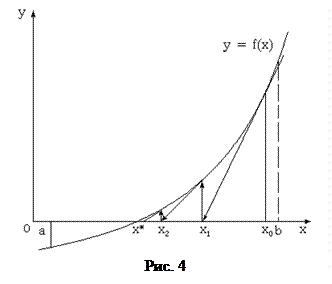



 ,
,