 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Преобразование энергетических характеристик детерминированных сигналовСтр 1 из 2Следующая ⇒
Рассмотрим преобразования энергетических характеристик детерминированных сигналов длительности Т в линейных стационарных системах (каналах). Учитывая определение СПМ (спектральная плотность мощности), можно выразить связь между этими характеристиками на выходе и входе детерминированного линейного стационарного канала:
Средние мощности сигналов на входе и выходе системы определяются соотношениями
ФК (функция корреляции) Bx(τ) сигнала x(t) и его СПМ Gx(f) связаны парой преобразований Фурье. Если ввести в рассмотрение ФК для ИХ системы (канала):
ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ В ДЕТЕРМИНИРОВАННЫХ ЛИНЕЙНЫХ КАНАЛАХ (связь м/у ИХ и передаточной характеристиками) Исследование преобразований случайных процессов при их прохождении через динамические системы связано с решением задач двух типов: определение корреляционной функции (спектральной плотности мощности) отклика Y(t) на выходе системы, заданной своими характеристиками, по данной корреляционной функции (или спектральной плотности мощности) входного воздействия X(t); определение многомерного распределения вероятностей отклика Y(t) на выходе системы по многомерному распределению входного воздействия X(t). Вторая из указанных задач является более общей. Из её решения, очевидно, может быть получено решение первой задачи. Рассмотрим решение только первой задачи и лишь укажем пути решения второй, более сложной задачи. Так, можно утверждать, что если полоса частот Fx, занимаемая входным случайным процессом X(t), много шире полосы пропускания ∆F данной линейной системы, то распределение выходного случайного процесса Y(t) имеет тенденцию приближаться к гауссовскому. Действительно, в стационарной детерминированной линейной системе с финитной т.е. ограниченной во времени пределами 0...τп ИХ g(t) отклик
Шаг дискретизации ∆τ можно выбрать равным интервалу корреляции входного процесса 1/Fx. Допустим, что входной процесс центрирован Для стационарных случайных процессов существует пара преобразований Фурье между ФК Bx(τ) и By(τ) процессов X(t) и Y(t) и их СПМ Gx(f), Gy(f). Поскольку для стационарной линейной системы и при случайных стационарных воздействиях справедливо соотношение (4.38), то ФК выходного стационарного процесса Y(t)
Можно показать , что ФК отклика детерминированной параметрической системы на стационарные входные воздействия X(t) определяется формулой
т.е. в данном случае выходной процесс, вообще говоря, нестационарен. Случайные линейные каналы связи и их характеристики, особенности проводных и радиоканалов, замирания сигналов. Флуктуационные, сосредоточенные и импульсные помехи в канале, их вероятностные характеристики. Случайный линейный канал. В самом общем виде линейную систему (или линейный канал) можно описать случайной ИХ G(t,τ), имеющей тот же смысл, что. и g(t,τ) в (4.7), но представляющей случайную функцию двух аргументов: t (момента наблюдения реакции) и τ (времени, прошедшего с момента подачи δ-импульса на вход цепи). Случайный линейный канал можно характеризовать также случайной передаточной функцией переменных w и t
Можно показать, что функция корреляции процесса Y(t) на выходе случайного канала с характеристикой (4.41) при подаче на вход стационарного процесса X(t) определяется выражением
где Остановимся подробнее на моделях, с которыми чаще всего приходится встречаться. Обобщая модель (4.25) для случайного входного воздействия X(t), получаем Y(t)=γX(t-τ), где параметры τ и (или) γ флуктуируют. Обычно такие флуктуации в проводных линиях связи вызываются изменениями внешних условий и происходят чрезвычайно медленно (это значит, что за время длительности отсчёта ого интервала ∆ = 1/2F, где F — ширина спектра сигнала, параметры канала не успевают заметно изменяться) и в очень небольших относительных пределах. В радиоканалах при многолучевом распространении волн, в гидроакустических каналах и других флуктуации выражены более заметно. Если входной сигнал узкополосный, его удобно представить в квазигармонической форме: X(t) =A(t)cos[wot+Ф(t)], где A(t) и Ф(t) — медленно меняющиеся функции. Поэтому при достаточно малой задержке τ можно в первом приближении считать A(t — т) ≈ A(t) и Ф(t — т) ≈ Ф (f), а выходной сигнал (4.43) записать следующим образом:
где θ = -wot - фазовый сдвиг в канале, a Таким образом, при узкополосном сигнале малая задержка сводится к некоторому сдвигу фазы. Важно отметить, что даже при очень малых относительных флуктуациях времени задержки τ фазовый сдвиг θ (из-за больших значений wo) может изменяться в очень больших пределах. Для этого достаточно выполнения условия ∆τ >> 1/f0, где ∆τ - среднеквадратическое отклонение задержки, f0 — средняя частота спектра сигнала. Более сложный случай имеет место, когда сигнал проходит по параллельным путям от входа Канала к его выходу (рис. 4.2), так что на выходе каждого пути сигнал имеет вид (4.44), но значения γ и τ для разных путей различны и к тому же в небольших пределах флуктуируют. Для пояснения замираний рассмотрим передачу по каналу (см. рис. 4.2) гармонического сигнала с единичной амплитудой u(t) = Re(ejwt). На выходе сигнал
где L — число путей (подлучей, попадающих в точку приёма); γl — коэффициент передачи по l-му подлучу; τl— время распространения l-го подлуча;
Передаточная функция в общем случае зависит от частоты. Если учесть, что вследствие хаотических перемещений отражателей значения γl и τl флуктуируют, то Важной характеристикой канала с замираниями является распределение вероятностей комплексной передаточной функции С другой стороны, согласно (4.45) Откуда Для случая, когда все γl одного порядка и фазовые сдвиги достаточно велики, легко показать, что X и Y имеют одинаковые дисперсии Во многих каналах замирания отличаются от рэлеевских. Иногда в одном из подлучей коэффициент передачи γl, значительно больше, чем в других, и можно сказать, что помимо диффузно отражённых подлучей в место приёма приходит и регулярный (не замирающий) луч. В этом случае коэффициент передачи канала Здесь В общем случае, когда четырёхпараметрическое распределение модуля и фазы замирающего сигнала (общая гауссовская модель канала). Если по однолучевому каналу с замираниями передаётся относительно узкополосный сигнал, а среднеквадратическое отклонение запаздывания ∆τ в отдельных подлучах удовлетворяет условию ∆τ<<1/Fc (4.46) где Fc — ширина спектра сигнала, то изменения начальных фаз на разных частотах со в спектре сигнала, равные w∆τ, почти одинаковы. При этом все составляющие спектра сигнала замирают "дружно", т.е. их амплитуды и фазы изменяются одинаково. Такие замирания называются общими или гладкими. Быстрота изменений во времени комплексного случайного процесса
Поиск по сайту: |
 (4.38)
(4.38)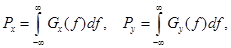
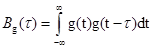 , то, используя обобщённую формулу Рэлея (2.137) и соотношение (4.8), можно получить
, то, используя обобщённую формулу Рэлея (2.137) и соотношение (4.8), можно получить т.е. ФК системной характеристики g(t) и коэффициент передачи системы по мощности K2(f) связаны парой преобразований Фурье. Используя спектральное соотношение (4.38), можно утверждать, что ФК выходного сигнала y(t) определяется свёрткой ФК входного сигнала x(t) и ФК импульсной характеристики системы
т.е. ФК системной характеристики g(t) и коэффициент передачи системы по мощности K2(f) связаны парой преобразований Фурье. Используя спектральное соотношение (4.38), можно утверждать, что ФК выходного сигнала y(t) определяется свёрткой ФК входного сигнала x(t) и ФК импульсной характеристики системы  .
. (4.39)
(4.39) ,тогда центрирован и выходной процесс. Сечение выходного процесса Y(t) в любой момент времени t определяется согласно (4.39) N слагаемыми суммы. В предельном случае, если на вход канала воздействует белый шум, у которого ширина спектра бесконечна (не совпадающие во времени отсчёты не коррелированы), а канал имеет ограниченную полосу пропускания, то N→∞и выходной процесс будет строго гауссовским.
,тогда центрирован и выходной процесс. Сечение выходного процесса Y(t) в любой момент времени t определяется согласно (4.39) N слагаемыми суммы. В предельном случае, если на вход канала воздействует белый шум, у которого ширина спектра бесконечна (не совпадающие во времени отсчёты не коррелированы), а канал имеет ограниченную полосу пропускания, то N→∞и выходной процесс будет строго гауссовским.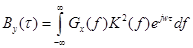
 (4.40)
(4.40) (4.41)
(4.41)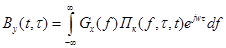 (4.42)
(4.42)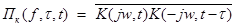 - системная характеристика случайного канала. Для детерминированного канала
- системная характеристика случайного канала. Для детерминированного канала 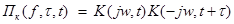 , и из (4.42) следует (4.40).
, и из (4.42) следует (4.40). (4.44)
(4.44)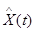 — процесс, сопряжённый с X(t) по Гильберту.
— процесс, сопряжённый с X(t) по Гильберту.
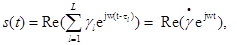 (4.45)
(4.45)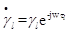 — комплексный коэффициент передачи по l-му лучу;
— комплексный коэффициент передачи по l-му лучу; 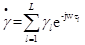 — комплексная амплитуда выходного сигнала, которая в данном случае по определению равна передаточной функции канала.
— комплексная амплитуда выходного сигнала, которая в данном случае по определению равна передаточной функции канала.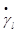 зависит также от времени, представляя собой случайную функцию (мультипликативную помеху)
зависит также от времени, представляя собой случайную функцию (мультипликативную помеху)  . Во многих случаях эта функция флуктуирует значительно быстрее, чем величины γl и τl.
. Во многих случаях эта функция флуктуирует значительно быстрее, чем величины γl и τl.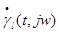 и в первую очередь её модуля
и в первую очередь её модуля 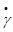 . Для определения этого распределения представим
. Для определения этого распределения представим  , где
, где 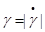 и θ - соответственно модуль и аргумент передаточной функции, которые также являются случайными функциями t и w, a X = γcosθ и Y= γsinθ— квадратурные составляющие.
и θ - соответственно модуль и аргумент передаточной функции, которые также являются случайными функциями t и w, a X = γcosθ и Y= γsinθ— квадратурные составляющие.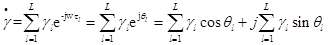
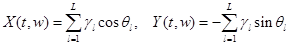
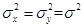 , а их математические ожидания mх = mу = 0. Здесь одномерное распределение вероятности γ является рэлеевским:
, а их математические ожидания mх = mу = 0. Здесь одномерное распределение вероятности γ является рэлеевским:  .
. подчиняется обобщённому распределению Рэлея
подчиняется обобщённому распределению Рэлея 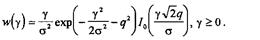
 - отношение средних мощностей регулярной и флуктуирующих составляющих.
- отношение средних мощностей регулярной и флуктуирующих составляющих.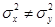 и mх ≠ 0 и mу ≠ 0, получается так называемое
и mх ≠ 0 и mу ≠ 0, получается так называемое (при фиксированной частоте) или, как говорят, скорость замираний сигнала характеризуется временем корреляции τкор квадратурных компонент X(t, w) и Y(t, w) или шириной спектра замираний
(при фиксированной частоте) или, как говорят, скорость замираний сигнала характеризуется временем корреляции τкор квадратурных компонент X(t, w) и Y(t, w) или шириной спектра замираний 