 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Средняя геометрическая ⇐ ПредыдущаяСтр 3 из 3
где n – число единиц в совокупности.
Предприятиями были осуществлены следующие инвестиции в основные фонды: Таблица 6.6
Найдем средний размер инвестиций. Поскольку колеблемость признака довольно значительная и данные несгруппированы, воспользуемся формулой средней геометрической простой:
Средняя квадратическая и другие степенные средние более высоких порядков Если мы подставим в формулу средней степенной т = 2, то получим среднюю квадратическую: взвешенную (для сгруппированных данных): простую (для несгруппированных данных): Средняя квадратическая величина широко применяется при оценке вариации признака, а также в многомерных статистических методах. Кроме того, прикладное значение имеет расчет степенных средних и более высоких порядков, например, при изучении характеристик распределения случайных величин. Формулы для их вычисления получаются при подстановке в качестве т соответствующего показателя степени. Мода. Мода(Мо) - это наиболее часто встречающееся значение признака, или, говоря иначе, значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по-разному. В зависимости от того, равны интервалы между собой или нет, применяют тот или иной подход к определению моды. В дискретных вариационных рядах для определения моды не требуется специальных вычислений: значение признака, которому соответствует наибольшая частота, и будет значением моды. 6. 5.По представленным результатам проведения экзамена по статистике определим моду. Таблица 6.7
Здесь наибольшая частота – 10, она принадлежит варианте со значением 3, значит, Мо = 3. Таким образом, самой распространенной оценкой, полученной студентами на экзамене, была "тройка". Для определения моды в интервальных вариационных рядах с равными интервалами сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем ведут расчет по формуле
где xMo- нижняя граница модального интервала; d - величина интервала; fMo – частота модального интервала; fMo-1 – частота интервала, предшествующего модальному; fMo+1 – частота интервала, следующего за модальным. 6. 6.Имеются данные по группе банков. Таблица 6.8
Определим модальный размер выданных кредитов: 1) модальным является интервал 60—80, так как ему соответствует наибольшая частота (21); 2) нижняя граница модального интервала хМо = 60; величина интервала d = 20 (80 - 60 = 20); частота модального интервала fМо = 21; частота интервала, предшествующего модальному, fМо-1= 15; частота интервала, следующего за модальным, fМо+1 = 12. Тогда, подставив в формулу соответствующие величины, получим:
Если интервалы вариационного ряда не равны между собой, то для определения моды необходимо проделать следующие действия; 1) для каждого интервала на основе частот (fi) и длин интервалов (di) рассчитать величину 2) по наибольшей абсолютной плотности распределения найти модальный интервал; 3) определить значение моды по формуле
где xMo – нижняя граница модального интервала; dMo – величина модального интервала; рМо - абсолютная плотность модального интервала; pMo-1 – абсолютная плотность интервала, предшествующего модальному; pMo+1 – абсолютная плотность интервала, следующего за модальным. 6. 7.Имеются данные по группе коммерческих банков : Таблица 6.9
Определим модальное значение размера кредитной ставки под краткосрочные кредиты.
Задачи и упражнения 6.2.1.По коммерческой фирме имеются следующие данные об объеме товарооборота за год: Таблица 6.21
Определите: 1) Средний товарооборот фирмы. 2) Структурные средние Мо и Me 3) Сделайте выводы по рассчитанным показателям
6.2.4Используя данные, приведенные ниже в таблице о выпуске продукции промышленной компанией за отчетный год , рассчитайте необходимые статистические показатели. Таблица 6.22
Определите: а) средний процент выполнения плана по выпуску продукции; б) средний дельный вес продукции высшего качества
Поиск по сайту: |
 Если минимальное и максимальное значения признака резко отличаются друг от друга, что возникает при существенной вариации показателя в совокупности, либо, если мы имеем данные, представляющие собой отношения двух показателей, например, индексы или коэффициенты роста, то для нахождения среднего значения используется формула средней геометрической, Для несгруппированных данных (при отсутствии частот) или для сгруппированных данных с равными частотами применяется средняя геометрическая простая
Если минимальное и максимальное значения признака резко отличаются друг от друга, что возникает при существенной вариации показателя в совокупности, либо, если мы имеем данные, представляющие собой отношения двух показателей, например, индексы или коэффициенты роста, то для нахождения среднего значения используется формула средней геометрической, Для несгруппированных данных (при отсутствии частот) или для сгруппированных данных с равными частотами применяется средняя геометрическая простая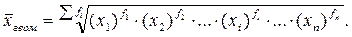 Для сгруппированных данных с неравными частотами применяется средняя геометрическая взвешенная
Для сгруппированных данных с неравными частотами применяется средняя геометрическая взвешенная


 3
3


 которая называется абсолютной плотностью распределения;
которая называется абсолютной плотностью распределения;

 Модальным является интервал 25-40, так как у него наибольшая плотность распределения (0,93). Значение моды равно:
Модальным является интервал 25-40, так как у него наибольшая плотность распределения (0,93). Значение моды равно: