 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Непрерывная случайная величина ⇐ ПредыдущаяСтр 2 из 2
Случайная величина X называется непрерывной, если ее функция распределения F(x) непрерывна на всей числовой оси. Для непрерывной случайной величины X при любом x0 Р(Х = х0) = 0.
Плотностью вероятности непрерывной случайной величины называют производную от функции распределения :
f(x)=F`(x).
Свойства плотности вероятности: 1) f(x)≥0 2) Вероятность того, что непрерывная случайная величина X примет в результате испытания значение в интервале (а,b), равна
3) Если плотность вероятности случайной величины X известна и равна f(x) то функцию распределения можно найти по формуле:
4) Имеет место равенство
Числовыми характеристиками непрерывных случайных величин являются математическое ожидание, дисперсия и среднее квадратичное отклонение, которые вычисляются по следующим формулам:
При этом предполагается, что несобственный интеграл сходится абсолютно
или
3.1 Задача. Случайная величина X задана функцией распределения
Найти: а) плотность вероятности; б) вероятность того, что случайная величина X примет значение в интервале (0; π/6). Решение. а) плотность вероятности равна первой производной от функции распределения:
Заметим, что при x=0 производная F(x) не существует. б) Искомая вероятность равна определенному интегралу в пределах от 0 до π/6 от плотности вероятности:
Эту вероятность можно найти и другим способом, используя 3) свойство функции распределения
3.2 Задача. Известна плотность вероятности случайной величины
Найти: а) коэффициент a; б) функцию распределения F(x). Решение . а) Известно, что
Поэтому,
Отсюда
б) Найдем функцию распределения F(x). Известно, что
Рассмотрим промежуток
Пусть
Пусть x>π/2. Тогда
Таким образом
Случайная величина X называется равномерно распределенной на отрезке [a; b], если ее плотность вероятности имеет вид:
Говорят, что случайная величина X подчиняется нормальному закону распределения, если ее плотность вероятности имеет вид:
где a – произвольный, а σ – положительный параметры. Для нормально распределенной случайной величины M[X]=a, D[X]= Вероятность попадания в заданный интервал (α; β) нормально распределенной случайной величины определяется формулой
где Φ(x) – функция Лапласа. Непрерывная случайная величина X имеет показательное распределение если ее плотность вероятности имеет вид:
где λ – параметр распределения. Можно показать, что M[X]=1/λ, D[X]=1/ Отметим, что показательное распределение широко применяется в приложениях, в частности, в теории надежности. Предлагаем для самостоятельного решения следующие задачи: 3.3 Дана функция распределения непрерывной случайной величины X:
где a>0. Найти плотность вероятности f(x). 3.4 Дана функция распределения случайной величины X:
а) Найти плотность вероятности f(x) и построить ее график. б) Исследуя график функции y=f(x), доказать, что математическое ожидание случайной величины равно нулю. 3.5 Дана функция распределения случайной величины X:
а) Найти плотность вероятности f(x). б) Найти вероятность того, что в результате испытания случайная величина попадает в интервал (-0, 5, 0). (0,5) 3.6 Плотность вероятности случайной величины X имеет вид:
где a>0. а) Найти параметр a. б) Построить график f(x). в) Найти P(1<x<2). ( а)2; в)0,75) 3.7 Случайная величина X имеет плотность вероятности
Найти функцию распределения F(x), построить ее график и найти (по графику) P( 3.8 Дана плотность вероятности случайной величины X:
Найти функцию F(x). 3.9 Случайная величина X задана функцией распределения
Найти вероятность того, что в результате испытания примет значение X<0,2; X<3; X 3.10 Случайная величина X задана плотностью вероятности f(x)=1/2x-5 на отрезке [10;12], вне этого интервала f(x)=0. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X. (34/3; 1/3; ≈0,526)
Варианты контрольных работ по темам «Случайные события» и «Случайные величины»
Вариант первый
1.В магазин поставляют изделия две фабрики. В продукции первой из них 90% стандартных изделий, второй - 80%. Известно, что во всей стандартной продукции магазина количество изделий фабрик относятся как 27:8. Изделие, отобранное случайным образом из всей продукции, оказалось нестандартным. Найти вероятность того, что оно изготовлено на второй фабрике. 2. Каждый выстрел в тире стоит 20 руб., за каждое попадание в цель выплачивается вознаграждение - 30 руб. Стрелок произвел 6 выстрелов. Какова вероятность того, что он останется в выигрыше, если вероятность попадания при каждом выстреле равна 0,7? 3. Вероятность того, что стиральная машина потребует ремонта в течение гарантийного срока равна 0,01. Найти вероятность того, что из 500 стиральных машин в течение гарантийного срока потребуют ремонта: а) три машины; б) не менее одной машины. 4.Среди купленных семи билетов - три билета в партер. Наудачу взяли 4 билета. Составить закон распределения числа билетов в партер среди взятых. Найти функцию распределения этой случайной величины. 5.Ошибки измерений некоторой величины подчинены нормальному закону с плотностью вероятности φ(х)= Проведено 1000 независимых измерений. Найти вероятность того, что не менее чем при 880 из них будет выполнено условие |x| ≤ 1,65.
Вариант второй
1.При первом выстреле вероятность попадания первого стрелка в движущуюся мишень равна 0,8, второго - 0,9. При втором выстреле эта вероятность уменьшается на 0,2 для каждого стрелка. Найти вероятность того, что в мишени будет не менее двух пробоин, если каждый из стрелков сделал два выстрела. 2.Найти такое число k, чтобы с вероятностью 0,9 можно было бы ожидать, что среди 900 новорожденных будет не менее k мальчиков. Вероятность рождения мальчика принять равной 0,515. 3.В коробке среди пяти деталей - две окрашенные. Детали извлекаются последовательно до извлечения обеих окрашенных деталей (после чего извлечения прекращаются). Составить закон распределения случайной величины Х - числа извлеченных деталей. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины. 4.Функция распределения непрерывной случайной величины х имеет вид F (х) = 5.Вероятность своевременной оплаты телефонной квитанции равна 0,85. Оценить вероятность того, что из 50 квитанций число своевременно оплаченных будет: а) от 39 до 46; б) не менее 45.
Вариант третий
1. Из 12 акций 3 принадлежат первому предприятию, 4 - второму и 5 - третьему. Пусть X, Y,Z- числа акций соответственно первого, второго и третьего предприятий среди двух акций, случайно отобранных из общего числа. Найти вероятность Р(Х = 1), Pr-t (X - 1), PY.2 (Х= 1). Выяснить, являются ли события (Х= 1) и (У- 1) независимыми. 2. При данном технологическом процессе в среднем k% изделий удовлетворяют стандарту. Найти вероятность того, что в партии из n изделий будет: а) 40 бракованных, если k - 80%, n - 200; б) менее 3-х бракованных, если k - 99,2%, n = 100. 3.Закон распределения случайной величины X имеет вид:
Случайная величина Y биномиально распределена с параметрами n=2, р=0,4.Составить закон распределения случайной величины Z=2X+ Y, полагая, что X и Y- независимы. Проверить выполнение свойства дисперсии: D(Z) =4D(X) + D(Y) . 4.Функция распределения непрерывной случайной величины X имеет вид:
где а и b - некоторые числа. Найти значения параметров а и Ь, если Р(Х> 1) =1/8. Вычислить Р(1 5.Средний расход воды на животноводческой ферме составляет 1000 л в день, а среднее квадратическое отклонение этой случайной величины не превышает 200 л. Оценить вероятность того, что расход воды на ферме в наудачу избранный день не превысит 2000 л, используя: а) лемму Чебышева (неравенство Маркова); б) неравенство Чебышева.
Вариант четвертый 1.На карточках написаны буквы, образующие слово «КОМБИНАТОРИКА», две карточки из этого набора утеряны. Наудачу извлекается одна карточка. Какова вероятность того, что на ней окажется гласная буква? 2.Одновременно бросаются три игральные кости. Найти вероятность того, что сумма выпавших очков будет не менее 16-ти. 3.Вероятность того, что прибор, случайно выбранный из партии, нуждается в дополнительной регулировке, равна 0,05. Если при выборочной проверке обнаруживается, что не менее 6% отобранных приборов нуждаются в регулировке, то вся партия будет возвращена для доработки. Найти вероятность того, что партия будет возвращена, если контролю будет подвергнуто 500 приборов из этой партии. 4.Имеется пять ключей, из которых два подходят к замку. Составить закон распределения числа X проб при открывании замка, если использованный ключ в последующих пробах не участвует. Найти функцию распределения случайной величины X, ее математическое ожидание и дисперсию. 5.Плотность распределения непрерывной случайной величины X имеет вид: φ(х)={
и равна 0 в остальных случаях, где а> 0. Найти значения параметра а, если М(Х)=1. Вычислить Р(Х> 2).
Вариант пятый
1.Пряжа поступает с трех станков, производительности которых относятся как 6:5:4. Вероятность того, что поступившая с первого станка пряжа будет высшего качества, равна 0,2, со второго - 0,3. Найти вероятность изготовления пряжи высшего качества на третьем станке, если среди продукции всех трех станков доля пряжи высшего качества равна 0,32. 2.Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность: а) попадания в цель при одном выстреле; б) менее трех попаданий при четырех выстрелах. З. Вероятность появления газовых раковин при отливке блока цилиндров автомобильного двигателя равна 0,1. Изготовлено 400 блоков цилиндров. Найти наибольшее отклонение частности отлитых блоков цилиндров с наличием газовых раковин от вероятности 0,1, которую можно гарантировать с вероятностью 0,9963. 4. При первичной поломке прибора, которая возможна с вероятнос- 5. При каком значении параметра а функция φ(х)= является плотностью распределения вероятности некоторой непрерывной случайной величины X? Найти вероятность того, что при двух измерениях этой случайной величины в обоих случаях ее значения будут принадлежать интервалу (-1; 1).
Вариант шестой
1. В коробке - 4 красных карандаша, 5 - синих и 6 - зеленых. Наудачу извлекаются три карандаша. Найти вероятность того, что: а) среди них не менее двух зеленых; б) все карандаши разных цветов. 2. При установившемся технологическом процессе изготавливается в среднем 15% бракованных шин. Сколько шин нужно взят- для проверки, чтобы с вероятностью 0,9876 доля бракованных шин оказалась бы в границах от 0,1 до 0,2? 3. Полоса препятствий некоторых соревнований содержит три рубежа различной сложности. Спортсмен преодолевает эти рубежи без штрафных очков с вероятностями 0,7, 0,4 и 0,2 соответственно. Составить закон распределения случайной величины X - числа рубежей полосы препятствий, пройденных без штрафных очков. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины. 4. Случайная величинах X нормально распределена, причем Р(Х> 2) =0,5 и Р(Х 5. Сколько раз нужно измерить температуру раствора, чтобы с вероятностью не менее 0,95 можно было утверждать, что средняя арифметическая этих измерений будет отличаться от истинного значения температуры раствора не более чем на 2°С (по абсолютной величине), если среднее квадратическое отклонение измерений не более чем 8°С?
Вариант седьмой
1.Экзаменационный билет содержит два вопроса. Сколько вопросов из общего числа, равного 30, следует подготовить студенту, чтобы с вероятностью 0,8 на экзамене можно было ожидать билет с обоими подготовленными вопросами? 2. Для некоторого предприятия вероятность выхода сотрудника на работу равна 0,9. Найти границы, в которых с вероятностью 0,92 будет находиться число вышедших на работу в наудачу взятый день, если общее число сотрудников предприятия равно 400. 3.Стрелок выстрелил три раза по удаляющейся мишени. Вероятность попадания в нее при первом выстреле равна 0,8, а с каждым следующим выстрелом она уменьшается на 0,1. Составить закон распределения случайной величины X - числа попаданий в цель. Найти математическое ожидание и дисперсию этой случайной величины. 4. Функция распределения непрерывной случайной величины Х имеет вид: F(x)= Найти Р(0,5<Х≤2), М(Х),D(X). 5. Вероятность того, что посетитель магазина купит товар, равна 0,6. Вариант восьмой 1. Определить вероятность того, что номер первой встретившейся автомашины: а) не содержит одинаковых цифр; б) состоит из одинаковых цифр, предполагая, что номера четырехзначные, начиная с номера 0001. 2. Фирма, занимающаяся реализацией оргтехники, рассылает рекламные проекты по организациям. По статистике, примерно в одном случае из десяти при этом следует заказ. Сколько рекламных проспектов следует разослать, чтобы с вероятностью 0,97 можно было ожидать, что доля заказов будет заключена в границах от 0,08 до 0,12? 3. Лампочки елочной гирлянды соединены последовательно. Одна из них перегорела. Составить закон распределения числа проверенных лампочек до обнаружения перегоревшей, если в гирлянде 6 лампочек. Найти дисперсию этой случайной величины. 4. Плотность вероятности продолжительности срока службы некоторого устройства X (лет) имеет вид: φ=(х)= Найти вероятность того, что устройство прослужит не более трех лет, и математическое ожидание М(Х) этой случайной величины. 5. Производительности станков А и В в среднем относятся как 3:1.
Вариант девятый 1. Из коробки, в которой 15 синих и 5 красных стержней для авторучки, наудачу вынимают стержень, фиксируют его цвет и возвращают обратно в коробку. После этого наудачу одновременно извлекают два стержня. Найти вероятность того, что за оба раза извлекли два красных стержня. 2. По статистическим данным, в 20% случаев коммерческому банку удается привлечь имеющиеся у населения сбережения. Найти вероятность того, что среди населения данного округа численностью 1500 человек доля граждан, желающих вложить свои сбережения в коммерческий банк отклонится от указанной вероятности не более чем на 0,03 (по абсолютной величине). 3. В коробке из 10 деталей - 6 окрашенных. Составить закон распределения случайной величины X - числа окрашенных деталей среди трех извлеченных, если после регистрации наличия (или отсутствия) окрашенности очередной извлеченной детали последняя возвращается назад в коробку. Найти математическое ожидание, дисперсию и функцию распределения этой случайной величины. 4. Плотность вероятности случайной величины X имеет вид: φ(х)= Найти вероятность того, что в некотором испытании значение этой случайной величины окажется принадлежащим промежутку (-1; 1) и дисперсию D(X). 5. Вероятность того, что саженец вишни приживется, равна 0,9. Почему нельзя применить неравенство Чебышева для оценки вероятности того, что среди 2000 посаженных саженцев число прижившихся будет заключено в границах от 1850 до 1900? Как нужно изменить левую границу, чтобы применение неравенства Чебышева стало возможным? Решить задачу при соответствующем изменении левой границы. Вариант десятый 1. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность изготовления бракованной детали на первом станке равна 0,02, на втором - 0,03, на третьем - 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего - в два раза меньше, чем второго. Взятая наудачу деталь оказалась бракованной. Найти вероятность того, что она изготовлена на третьем станке. 2. Каждая из пяти упаковок тетрадей содержит две тетради в линейку и три - в клетку. Из каждой упаковки случайным образом отбираются по две тетради. Найти вероятность того, что не менее чем в трех из отобранных пяти пар тетрадей обе тетради будут в клетку. 3. Вероятность того, что договор страховой компании завершится выплатой по страховому случаю, равна 0,1. Страховая компания заключила 2000 договоров. Найти вероятность того, что страховой случай наступит: а) 210 раз; б) от 190 до 250 раз включительно. 4. Законы распределения независимых случайных величин X и Y имеют вид:
Найти вероятность Р(Х=1), Р(У = 2). Составить закон распределения случайной величины Z=X∙У. Проверить выполнение свойства математического ожидания: M(Z) = М(Х) М(У). 5. Функция распределения непрерывной случайной величины X имеет вид:F(x)= Найти математическое ожидание этой случайной величины и вероятность того, что при каждом из трех независимых наблюдений этой случайной величины будет выполнено условие (X < -
Поиск по сайту: |
 R имеет место равенство
R имеет место равенство


 (4)
(4) (5)
(5)
 (5)
(5)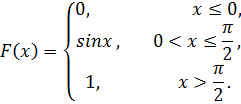







 Тогда
Тогда
 Имеем
Имеем

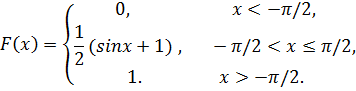
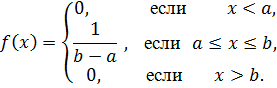



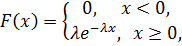
 .
.







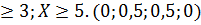
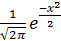
 . Найти вероятность того, что при трех измерениях этой случайной величины в двух случаях ее значения будут принадлежать отрезку [0; 2].
. Найти вероятность того, что при трех измерениях этой случайной величины в двух случаях ее значения будут принадлежать отрезку [0; 2].
 Х
Х  при х Є[0,a]
при х Є[0,a]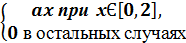
 3,3) = 0,9032. Найти М(Х), D(X), Р(1
3,3) = 0,9032. Найти М(Х), D(X), Р(1 



 ).
).