 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Числові характеристики випадкових величин ⇐ ПредыдущаяСтр 4 из 4
Функція розподілу Для неперервної випадкової величини
де Ми робимо тут припущення, існує наступний інтеграл
Це необхідна і достатня умова існування Для дискретної випадкової величини
де
Моменти мають наступну властивість: якщо існує момент Означені вище моменти мають назву початкових моментів. Серед них найбільш вживаним при описі випадкових величин, особливо в практичних задачах, зокрема, при статистичній обробці сигналів, є момент першого порядку
для неперервної випадкової величини
для дискретної випадкової величини. Математичне сподівання характеризує розташування кривої розподілу (наприклад, щільності
Рис. 2.8. Щільності розподілу імовірностей при різних значеннях математичного сподівання Для розподілу Розглянемо властивості математичного сподівання. 1. Фізична розмірність математичного сподівання співпадає з фізичною розмірністю самої випадкової величини. 2. Нехай
3. Якщо
якщо
4. Якщо
5. Якщо випадкова величина невід’ємна, тобто при всіх 6. Якщо для двох випадкових величин виконується нерівність 7. Математичне сподівання суми (різниці) двох випадкових величин дорівнює сумі (різниці) їх математичних сподівань:
Остання формула може бути узагальнена на
8. Математичне сподівання добутку незалежних випадкових величин
Формула для математичного сподівання добутку двох незалежних величин також може бути узагальнена для
9.Якщо крива щільності розподілу
Рис. 2.9. Симетричні щільності розподілу імовірностей
Якщо Окрім початкових моментів можуть розглядатися і моменти центрованої випадкової величини
Для дискретної випадкової величини
Із означення центральних моментів випливає, що і для неперервних, і для дискретних випадкових величин центральний момент першого порядку завжди дорівнює нулю, тобто Серед центральних моментів різних порядків найбільше застосування знайшов центральний момент другого порядку, який називають дисперсією випадкової величини. Позначимо її літерою
Для дискретної випадкової величини
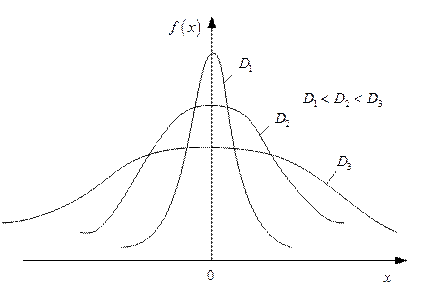
Дисперсія є своєрідною мірою, що характеризує степінь розвіювання значень випадкової величини відносно її математичного сподівання. Чим більша дисперсія випадкової величини, тим більш ймовірними є значні за величиною відхилення значень такої випадкової величини від її математичного сподівання (див. рис. 2.10). Якщо значення випадкової величини є відліками деякого випадкового сигналу, наприклад, напруги на виході антени приймача, то дисперсія зображає собою потужність сигналу. Дисперсія має фізичну розмірність квадрата розмірності випадкової величини. Тому більш зручною характеристикою розвіювання значень випадкової величини
фізична розмірність якого співпадає з розмірністю випадкової величини.
Рис. 2.10. Щільності розподілу випадкових величин з різними дисперсіями
Із означення дисперсії та властивостей математичного сподівання випливає, що
Інколи, при обчисленнях дисперсії, зручніше користуватися саме останнім співвідношенням. Властивості дисперсії: 1. Дисперсія невід’ємна, тобто
2. Дисперсія випадкової величини
3. Для незалежних випадкових величин
Остання властивість може бути розповсюджена на
Причому, в лівій частині останнього співвідношення складові суми можуть бути як зі знаком „+”, так і „−”.
4. Для постійної величини
Для векторної випадкової величини
і центральний змішаний момент
де Величина [1] Тут мова йде про моменти будь-якої, але однієї фіксованої випадкової величини.
Поиск по сайту: |
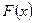 і щільність розподілу імовірностей
і щільність розподілу імовірностей 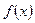 є найбільш повними характеристиками випадкової величини. Але в ряді випадків такий повний опис випадкової величини, особливо на практиці, зробити досить складно або навіть не можливо. Тоді при вивченні випадкових величин обмежуються розглядом менш інформативних характеристик, які являють собою деякі константи (числа) і описують ті чи інші частинні сторони (властивості) функцій та щільностей розподілу імовірностей. Серед цих констант, які застосовуються для отримання загальної кількісної характеристики випадкових величин, особливо важливими є математичне сподівання, дисперсія та моменти різних порядків.
є найбільш повними характеристиками випадкової величини. Але в ряді випадків такий повний опис випадкової величини, особливо на практиці, зробити досить складно або навіть не можливо. Тоді при вивченні випадкових величин обмежуються розглядом менш інформативних характеристик, які являють собою деякі константи (числа) і описують ті чи інші частинні сторони (властивості) функцій та щільностей розподілу імовірностей. Серед цих констант, які застосовуються для отримання загальної кількісної характеристики випадкових величин, особливо важливими є математичне сподівання, дисперсія та моменти різних порядків.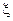 зі щільністю розподілу
зі щільністю розподілу 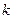 -го порядку визначається за формулою
-го порядку визначається за формулою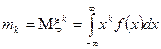 ,
,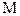 - позначає оператор математичного сподівання.
- позначає оператор математичного сподівання. .
.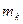 .
.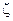 момент
момент 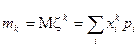 , (2.4)
, (2.4) - імовірність, з якою випадкова величина
- імовірність, з якою випадкова величина 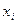 , тобто
, тобто  Додавання в правій частині співвідношення (2.4) виконується по всіх можливих значеннях дискретної випадкової величини
Додавання в правій частині співвідношення (2.4) виконується по всіх можливих значеннях дискретної випадкової величини 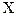 дискретної випадкової величини є зліченна множина, тобто
дискретної випадкової величини є зліченна множина, тобто  , то необхідною і достатньою умовою існування моменту
, то необхідною і достатньою умовою існування моменту 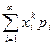 , тобто
, тобто .
. -го порядку, то існують і всі моменти порядку
-го порядку, то існують і всі моменти порядку  ; якщо не існує моменту
; якщо не існує моменту 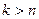
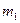 , який носить назву математичного сподівання або середнього випадкової величини. Будемо надалі позначати його літерою
, який носить назву математичного сподівання або середнього випадкової величини. Будемо надалі позначати його літерою 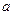 . Тоді
. Тоді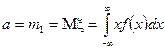


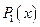 (рис. 2.8, а) математичне сподівання
(рис. 2.8, а) математичне сподівання  , для розподілу
, для розподілу 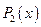 математичне сподівання
математичне сподівання 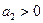 . Випадкова величина, у якої математичне сподівання
. Випадкова величина, у якої математичне сподівання  (рис. 2.8, в), називається центрованою.
(рис. 2.8, в), називається центрованою.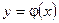 отримана випадкова величина
отримана випадкова величина 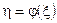 . Тоді, якщо
. Тоді, якщо  - щільність розподілу імовірностей первинної випадкової величини
- щільність розподілу імовірностей первинної випадкової величини 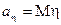 випадкової величини
випадкової величини 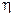 знаходиться за формулою
знаходиться за формулою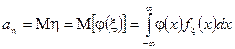 .
.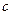 - дійсна або уявна постійна величина, то
- дійсна або уявна постійна величина, то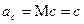 ;
;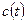 - невипадкова, у загальному випадку, комплексна функція, то
- невипадкова, у загальному випадку, комплексна функція, то .
.
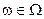
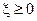 , то і
, то і 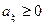 . Аналогічно, коли
. Аналогічно, коли  , то і
, то і  .
.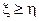 , то і
, то і 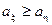 .
. .
.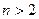 випадкових величин
випадкових величин 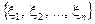 . Наприклад, при
. Наприклад, при 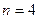 можливе одне із таких співвідношень
можливе одне із таких співвідношень .
.
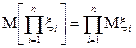 .
.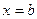 (див. рис. 2.9, а), то
(див. рис. 2.9, а), то  .
.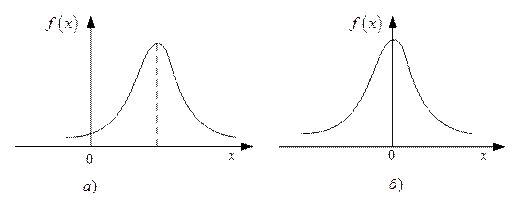
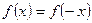 (див. рис. 2.9, б), то
(див. рис. 2.9, б), то 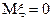 .
. . Такі моменти мають назву центральних. Визначаються вони так. Для неперервної випадкової величини
. Такі моменти мають назву центральних. Визначаються вони так. Для неперервної випадкової величини 

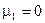 .
. . Тоді для неперервної випадкової величини
. Тоді для неперервної випадкової величини  .
.
 ,
,
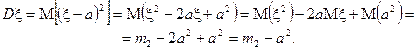
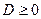 , причому
, причому  лише для невипадкової функції
лише для невипадкової функції 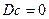 і
і  .
.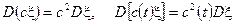 .
.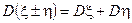 .
.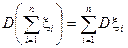 .
. .
.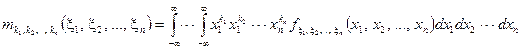
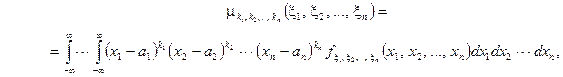
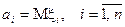 .
.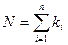 називається порядком змішаного моменту.
називається порядком змішаного моменту.