Мода та медіана випадкової величини

План

1. Математичне сподівання та його властивості.

2. Мода та медіана випадкової величини.

3. Дисперсія та середнє квадратичне відхилення.

4. Початкові та центральні моменти.

5. Асиметрія та ексцес.

Математичне сподівання та його властивості.

Закон розподілу ймовірностей як для дискретних, так і для неперервних випадкових величин дає повну інформацію про них. Проте на практиці немає потреби так докладно описувати ці величини, а достатньо знати лише певні параметри, що характеризують їх істотні ознаки. Ці параметри і називають числовими характеристиками випадкових величин.

Однією з найчастіше застосовуваних на практиці характеристик є математичне сподівання.

Термін «математичне сподівання» випадкової величини Х є синонімом терміна «середнє значення» випадкової величини X.

Математичним сподіванням випадкової величини Х, визначеною на дискретному просторі Ω, називається величина .

Якщо Ω — обмежена множина, то: .

Якщо простір Ω є неперервним, то математичним сподіванням неперервної випадкової величини Х називається величина .

Якщо Ω = (– ¥; ¥), то: .

Якщо Ω = [a; b], то:

Властивості математичного сподівання

1. М (С) = С.

2. М (СХ) = СМ (Х).

3. Якщо А і В є сталими величинами, то .

Приклад. Закон розподілу дискретної випадкової величини задано таблицею:

Обчислити М (Х).

Розв’язання.

Приклад. За заданою щільністю ймовірностей

обчислити М (Х).

Розв’язання.

Мода та медіана випадкової величини.

Модою (Мo) дискретної випадкової величини Х називають те її можливе значення, якому відповідає найбільша ймовірність появи.

Модою для неперервної випадкової величини Х називають те її можливе значення, якому відповідає максимальне значення щільності ймовірності:

f (Mо) = max.

Якщо випадкова величина має одну моду, то такий розподіл ймовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним. Існують і такі розподіли, які не мають моди. Їх називають антимодальними.

Медіаною (Ме) неперервної випадкової величини Х називають те її значення, для якого виконуються рівність ймовірностей подій. Медіану визначають із рівняння:

Приклад. Робітник під час роботи обслуговує три верстати-автомати. Імовірність того, що верстат-автомат потребує уваги робітника за певний проміжок часу, — величина стала і дорівнює 0,8.

Побудувати закон розподілу ймовірностей дискретної випадкової величини Х — числа верстатів, які потребують уваги робітника за певний проміжок часу. Знайти Мо.

Розв’язання.

Можливі значення випадкової величини:

Х = 0, 1, 2, 3.

Імовірності цих можливих значень такі:

p₁ = (0,2)³ = 0,008;

p₂ = 3р q² = 3 × 0,8 × 0,04 = 0,096;

p₃ = 3p²q = 3 × 0,64 × 0,2 = 0,384;

p₄ = p³ = (0,8)³ = 0,512.

Запишемо закон таблицею:

Із таблиці визначаємо Мo = 3.

Отже, дістаємо одномодальний розподіл.

Приклад. За заданою щільністю ймовірностей

Знайти а і F(x), Mo.

Розв’язання.

За умовою нормування маємо:

Щільність ймовірностей зі знайденим а матиме вигляд

Графік f(x):

Згідно з рисунком маємо f (1) = max. Отже, Мo = 1.

Визначаємо Мe:

Отже,

Для визначення Ме застосовуємо рівняння:

3. Дисперсія та середнє квадратичне відхилення.

Математичне сподівання не дає достатньо повної інформації про випадкову величину, оскільки одному й тому самому значенню М (Х) може відповідати безліч випадкових величин.

Приклад. Закони розподілу випадкових величин Х і Y задані таблицями:

Обчислити М (Х) і М (Y).

Розв’язання.

Отже, два закони розподілу мають однакові математичні сподівання, хоча можливі значення для випадкових величин Х і Y істотно різні.

Дисперсією випадкової величини Х називається математичне сподівання квадрата відхилення цієї величини .

Для дискретної випадкової величини Х дисперсія ;

для неперервної .

Якщо Х Î [а; b], то .

Властивості дисперсії

1. .

2. .

3. Якщо А і В — сталі величини, то .

Дисперсію можна обчислити і за такою формулою:

Для дискретної випадкової величини Х: ;

для неперервної: .

Якщо Х Î [а; b], то:

Слід пам’ятати, що дисперсія не може бути від’ємною величиною.

Середнім квадратичним відхиленням випадкової величини Х називають корінь квадратний із дисперсії:

.

Приклад. Закон розподілу дискретної випадкової величини Х задано таблицею:

Обчислити D (X), s (X).

Розв’язання. Маємо:

Приклад. Закон розподілу ймовірностей дискретної випадкової величини Х задано функцією

Обчислити D (X); s (X).

Розв’язання. За заданою функцією розподілу ймовірностей подамо закон розподілу таблицею

Приклад. Задано щільність ймовірностей:

Обчислити D (X); s (X).

Розв’язання.

Поиск по сайту:
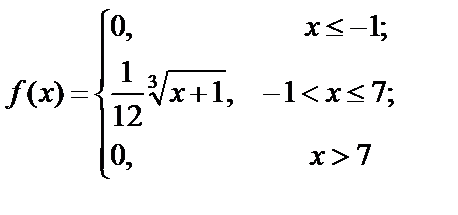
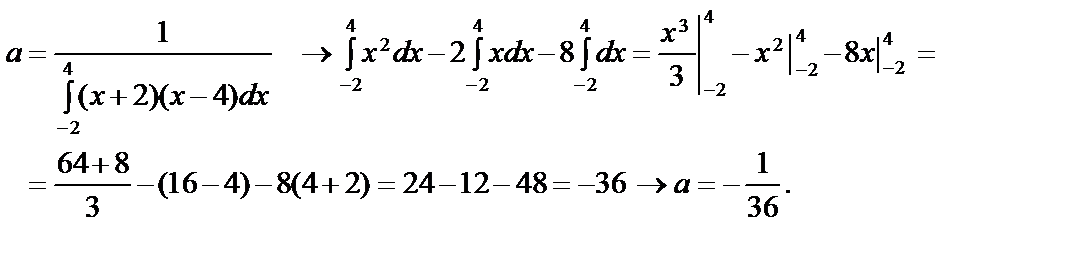
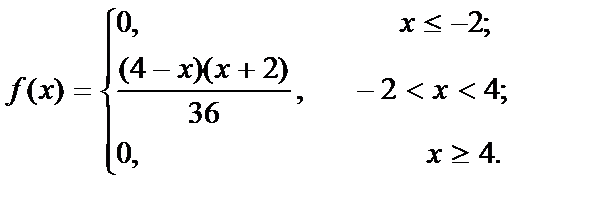
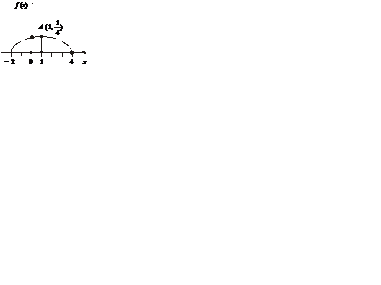
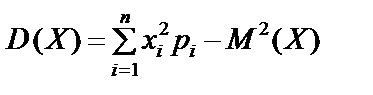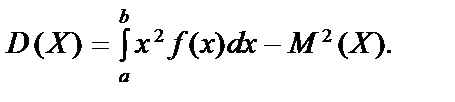