 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Числовые характеристики ДСВ ⇐ ПредыдущаяСтр 2 из 2
Числовые характеристики служат для краткого описания ДСВ и делятся на две группы: характеристики положения и характеристики разброса. К первым относятся математическое ожидание, мода и медиана случайной величины. Дадим их определения: 1) Математическим ожиданием
Математическое ожидание представляет собой средневзвешенное всех значений Х (“весами” служат вероятности отдельных значений) и характеризует порядок величины (десятые, сотые, целые числа, десятки, сотни и т. д.).
Для разобранного в данном разделе примера
2) Модой 3) Медианой Медиана — такое значение случайной величины, для которого функция распределения равна 0. 5. Рассмотрим теперь характеристики разброса. Необходимость их введения можно пояснить на примере. Пусть заданы две случайные величины
По данным из таблицы найдем математическое ожидание
Видно, что при одной и той же величине математического ожидания, отдельные значения 1) Дисперсией
Преобразование этой формулы позволяет привести ее к более удобному виду:
Используя аналогию с Тогда Дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания. Вычислим значение дисперсии для случайной величины Х, рассмотренной в примере. По первой формуле:
По второй формуле:
Следует помнить, что, по своему определению, дисперсия — величина неотрицательная, т. е. 2) Среднеквадратическим отклонением
Характеристика вводится, чтобы иметь возможность указать разброс в той же размерности, что и сама случайная величина (т. к. дисперсия имеет размерность квадрата Х). Для нашего примера Среднеквадратическое отклонение имеет смысл абсолютной погрешности при замене Х ее математическим ожиданием. 3) Вариацией Вариация имеет смысл относительной погрешности.
Поиск по сайту: |
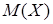 дискретной случайной величины
дискретной случайной величины  называется значение, определяемое следующей формулой:
называется значение, определяемое следующей формулой: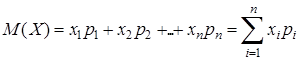 .
.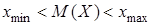 .
.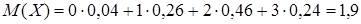 .
. случайной величины называется ее значение, имеющее наибольшую вероятность. В нашем примере
случайной величины называется ее значение, имеющее наибольшую вероятность. В нашем примере 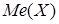 случайной величины называется такое ее значение, для которого выполняется следующее условие:
случайной величины называется такое ее значение, для которого выполняется следующее условие:  .
. .
.


 ,
, .
. отличаются от
отличаются от 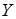 от
от  . Числовые характеристики, определения которых сейчас будут даны, учитывают эту разницу в поведении случайных величин.
. Числовые характеристики, определения которых сейчас будут даны, учитывают эту разницу в поведении случайных величин. случайной величины Х называется математическое ожидание квадрата отклонения Х от своего математического ожидания. Для ДСВ дисперсия вычисляется по формуле:
случайной величины Х называется математическое ожидание квадрата отклонения Х от своего математического ожидания. Для ДСВ дисперсия вычисляется по формуле: .
.

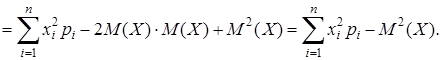
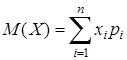 можно обозначить
можно обозначить  .
. .
.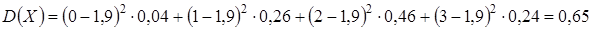 .
. .
. .
. случайной величины Х называется корень квадратный из дисперсии:
случайной величины Х называется корень квадратный из дисперсии: .
. случайной величины Х называется отношение
случайной величины Х называется отношение 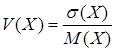 .
.