Экспоненциальное распределение

Экспоненциальное распределение — это непрерывное распределение с сильной асимметрией (рис. 7.5.4). В левой части кривая распределения при приближении к 0 уходит вертикально вверх, а в правой части постепенно понижается.

Ниже описаны случаи, к которым применимо экспоненциальное распределение. Если события происходят случайно, независимо и с постоянной частотой, время ожидания между двумя последовательно наступающими событиями имеет экспоненциальное распределение. (Обратите внимание на то, что при этом общее количество событий подчиняется распределению Пуассона).

Вот несколько примеров случайных величин, которые могут иметь экспоненциальное распределение.

1. Промежутки времени между появлением посетителей в авторемонтной мастерской.

2. Периоды времени нормальной работы копировального аппарата между появ- лениями неисправностей, требующих вмешательства специалиста по ремонту.

3. Длительность типичного телефонного разговора.

4. Время до выхода из строя кинескопа телевизора.

5. Затраты времени на обслуживание одного покупателя.

Экспоненциальное распределение не обладает памятью в том несколько удивительном смысле, что если вы ожидаете события в течение некоторого промежутка времени и это событие не наступило, то в результате среднее время ожидания этого события не уменьшилось по сравнению с тем, что было в момент начала ожидания. Этот факт становится понятным, если мы вспомним, что события наступают независимо друг от друга и каждое такое событие “не знает” о том, что в последнее время предыдущее событие не происходило.

Что можно сказать, исходя из изложенного выше, о телефонных разговорах? Представьте себе, что вы руководите автоматической телефонной станцией, через которую осуществляются соединения средней длительностью пять минут. Рассмотрим все телефонные переговоры, которые начались в настоящий момент. Вы ожидаете, что эти разговоры будут продолжаться в среднем в течение пяти минут, причем длительность отдельных разговоров имеет экспоненциальное рас­пределение. По истечении одной минуты некоторые разговоры оканчиваются. Однако для всех остальных разговоров ожидается продолжение в среднем также в течение следующих пяти минут. Это связано с тем, что самые короткие звонки уже удалены из рассмотрения. В такое, возможно, трудно поверить, однако это подтверждается (приблизительно) реальными данными.

Ниже описаны основные свойства экспоненциального распределения. Обратите внимание на то, что для этого распределения нет «нормального приближения»”, поскольку экспоненциальное распределение всегда очень асимметрично.

Для экспоненциального распределения:

1. Стандартное отклонение всегда равно среднему значению σ = µ.

2. Вероятность того, что имеющая экспоненциальное распределение случайная величина X со средним значением µ принимает значение, меньшее а, выражается формулой

Р(Х< а) = 1 -

Если события происходят независимо друг от друга и с постоянной частотой, между экспоненциальным распределением и распределением Пуассона существует определенная взаимосвязь. Количество событий для любого фиксированного промежутка времени имеет распределение Пуассона, а время ожидания между событиями — экспоненциальное распределение. Этот факт проиллюстрирован на рис. 7.5.5. Распределение времени ожидания от некоторого фиксированного момента времени до наступления события подчиняется экспоненциальному закону.

Пример. Визиты клиентов

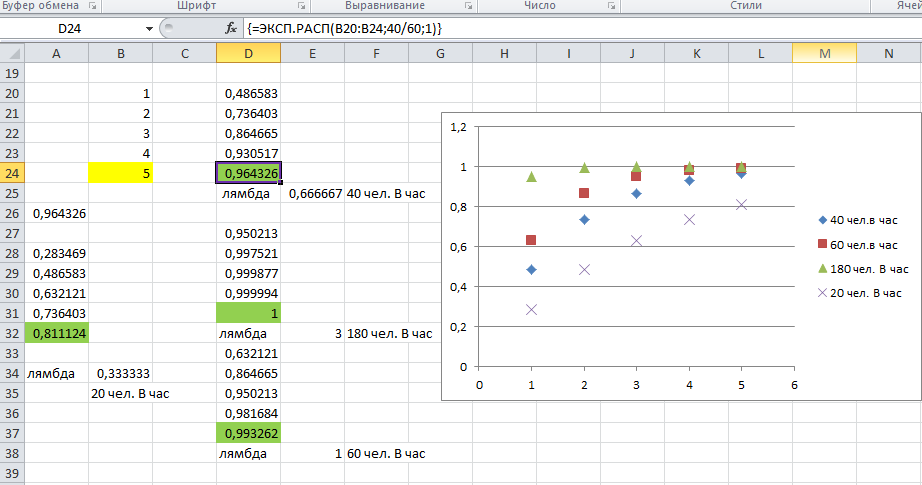
Предположим, что клиенты приходят независимо друг от друга с постоянной средней частотой 40 посетителей в час. Чтобы найти вероятность того, что в течение следующих пяти минут придет по меньшей мере один клиент, необходимо вычислить вероятность того, что подчиняющееся экспоненциальному распределению время ожидания следующего клиента будет меньше пяти минут. Поскольку в течение каждого часа в среднем приходят 40 клиентов, среднее значение интересующей нас экспоненциально распределенной случайной величины составляет 1/40 = 0,025, часа или 0,025 * 60= 1,5 минуты. Таким образом, искомая вероятность равна P(X<5)=1-e^-5/1,5 = 0,96 . Это значение можно также вычислить с помощью Excel, воспользовавшись формулой 1-ЕХР (-5/1, 5). Таким образом, вероятность появления в течение следующих пяти минут по меньшей мере одного клиента оказывается довольно высокой (96%).

Поиск по сайту: