 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 7. Інтегральне числення
1. Первісна функція та невизначений інтеграл. 2. Визначений інтеграл. 3. Використання поняття визначеного інтегралу в економіці.
7.1. Первісна функція та невизначений інтеграл
Задачею диференціального числення було знаходження похідної від заданої функції y=f(x). Задача інтегрального числення протилежна: потрібно визначити функцію, похідна від якої відома. Означення. Функція F(x) називається первісною для функції f(x), якщо f¢(x)=F(x). Приклад. Для функції y=3x2 первісними є функції F(x)=x3; F(x)=x3+5; F(x)=x3-6,3 тощо. Означення. Невизначеним інтегралом від функції f(x) називається сукупність усіх первісних цієї функції. Використовується позначення
де f(x)dx - підінтегральний вираз, а C - стала інтегрування. З геометричного погляду невизначений інтеграл – це сукупність (сім’я) ліній F(x)+C (рис. 7.1).
y=x3+2 (C=2)
x
Наведемо таблицю основних інтегралів. Доведення кожної рівності полягає у її диференціюванні.
Приклади. 1) 2) 3) Із означення невизначеного інтеграла випливають такі властивості інтегрування: 1) 2) 3) 4)
Приклади. 1. Знайти Тоді dx=4dt, отже,
2. Знайти
3. Знайти
4. Знайти 5. Знайти
Інтегрування частинами потребує певних навиків. Розглянемо цей спосіб на прикладах. Приклади. 1. Знайти інтеграл
Отже,
2. Знайти
Для інтегрування раціональних дробів, тригонометричних виразів тощо, використовуєть спеціальні прийоми. Розглянемо два приклади відшукання невизначених інтегралів від раціональних дробів. Приклади. 1) 2)
В економіці часто застосовують такі функції, як y=lnx та y=1-e-x. Інтеграли від цих функцій :
(перевірка виконується диференціюванням). Зазначимо, що не всі інтеграли можна виразити через елементарні функції. Так, наприклад, інтеграли
7. 2. Визначений інтеграл Розглянемо неперервну функцію f(x) на відрізку [a,b]. Розіб’ємо цей відрізок на n частин: x0=a, x1=a+h,…, xi=a+ih,…,xn=a+nh=b, де Означення. Сума
визначеним інтегралом від функції f(x) на відрізку [a,b] і позначається через Геометричний сенс визначеного інтеграла. Нехай функція f(x) для всіх значень аргументу xÎ[a,b] є додатною. Тоді інтегральна сума представляє собою сумарну площу прямокутників S1,…,Si,…,Sn (рис. 7.2). Визначений інтеграл у цьому випадку дорівнює площі криволінійної трапеції, обмеженої кривими y=0, x=a, x=b та y=f(x).
S1 S2 ……Sn.
0 a x1 x2 ..xn-1 b x Рис. 7.2. Теорема. Визначений інтеграл від функції f(x) на відрізку [a,b] дорівнює приросту первісної на цьому відрізку:
Останню формулу називають формулою Ньютона-Лейбніца. Зазначимо, що в деяких підручниках визначеним інтегралом від функції f(x) на відрізку [a,b] називать приріст первісної F(b)-F(a) на цьому відрізку. Виходячи з такого означення доводяться теорему про те, що визначений інтеграл дорівнює границі інтегральних сум. Приклади. 1) 2) 3)
4) знайти площу фігури, обмежену графіком функції
1 9 x Рис. 7.3. Невласні інтеграли. На практиці трапляються визначені інтеграли, задані на нескінченному інтервалі (та визначені інтеграли від необмеженої функції). Такі інтеграли називають невласними. Невласний інтеграл обчислюється за допомогою границі. Приклади. 1.
Рис. 7.4. 2) Інтеграл від необмеженої функції (рис. 7.5):
a 4 x Рис. 7.5.
7.3 . Використання поняття визначеного інтегралу в економіці
7.3.1. Визначення загального обсягу випущеної продукції Нехай деяка фірма випускає один вид продукції, використовуючи один ресурс. Виробнича функція фірми має вигляд q=q(x), де x - затрати ресурсу, а q - обсяг випуску. Затрати ресурсу x є функцією від часу t, наприклад, x=x(t). Тоді загальний обсяг продукції Q за час від T0 до T1 обчислюється за допомогою визначеного інтегралу
При
7.3.2. Визначення коефіцієнта Джинні Нехай y=y(x) - частка (доля) приватного капіталу деякої країни, яка перебуває у власності групи людей, що становлять частку (долю) x населення цієї країни. Наприклад, у тому випадку, коли 30% населення володіє 10% капіталу, 60% населеня 35% капіталу, і 85% 60% капіталу, маємо таке: y(0,3)=0,1; y(0,6)=0,35; y(0,85)=0,6. Очевидно, що завжди y(0)=0 та y(1)=1.
y
0,3 0,85 1 Рис. 7.6.
Очевидно, що у разі абсолютно рівномірного розподілу багатства в країні крива Лоренца є бісектрисою прямого кута (прямою y = x). Зі збільшенням нерівності збільшується площа між кривою y=y(x) та прямою y = x. Числове значення цієї площі K (0<K<1/2) називають коефіцієнтом Джинні. Приклад. Крива Лоренца деякої країни має вигляд Із визначення коефіцієнта Джинні випливає, що для кривої Лоренца
Для кривої Лоренца y=x2 маємо такий коефіцієнт Джинні:
7.3.3. Обчислення дисконтованого значення грошових потоків Як відомо з теми 3, теперішню вартість майбутніх грошей обчислюють за формулою
де r - ставка відсотка. Останню формулу для невеликих значень можна записати у вигляді
оскільки ln(1+r)»r (справді, ln1,03=0,0296; ln1,05=0,0488; ln1,08=0,077 ) Нехай деяка фірма здійснює потік інвестицій FV1, FV2,…, FVn в моменти часу t1, t2,…,tn=T. Тоді дисконтована (чиста) теперішня вартість NPV потоку інвестицій представляє собою суму
У тому випадку, коли окремі інвестиції роблять невеликими порціями досить часто (всі Di =ti-ti-1 -малі, де t0=0; i=1,…,n), NPV можна вважати інтегральною сумою, яка в неперервному випадку ( n®¥; всі Di®0; послідовність значень FV1=FV(t1), FV2=FV(t2),…, FVn=FV(T) описує деяка функція FV(t), 0£t£T ) перетворюється в інтеграл
Приклад. Нехай потік інвестицій задає функція FV(t)=100-10t . Ставка відсотка r=10% (r=0,1). Довжина періоду інвестування T=5 (років). Визначити дисконтовану теперішню вартість потоку (рис.7.7,б):
Для порівняння визначимо недисконтовану вартість цього потоку (рис 7.7,а):
(5;30,3)
а б Рис.7.7. 7.3.4. Розрахунок надлишку виробника та надлишку споживача З курсу мікроекономіки відомо, що в умовах досконалої конкуренції ринкова (рівноважна) ціна на кожен товар відповідає точці перетину кривої попиту D=D(Q) та кривої пропозиції S=S(Q) (рис. 7.8). Кожна точка (P;Q) на кривій попиту визначає кількість товару Q, який був би проданий за ціни P. Незважаючи на те, що на ринку весь товар реально продають за ціною P*, деяка i-та (i=1,…,n) частина споживачів згідна була б купити свою частку товару DQ*i, заплативши і дещо вищу ціну Pi>P* (щоправда, за ціни Pi всього буде продано тільки Qi одиниць товару). Отже, кожна i-та частина споживачів завдяки ринковому механізмові виграє в ціні на (Pi-P*)DQ*i . Вважаючи, що за деякої досить високої ціни P0² товар не купуватимуть взагалі, маємо такий загальний виграш (надлишок) усіх споживачів:
де i=1 відповідає ціні P0² , а i=n ‑ ціні P*. Очевидно, що в неперервному випадку надлишок (виграш) споживачів дорівнює площі S1 фігури P0²E P* (рис.7.8). Кожна точка (Q;P) на кривій пропозиції визначає кількість товару Q, яка була б продана на ринку за ціни P. Оскільки деяка j–та (j=1,…,m) частина виробників згідна виробляти та постачати на ринок частку товару DQj і за ціни Pj<P* (однак не нижчою від P¢0), то завдяки ринковому механізму (який визначив ціну P*) загальний надлишок (виграш) усіхвиробників дорівнює (де j=1 відповідає ціні P0¢ , а j=m ‑ ціні P*)
тобто площі S2 фігури P*EP¢0 (див. рис. 7.8).
Q0 Qi DQi Q*
Рис. 7.8. Приклад. В умовах досконалої конкуренції крива попиту має вигляд D(Q)=(Q-10)2+200, а крива пропозиції – S(Q)=Q2+100. Знайти загальний надлишок споживача та загальний надлишок виробника, якщо максимальна ціна споживача – 225 одиниць, а виробника – 125 одиниць. Точку рівноваги знаходимо з рівняння D(Q)= S(Q); (Q-10)2+200=Q2+100; Q*=10; P*=200. Цінам P0²=225 та P0¢=125 відповідає мінімальна кількість товару в обсязі Q0=5. Надлишок (виграш) споживача дорівнює площі фігури S1, тобто його обчисдюють за допомогою визначеного інтеграла
Надлишок (виграш) виробника дорівнює площі фігури S2, тобто знаходиться зи допомогою визначеного інтеграла
7.3.5. Дослідження функцій густини розподілу ймовірностей У курсі “Теорія ймовірності і математична статистика” буде з’ясовано, що ймовірність потрапляння неперервної випадкової величини x в інтервал [a;b] дорівнює інтегралу Знайдемо невласні інтеграли від деяких таких функцій. 1. Диференціальна функція (густина) рівномірного розподілу ймовірностей (рис. 7.9,а)
2. Диференціальна функція (густина) показникового розподілу ймовірностей (рис. 7.9,б) f(x)=kxe-kx
3. Диференціальна функція (густина) нормального закону (закону Гауса) розподілу (рис. 7.9,в) За допомогою спеціальних методів можна показати, що
а б в Рис. 7.9. Ці інтеграли широко застосовуються в курсі “Економетрія”.
1. Поняття про диференціальні рівняння. Рівняння з розділеними змінними. 2. Лінійні диференціальні рівняння. 3. Задача Коші. Застосування диференціальних рівнянь в економіці.
8.1. Поняття про диференціальні рівняння. Рівняння з розділеними змінними
Ряд задач економіки та упраління, що розгортаються в часі, описуються диференціальними рівняннями. Означення. Звичайним диференціальним рівнянням називається рівняння, у яке входять незалежна змінна, функція від цієї змінної та похідні різних порядків: F(x,y,y¢,y²,…)=0 Найвищий порядок похідної при цьому називається порядком рівняння. Приклади. 1. Диференціальне рівняння другого порядку y²+2y¢-3y=x2+1 . 2. Диференціальне рівняння третього порядку y¢²=cos(x). Означення. Розв’язком диференціального рівняння називають функцію, яка в разі підстановки у рівняння перетворює його у тотожність. Приклади. 1. Розв’язками диференціального рівняня першого порядку y¢=3x2 є функції y=x3, y=x3+10, y=x3-3.5,… Отже, загальний розв’язок цього рівняння має вигляд y=x3+C , де C - довільна стала. 2. Загальним розв’язком рівняння другого порядку y²=sin(x) є сім’я функцій (кривих) y= -sin(x)+C1x+C2, де C1 та C2 - довільні сталі. Частковими ж розв’язками є, наприклад, функції y= -sin(x)+10, y= ‑ sin(x)+2x+1 тощо. Крім звичайних диференціальних рівнянь, розглядають також рівняння з частинними похідними (шукана функція залежить від декількох змінних), наприклад: u²x(x,y)+u¢y(x,y)=2u(x,y)+x+y Означення. Звичайним диференціальним рівнянням першого порядку називається рівняння, у яке входить змінна x, функція y та перша похідна y¢(x): F(x,y,y¢)=0 (8.1) Розглянемо деякі способи розв’язування таких рівнянь. Означення. Диференціальне рівняння вигляду f1(x)×j2(y)dx+f2(x)×j1(y)dy=0 (8.2) називається рівнянням з розділеними змінними. Приклади. 1. Розв’язати диференціальне рівняння Виконуємо ділення на вираз
Почленно інтегруємо:
застосовуючи послідовно заміни 1-x2=t (звідки -2xdx=dt; xdx=(-dt)/2) та
Отримано загальний розв’язок (загальний інтеграл) диференціального рівняння, який є неявною функцією. 2. Розв’язати диференціальне рівняння y¢=7x+y . Розділяємо змінні:
Інтегруємо праву та ліву частини:
Позначивши сталу lnC (тобто, сталу, яка може набувати довільних значеннь) через C (ця нова константа також може приймати довільні значення), матимемо: -7y=7x+C . Отже, загальним розв’язком диференціального рівняння є неявна функція (що залажить від сталої C) 7y+7x=C . 3. Розв’язати диференціальне рівняння
arctgy=arctgx+C . Отримано загальний розв’язок у неявому вигляді. Перейдемо до розв’язку у вигляді явної функції. Враховуючи той факт, що як стала C, так і стала arctgC , може набувати довільних значень, отримуємо: arctgy=arctgx+arctgC. Знайшовши тангенс від суми аргументів, одержуємо:
(загальний розв’язок, записаний у явному вигляді).
8.2. Лінійні диференціальні рівняння
Означення. Лінійне однорідне диференціальне рівняння першого порядку має вигляд y¢=a(x)×y=0 (8.3) Таке рівняння розв’язують як рівняння із розділеними змінними:
Означення. Лінійне диференціальне рівняння першого порядку має вигляд y¢+a(x)×y=b(x) (8.4) Одним із методів його розв’язування є шукання розв’язку у вигляді
Приклад. Розв’язати лінійне (неоднорідне) рівняння
Розв’язок однорідного рівняння y¢+2xy=0 має вигляд
Розв’язок неоднорідного рівняння шукаємо у вигляді
де C(x) функція від x . Знайдемо похідну від цього виразу: і підставимо відшукані значення y та y¢ в початкове рівняння:
С¢(x)=2x ; dC(x)=2xdx ; C(x)=x2+C . Отримуємо загальний розв’язок
Приклад. Розв’язати лінійне рівняння першого порядку 2xy¢-y=3x2.
Загальним розв’язком однорідного рівняння
Знаходимо загальний розв’язок початкового рівняння у вигляді Підставляючи y та y¢ в рівняння, маємо
Отже, загальний розв’язок неоднорідного рівняння є таким:
Означення. Лінійне однорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами – це рівняння вигляду y² + py¢ + qy=0 , (8.5) де p та q - сталі величини. З метою розв’язування таких рівнянь будують характеристичне рівняння l2+pl+q=0 Доведено, що у тому випадку, коли характеристичне рівняння має два різні дійсні корені l1 та l2 , загальний розв’язок диференціального рівняння такий:
де C1 та C2 - довільні сталі. У випадку кратних дійсних коренів l1=l2=l характеристичного рівняння загальний розв’язок диференціального рівняння має вигляд
Приклад. Розв’язати рівняння y²+2y¢-15y=0. Будуємо характеристичне рівняння l2+2l-15=0, звідки l1=3; l2=-5. Отже, загальний розв’язок є такий: Приклад. Розв’язати рівняння y²+2y¢+y=0. Будуємо характеристичне рівняння l2+2l+1=0, звідки l1=l2=-1. Отже, загальний розв’язок:: 8.3. Задача Коші. Застосування диференціальних рівнянь в економіці
Задачею Коші називається задача знаходження часткового розв’язку диференціального рівняння. Для рівнянь першого порядку задача полягає у знаходженні такої функції, яка - задовольняє рівнянню F(x,y,y¢)=0; - проходить через точку (x0;y0). Приклад. Розв’язати задачу Коші
Знаходимо загальний розв’язок диференціального рівняння з розділеними змінними:
arctgy=lnx+lnC ; y=tg(ln(Cx)) . На основі початкової умови y(1)=0 визначаємо конкретне значення константи C: 0=tg(ln(C×1)) ; C=1 . Таким чином, розв’язком задачі Коші є функція y=tg(lnx). Приклад. Розв’язати задачу Коші
Знаходимо загальний розв’язок:
lnx=(-1/2)ln(1+y2) + lnC;
x2×(1+y2)=C. Визначаємо сталу C, виходячи з початкових умов: Розв’язок задачі Коші, отже, такий: x2(1+y2)=5.
Ріст при постійному темпі приросту. Нехай в початковий момент часу t0=0 кількість населеня деякої країни становить P0. Нехай темп приросту кількості цього населення є сталим (зазначимо, що приріст може бути як додатнім, так і від’ємним) і дорівнює величині T. Нагадавши, що темп приросту функції y=y(t) обчислюється за формулою
Розділяємо змінні і знаходимо загальний розв’язок:
lny=T×t+lnC ; y=C×eT×t . Оскільки при t=0 величина y(0)=P0 , то P0=CeT×0 =C і далі y(t)=P0 eT×t (розв’язок задачі Коші). Знайдена функція y(t)=P0×eT×t дозволяє прогнозувати кількість населення в довільний момент часу. Наприклад, при річному темпі приросту T = -2% (темпі спаду в розмірі 2%) через t=25 (років) кількість населення становитиме P0× e-0,02×25 = P0× e-0,5 »0,607P0. Зазначимо, що ця ж функція y(t)=P0×eT×t описує динаміку росту цін при постійному темпі інфляції. Ріст при спадному темпі приросту. Нехай деяка фірма починає випускати на продаж новий товар. Нехай на момент часу t0=0 на ринку вдалося продати y(t0)=y(0)=y0 одиниць товару. Позначимо через y(t) кількість проданого товару в довільний момент часу t і поставимо задачу визначення (прогнозування) цієї величини y(t). В теорії маркетингу досліджено, що темп приросту Ty кількості проданого товару лінійно спадає в залежності від обсягу y продажу цього товару. Нехай темп приросту (спаду) Ty залежно від величини y є такою лінійною функцією: Ty = b-ay. Отже, для для знаходження функції y=y(t) потрібно розв’язати задачу Коші:
Розв’язуємо дифренціальне рівняння
дробів
При конкретному значенні y(0)=y0 отримуємо конкретну криву (функцію) вигляду
y0=Cb/(1+Ca)
Рис. 8.1.
Попит при постійній еластичності. Нехай Q - розмір попиту на деякий товар залежно від його ціни p. Нехай Q(p0)=Q0 . Нехай еластичність попиту за ціною EQp=E є сталою на деякому інтервалі. Для побудови функції попиту Q=Q(p) зі сталою еластичністю розв’язуємо задачу Коші (оскільки еластичність EQp обчислюються за допомогою похідної: EQp=Q¢×(p/Q) ):
Q=C×pE . З урахуванням початкових умов отримуємо явний вигляд функції попиту
Зокрема, при еластичності E = -1 (збільшення ціни на 1% приводить до зменшення попиту на 1%) попит залежно від ціни описує функція
Корисність при постійній схильності до ризику. Схильність особи до ризику (дисципліна “Економічний ризик”) r(x) залежно від кількості багатства xобчислюють за формулою Потрібно розв’язати диференціальне рівняння r(x)= Маємо задачу Коші
тобто лінійне однорідне рівняння другого порядку U²-rU¢=0. Будуємо характеристичне рівняння l2-rl=0, коренями якого є числа l1 = 0 та l2 = r. Отримуємо загальний розв’язок: U(x)=C1e0×x+C2er×x =C1+C2 er×x . Враховуючи першу початкову умову U(0)=0, маємо C1= -C2, отже U(x)=C-C erx . Друга початкова умова U¢(0)=k дає - C×r×er×0 =k, звідки C=(-k)/r . Отже, функція корисності клієнта має вигляд Зокрема, при r = -0,2 та k=1
U(x)
Рис. 8.2.
Отже, у разі сталої схильності до ризику r = -0,2 (незалежно від кількості багатства x) функція корисності клієнта має вигляд U(x)=5-5e-0,2x (рис. 8.2).
1. Числові ряди. 2. Степеневі ряди.
9.1 . Числові ряди У деяких задачах розглядають суми, що складаються із нескінченної кількості доданків. Властивості таких нескінченних сум часто суттєво відрізняються від властивостей сум скінченної кількості доданків. Наприклад, для суми S=1-1+1-1+1-1+… згідно з асоціативним законом маємо S=(1-1)+(1-1)+… та S=1-(1-1)-(1-1)-… . Отже, для нескінченних сум асоціативний (сполучний) закон додавання не виконується. Означення. Нехай задано нескінчену послідовність {an}=a1,a2,…,an,… . Тоді вираз a1+a2+…+an+…= Розглянемо часткові суми числового ряду: S1=a1 ; S2=a1+a2 ; ………….. Sn=a1+a2+…+an ; ……………. Означення. Ряд називається збіжним, якщо послідовність його часткових (частинних) сум має скінченну границю. Ця границя називається сумою ряду
Приклади. 1. Ряд 2. Ряд 3. Нехай у деякій закритій економіці частка національного продукту, яку витрачають на споживання, становить b, а частка, яку вкладають в інвестування 1-b . Нехай початкові інвестиції дорівнюють I. Тоді згідно з теорією Кейнса споживання спричинить нові інвестиції у розмірі b×I . На наступному етапі матимемо інвестиції в розмірі b2×I і так далі. В перспективі національний доход становитиме Y=I+bI+b2I+…=
Властивості збіжних рядів Теорема 1 (необхідна умова збіжності рядів). Якщо ряд Теорема 2. Якщо ряд Крім того, збіжні ряди можна почленно додавати та множити на число.
Достатні ознаки збіжності рядів Теорема 3. Нехай задано два ряди з додатними членами (знакододатні, знакосталі ряди) Теорема 4 (ознака Д’Аламбера). Нехай для ряду з додатними членами
Приклад. Дослідити на збіжність ряд Знаходимо границю
Теорема 5 (ознака Лейбніца). Нехай задано знакозмінний ряд Приклад. Ряд Для обчислення цього ряду, наприклад, з точністю до 0.01 потрібно, щоб
Абсолютна збіжність рядів Означення. Ряд Приклади. 1. Ряд 2. Ряд
9.2. Степеневі ряди Означення. Степеневим рядом називається ряд вигляду c0+c1x+c2x2+…+cnxn+… Приклади. 1. Степеневий ряд 1+x+x2+…+xn+… Тут усі cn=1. 2. Степеневий ряд 1-2x+3x2-4x3+5x4-… Тут cn = (-1)n×(n+1). Очевидно, що за одних значень змінної x ряд може збігатися, а за інших – розбігатися. Тому ставлять задачу звідшукання радіуса збіжності степеневого ряду (тобто такого додатного числа R, що для всіх значень |x|<R степеневий ряд є збіжним). Приклад. 1. Знайти область збіжності степеневого ряду
Згідно з ознакою Д’Аламбера Очевидно, що при –2<x<2 Теорема (без доведення). Степеневий ряд в області його збіжності можна почленно диференціювати та інтегрувати.
Одним із найважливіших результатів математичного аналізу є розклад функцій у ряди. Теорема. Нехай у деякому околі точки x0 функція f(x) є (n+1) разів диференційовною. Тоді в цьому околі функція f(x) розкладається в такий ряд
Цю формулу називають формулою Тейлора. Очевидно, що коли (n+1)–а похідна f(n+1)(x) обмежена, то залишковий член ряду прямує до нуля при x®x0. Отже,
При x0=0 формула Тейлора перетворюється у формулу Маклорена
Легко бачити, що формула Маклорена є степеневим рядом. Таким чином елементарні (шкільні) функції, всі які є багато разів диференційовними, можна розкладасти в степеневі ряди. Приклади. 1. Розкласти в степеневий ряд функцію f(x)=ex. Маємо f(x)=f¢(x) =f²(x) =…=f(n)(x) =…=ex . Далі f(0)=f¢(0)=f²(0)=… …=f(n)(0) =…=e0=1. Отже,
2. Згідно з ознакою Лейбніца ( 2. Оскільки (
Поиск по сайту: |
 ,
,
 y y=x3+5,2 (C=5,2)
y y=x3+5,2 (C=5,2) y=x3-3 (C= -3)
y=x3-3 (C= -3)
 Рис.7.1.
Рис.7.1. (n¹-1) , у тому числі
(n¹-1) , у тому числі ;
; ;
; ;
; ;
; , у тому числі
, у тому числі  ;
; ;
; ;
; ;
; ;
; , у тому числі
, у тому числі  ;
; , у тому числі
, у тому числі  ;
; .
. . Справді,
. Справді,  ;
; ;
; .
. ;
; ;
; (метод заміни змінних, метод підстановки);
(метод заміни змінних, метод підстановки); (інтегрування частинами).
(інтегрування частинами). . Виконуємо заміну (підстановку) x/4=t.
. Виконуємо заміну (підстановку) x/4=t.
 . Виконуємо заміну 2x=t, звідки 2dx=dt. Тепер
. Виконуємо заміну 2x=t, звідки 2dx=dt. Тепер
 . При заміні x=t3-1 маємо x+1=t3 , dx=3t2dt і далі
. При заміні x=t3-1 маємо x+1=t3 , dx=3t2dt і далі
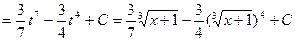
 (заміна 4x=t).
(заміна 4x=t). (заміна 6x-5=t).
(заміна 6x-5=t). . Позначимо вираз lnx через u, а вираз x3dx через dv. Знаходимо du та v:
. Позначимо вираз lnx через u, а вираз x3dx через dv. Знаходимо du та v:
 .
. . Позначимо u=x, dv=e2xdx. Звідси du=dx, v=(1/2)×e2x. Тоді
. Позначимо u=x, dv=e2xdx. Звідси du=dx, v=(1/2)×e2x. Тоді .
. ;
;


 .
. ;
;
 та
та  існують, проте через елементарні функції не виражаються.
існують, проте через елементарні функції не виражаються. .
. називається інтегральною сумою, а границя
називається інтегральною сумою, а границя (7.1)
(7.1) .
. y
y 







 y=f(x)
y=f(x) (7.2)
(7.2) ;
; ;
; (заміна x+1=t)
(заміна x+1=t) ;
; , віссю абсцис та прямими x=1 , x=9 (рис. 7.3).
, віссю абсцис та прямими x=1 , x=9 (рис. 7.3). .
.
 y
y
 Інтеграл, заданий на нескінченному інтервалі (рис. 7.4):
Інтеграл, заданий на нескінченному інтервалі (рис. 7.4):
 ;
;
 y
y


 1 a x
1 a x
 .
.
 y
y



 .
. , x(t)=100e0,2t, T0=0 та T1=5 (років) загальний обсяг випущеної за п’ять років продукції
, x(t)=100e0,2t, T0=0 та T1=5 (років) загальний обсяг випущеної за п’ять років продукції
 На рис. 7.6 зображена відповідна крива (крива Лоренца).
На рис. 7.6 зображена відповідна крива (крива Лоренца).

 0,6
0,6

 0,1
0,1 x
x .Знайти коефіцієнт Джинні цієї країни.
.Знайти коефіцієнт Джинні цієї країни.
 .
. ,
, ,
,
 .
.


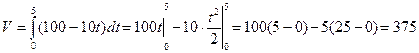 .
.


 100 100
100 100
 (5;50)
(5;50)
 ,
, ,
,
 P(ціна)
P(ціна)



 P²0 S(Пропозиція)
P²0 S(Пропозиція)


 Pi S1
Pi S1
 P* S2 E D(Попит)
P* S2 E D(Попит) P¢0
P¢0

 Q(Кількість)
Q(Кількість)

 .
.

 .
. , де f(x) - диференціальна функція (функція густини) розподілу ймовірностей величини x.
, де f(x) - диференціальна функція (функція густини) розподілу ймовірностей величини x. дорівнює
дорівнює .
.
 .
. .
. ;
; ;
;  .
.


 1/(b-a)
1/(b-a)


 .
. , розділивши тим самим змінні:
, розділивши тим самим змінні:
 ,
, ;
; ;
; ;
; ;
; .
. ;
;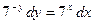 .
. .
. ;
; ;
; .
. ;
; ;
;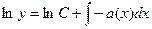 ;
; ;
; - загальний розв’язок.
- загальний розв’язок. .
. .
. .
. ,
, ,
,

 ;
; .
.
 є сім’я функцій (або, іншими словами, функція, яка залежить від сталої C)
є сім’я функцій (або, іншими словами, функція, яка залежить від сталої C) .
. . Тоді
. Тоді  .
.

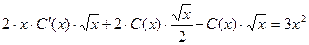
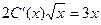




 .
. ,
,

 .
. .
. ;
; .
. (заміна y2=t Þ 2ydy=dt Þ ydy=dt/2);
(заміна y2=t Þ 2ydy=dt Þ ydy=dt/2); ;
; ;
; , приходимо до такої задачі Коші:
, приходимо до такої задачі Коші:
 ;
; .
. ;
; (дріб
(дріб  розкладено на суму
розкладено на суму та
та  ) ;
) ; ;
; ;
; ;
; (отримано загальний розв’язок) .
(отримано загальний розв’язок) . . Цю функцію (логістичну функцію, рис. 8.1) було розглянуто в темі 4. Вона описує динаміку кількості y проданого товару залежно від часу t. Відщукання конкретних параметрів a, b та g - завдання дисципліни “Економетрія”.
. Цю функцію (логістичну функцію, рис. 8.1) було розглянуто в темі 4. Вона описує динаміку кількості y проданого товару залежно від часу t. Відщукання конкретних параметрів a, b та g - завдання дисципліни “Економетрія”. y
y
 b/a
b/a
 x
x ;
; ;
; ;
; .
. , тобто обернена функція.
, тобто обернена функція. , де U(x) - функція корисності цієї особи. Побудуємо функцію корисності для особи зі сталою (незалежною від x ) схильністю до ризику r(x)=r (як звичайно, r<0).
, де U(x) - функція корисності цієї особи. Побудуємо функцію корисності для особи зі сталою (незалежною від x ) схильністю до ризику r(x)=r (як звичайно, r<0). за умов U(0)=0, U¢(0)=k.
за умов U(0)=0, U¢(0)=k. ,
,
 = 5-5e-0,2x .
= 5-5e-0,2x .

 5
5 x
x
 (9.1)
(9.1) є збіжним. Його сума дорівнює 1, оскільки згідно з формулою суми геометричної прогресії
є збіжним. Його сума дорівнює 1, оскільки згідно з формулою суми геометричної прогресії  .
. є розбіжним, оскільки можна довести, що для будь-якого числа A знайдеться такий номер N , що
є розбіжним, оскільки можна довести, що для будь-якого числа A знайдеться такий номер N , що  .
. . Коефіцієнт
. Коефіцієнт  називають мультиплікатором.
називають мультиплікатором. ).
). і навпаки.
і навпаки. . Нехай для всіх значень індексу i виконується ai³bi . Тоді із збіжності ряду
. Нехай для всіх значень індексу i виконується ai³bi . Тоді із збіжності ряду  .Тоді при l<1 ряд збігається, а при l>1 розбігається.
.Тоді при l<1 ряд збігається, а при l>1 розбігається.

 . Ряд збігається.
. Ряд збігається. (кожні два сусідні члени ряду мають інший знак). Тоді якщо
(кожні два сусідні члени ряду мають інший знак). Тоді якщо  , то ряд є збіжним.
, то ряд є збіжним. збігається, бо
збігається, бо  .
. , тобто
, тобто  , звідки
, звідки  . Отже, потрібно взяти 100 членів ряду.
. Отже, потрібно взяти 100 членів ряду. , та умовно збіжним, якщо збігається ряд
, та умовно збіжним, якщо збігається ряд  розбігається.
розбігається. є абсолютно збіжним.
є абсолютно збіжним.
 .
. . Отже, радіус збіжності нашого степеневого ряду R=2. При –2<x<2 степеневий ряд збігається. При x>2 та x<-2 цей ряд розбігається. Випадки x=2 та x=-2 потрібно досліджувати окремо.
. Отже, радіус збіжності нашого степеневого ряду R=2. При –2<x<2 степеневий ряд збігається. При x>2 та x<-2 цей ряд розбігається. Випадки x=2 та x=-2 потрібно досліджувати окремо.
 , (9.2)
, (9.2)  .
. (9.3)
(9.3)

 ) ряд збігається при будь-якому значенні x.
) ряд збігається при будь-якому значенні x.