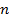|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лінійне поліноміальне згладжування
Розрахунково-графічна робота З дисципліни „Системи обробки сигналів і зображень” Варіант 18 Перевірив: Виконав: Ігнатенко В.М. ст. гр. ІК-02 Маленко М.В.
Київ – 2012
План I. Завдання II. Короткі теоретичні відомості III. Розрахунок
І. Завдання 1 Дискретизовний сигнал
Провести однократне згладжування даних ковзаючим лінійним поліномом по трьом і п’яти точках. Вирахувати значення різниць (відхилень) між значеннями вихідних і згладжених даних, знайти максимальне по модулю значення різниці та суму квадратів відхилень між вихідними та згладженими даними. Подати усі вихідні дані та результати обчислювань у відповідній табличній та графічній формі.
2 Дискретизовний періодичний сигнал
Знайти розкладання цього сигналу
ІІ. Короткі теоретичні відомості Лінійне поліноміальне згладжування. Метод ковзаючого середнього має один суттєвий недолік – зростаюча втрата даних при збільшені числа проходів згладжування. Цей недолік можна усунути якщо замість полінома нулевої степені
Оптимальні значення шуканих коефіцієнтів
що дає після перетворення таку систему алгебраїчних рівнянь:
Припускаючи, що дискрети
а в системі рівнянь (2.2.9) отримуємо такі коефіцієнти:
В результаті система рівнянь (2.2.9) перетворюється в таку:
що дає наступний розв’язок:
Оскільки значення згладжених даних тепер розраховуються по поліному
зникає різниця
Якщо поставити за мету не втрачати по два значення – одне на початку, а друге – в кінці масиву даних, то потрібно скористатися повним виразом для поліному
(2.2.14) Підставивши (2.2.11) в (2.2.14) отримуємо таке:
(2.2.15) Виходячи з аналогічних тверджень при зглажуванні по п’яти точкам можна використати наступні формули:
(2.2.24) Ряд Фур’є Кожна періодична функція може бути подана за допомогою ряду з тригонометричними функціями, тобто
де
Тобто періодична функція Вираз (1.2.1) дуже часто подається в іншій формі, як то:
відомий як ряд Фур’є. де
і звуться коефіцієнтами Фур’є функції Коефіцієнт
Якщо в (1.3.2) взяти скінченне число членів ряду Фур’є, тобто у вигляді довільного тригонометричного многочлена степені
то якщо у якості коефіцієнтів
Дійсно, якщо в (1.3.7) замість
то отримуємо систему алгебраїчних рівнянь, розв’язком якої і будуть співвідношення (1.3.3) – (1.3.5). Це є нічим іншим, ніж наближенням (апроксимацією) тригонометричним многочленом Таким чином ряд Фур’є розкладає періодичну неперервну функцію за тригонометричними функціями
ІІІ. Розрахунок Завдання 1 Згладжування лінійним поліномом по трьох і п’яти точкам. Вхідні дані:
Для згладження по трьом точкам використаємо формули:
Розрахунок:
Знайдемо відхилень між вхідними і зглаженими даними:
Максимальне відхилення:
Знаходження суми квадратів відхилень:
Для згладження по п’яти точкам використаємо формули:
Розрахунок:
Знайдемо відхилень між вхідними і зглаженими даними:
Максимальне відхилення:
Знаходження суми квадратів відхилень:
Вхідна:
За трьома точками:
За 5 точками:
Завдання 2 Вхідні данні:
Для знаходження коефіцієнтів розкладу заданої функції в ряд Фур’є, змінимо формули 1.3.3 і 1.3.4 для дискретизованого сигналу:
…
…
Таблиця коефіцієнтів
Таким чином, даний сигнал можна подати у вигляді
Графік
Поиск по сайту: |
 заданий своїми значеннями у наступній таблиці:
заданий своїми значеннями у наступній таблиці:


 заданий своїми значеннями у наступній таблиці:
заданий своїми значеннями у наступній таблиці:
 в ряд Фур’є, визначивши усі ненульові гармоніки. Результати розрахунків подати в аналітичному (формульному) і табличному вигляді, включаючи частоти гармонік і відповідних їм коефіцієнтів Фур’є-функції.
в ряд Фур’є, визначивши усі ненульові гармоніки. Результати розрахунків подати в аналітичному (формульному) і табличному вигляді, включаючи частоти гармонік і відповідних їм коефіцієнтів Фур’є-функції. використати поліном першої степені
використати поліном першої степені  , який має вже два шуканих коефіцієнта
, який має вже два шуканих коефіцієнта  та
та  ; тобто він подається у такому вигляді
; тобто він подається у такому вигляді  і задає пряму лінію. Знову ж таки вибираємо дял побудови цього поліному мінімально можливу кількість даних з вихідного масиву
і задає пряму лінію. Знову ж таки вибираємо дял побудови цього поліному мінімально можливу кількість даних з вихідного масиву  - три, записуючи квадратичну міру близькості і поліном у такому вигляді:
- три, записуючи квадратичну міру близькості і поліном у такому вигляді: (2.2.7)
(2.2.7) на
на 
 (2.2.8)
(2.2.8)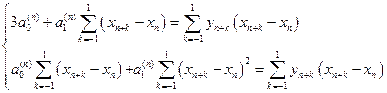 (2.2.9)
(2.2.9) рівновіддалені одна від одної з інтервалом
рівновіддалені одна від одної з інтервалом  , маємо:
, маємо:

 (2.2.10)
(2.2.10) (2.2.11)
(2.2.11) у точці
у точці  , то
, то  і у виразі
і у виразі (2.2.12)
(2.2.12) і тому залишається тільки
і тому залишається тільки  , тобто необхідно використати тільки коефіцієнт
, тобто необхідно використати тільки коефіцієнт 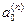 ,
,  , а значить і вирахувати тільки наступне:
, а значить і вирахувати тільки наступне: (2.2.13)
(2.2.13) і
і  , а також
, а також  і
і  відповідно, що дає:
відповідно, що дає:







 (1.3.1)
(1.3.1) - періодична функція, що визначена на відрізку
- періодична функція, що визначена на відрізку 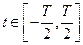 ;
; - чисельні коефіцієнти,
- чисельні коефіцієнти,  - початкова фаза,
- початкова фаза, - інтервал визначення періодичної функції
- інтервал визначення періодичної функції  , частотою
, частотою  і початковою фазою
і початковою фазою  . Для точного відтворення функції
. Для точного відтворення функції  . Ці окремі складові називаються гармоніками,а коливання з частотою
. Ці окремі складові називаються гармоніками,а коливання з частотою  - першою (основною) гармонікою (
- першою (основною) гармонікою (  ) з частотою
) з частотою  - другою гармонікою (
- другою гармонікою (  ) і т.д.
) і т.д. (1.3.2)
(1.3.2) , так що
, так що  ;
; 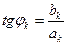 ; Коефіцієнти
; Коефіцієнти  визначаються з наступних формул
визначаються з наступних формул (1.3.3)
(1.3.3) (1.3.4)
(1.3.4) (1.3.5)
(1.3.5) (1.3.6)
(1.3.6) многочлена
многочлена  взяти відповідні коефіцієнти Фур’є функції
взяти відповідні коефіцієнти Фур’є функції  (1.3.7)
(1.3.7) (1.3.8)
(1.3.8) похибка досягає нуля.
похибка досягає нуля. , які створюють систему ортогональних та нормованих функцій. Це розкладання можна узагальнити і на випадок неперіодичної функції.
, які створюють систему ортогональних та нормованих функцій. Це розкладання можна узагальнити і на випадок неперіодичної функції.


 — 0.3083
— 0.3083

































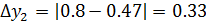

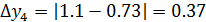

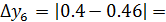 0.06
0.06