|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Визначимо щільність зв’язку між віком і відпрацьованим часом
Перевіримо істотність зв’язку: К1= 6 - 1 = 5 , К2= 28 - 6=22 Fф= 0.71 /(1- 0.71 )*22/ 5=10.78 Fкр=2,67 В даному випадку Fкр < Fф, отже зв'язок між віком і відпрацьованим часом, вважається, що він спричинений випадковими факторами.
Іншим методом визначення взаємозв’язків між факторною і результативною ознакою метод регресії і кореляції. На першому етапі при застосуванні цього методу визначають рівняння регресії. Задача регресійно-кореляційного методу полягає у виявленні зв’язку між факторною та результативною ознаками, та виборі рівняння регресії методом найменших квадратів. Це означає, що сума різниць квадратів теоретичних і емпіричних значень повинна бути мінімальною. S(Уі - У)2® min На наступному етапі необхідно знайти параметри рівняння: У = а + b*х де а – параметр, що показує значення результативної ознаки (у), якщо факторна ознака х = 0; b – параметр, що показує на скільки одиниці змінюється у середньому результативна ознака (у), якщо факторну ознаку змінити на одиницю. Для знаходження параметрів будується система рівняння: n*a + b*S x = S y a*S x + b*S x2 = S x*y Для розв’язку системи рівнянь побудуємо допоміжну таблицю. На наступному етапі проводиться оцінка щільності зв’язку. Щоб виявити щільність зв’язку, вимірюють лінійний коефіцієнт кореляції Пірсона:
Лінійний коефіцієнт кореляції r змінюється в межах - 1 < r < +1. Він показує напрямок і тісноту зв’язку між ознаками. На заключному етапі перевіряється істотність зв’язку. Fф де Κ1 = c– 1 К2 = n – c, с—кількість коефіцієнтів в рівнянні регресії.
Розглянемо взаємозв’язок між технічною швидкістю (факторна ознака) і продуктивністю праці (результативна ознака). Побудуємо кореляційне поле. Рис. 11.Кореляційне поле. Припускаємо, залежність лінійна. Побудуємо допоміжну таблицю.
Таблиця 3.8. Зв'язок між коефіцієнта використаного робочого дня (факторна ознака) і відпрацьованим часом (результативна ознака).
З системи рівнянь отримуємо рівняння регресії: 28а+ 1.034b=1698 1.034a+ 42.919b=2082.7 а=58,906 b=47,301 Функція має вигляд: Y= 58,906 + 47,301х. Відповідно до функції розрахуємо теоретичні значення результативної ознаки. Ці значення наведено в останньому стовпці табл. 3.13. За допомогою коефіцієнта кореляції Пірсона оцінимо щільність зв’язку між віком і відпрацьованим часом. XY=74,382 X=1,0346 Y=774,97
Отже, коефіцієнт кореляції має значення: r =( 74,382- 1,0346*774,97 )/( * )=+ , тому можна зробити висновок, що зв'язок є досить суттєвим, оскільки значення коефіцієнта кореляції є досить близьким до 1. Перевіримо істотність зв’язку між залишковою вартістю і кількістю їздок. К1= 2 - 1=1 К2= 28- 2 =26 Fф= / *26/1= Fкр=4,22 Таким чином, Fкр Fф, що вказує на неістотність зв’язку між віком і відпрацьованим часом.
Поиск по сайту: |
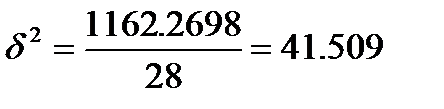
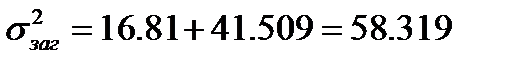
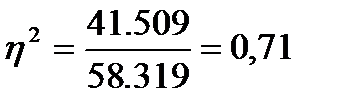 -- таким чином маємо слабкий зв'язокміж віком і відпрацьованим часом, оскільки
-- таким чином маємо слабкий зв'язокміж віком і відпрацьованим часом, оскільки 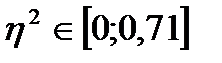 .
.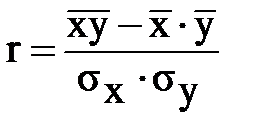

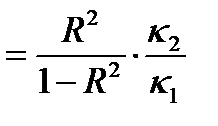 ,
,