 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Середні величини та показники варіації
При вивчені масових явищ одна з основних задач статистики є вивчення окремих властивостей кожної сукупності явища. Для того щоб виявити характерні особливості сукупності, використовують середні величини. Середня величина характеризує всю вагу одиниць сукупності. В статистиці використовують декілька видів середніх величин. Основними серед них є: середня арифметична, середня гармонійна, середня квадратична і середня геометрична. Середня арифметична – основний вид середніх величин. Буває проста і зважена. Проста – це сума індивідуальних значень варіруємої ознаки, що поділена на кількість одиниць сукупності. Зважена – середня із варіантів, що повторюється не однакову кількість раз чи має різну статистичну вагу. Середня квадратична використовується для оцінки варіації, тобто коли треба оцінити середню варіацію ознаки. Середнє гармонійне і середнє геометричне в даному випадку не знаходимо. Середня арифметична проста:
де Хі – індивідуальні значення ознаки; n ‑ кількість одиниць сукупності. Середня арифметична зважена. Оскільки сукупність згрупована, а частоти варіантів задані явно, то визначаємо середню арифметичну зважену величину:
де Хі – індивідуальні значення ознаки; mі ‑ кількість однакових варіант.
Розрахуємо середні величини: 1. Ознака –вік працівника: Таблиця 3.2.
Ця величина показує, що в середньому вік становить 37 років .
2.Ознака – відпрацьований час: Таблиця 3.3.
Середній відпрацьований час становить 60,69 год /в день.
3.Ознака – коефіцієнт використаного робочого дня : Таблиця 3.4.
Середній коефіцієнт використаного робочого часу становить 1,17 год в день .
Крім визначення середніх величин, щоб оцінити коливання ознаки сукупності, в цьому розділі роботи знаходимо показники варіації, які показують як розмістились варіанти ознаки навколо середнього значення ознаки. До них відносяться: розмах варіації, середнє лінійне відхилення, середнє квадратичне відхилення та дисперсія. Розмах варіації- становить різницю між мінімальним і максимальним значенням ознаки. Перевага показника у тому, що його знаходження дуже просте. Недолік – із всіх одиниць сукупності беруться лише 2 одиниці, що мають максимальне та мінімальне значення. Rх = xmax – xmin -- для ознаки –вік працівника: Rх = 52-21=31 років --для ознаки –відпрацьований час : Rх = 71-53,2=17,8 год/в день -- для ознаки –коефіцієнт використання робочого дня : Rх = 1,35-0,35=1 (год) Таким чином, вік працівника варіює в межах 31 років, відпрацьований час змінюється в межах 17,8 год/в день, а коефіцієнт використаного робочого дня варіює в розмірі 1 год.
Середнє лінійне відхиленняпризначене для вимірювання варіації ознаки в сукупності. Цей показник відрізняється від попереднього тим, що він враховує всі одиниці сукупності , проте є недолік: не враховується знак відхилення ознаки від середньої величини.
де хі – індивідуальне значення ознаки.
-- для ознаки – вік працівників:
Значення віку для кожного з працівників знаходиться в межах
--для ознаки – відпрацьований час :
Значення відпрацьований час знаходиться в межах
-- для ознаки – коефіцієнтом використаного робочого дня:
Значення коефіцієнтом використаного робочого дня знаходиться в межах Середнє квадратичне відхилення – корінь квадратний із середнього квадрату відхилень від середніх значень. Воно показує, на скільки в середньому індивідуальне значення ознаки відрізняється від середніх величин.
-- для ознаки – вік працівників:
Квадратичне відхилення віку працівників від його середнього становить --для ознаки – відпрацьований час :
Квадратичне відхилення відпрацьованого часу від його середнього значення становить
-- для ознаки – коефіцієнт використаного робочого дня :
Квадратичне відхилення коефіцієнта використаного робочого дня від його середнього значення становить
Дисперсія – це абсолютний показник варіації, квадрат квадрата відхилення. Зважена дисперсія визначається за формулою:
-- для ознаки – коефіцієнт використання пробігу:
--для ознаки – продуктивність праці:
-- для ознаки – технічна швидкість:
При порівнянні варіації різних ознак використовуються відносні характеристики – коефіцієнти варіації, які обчислюються як відношення абсолютних характеристик варіації до характеристики центру розподілу.
-- для ознаки – коефіцієнт використання пробігу: V= ( 10,3 / 37 )*100%=27,8 %
--для ознаки – продуктивність праці: V=( 4,1 /60,69 )*100%=6,7 %
-- для ознаки – технічна швидкість: V=( 0,3/ 1,17 )*100%= 25,6 % Вважається, що якщо V>30%- зв'язок не однорідний, V<30%- зв'язок однорідний. В даному випадку бачимо, що сукупність, розглянута в ході спостереження є однорідною. 3.3 Структурні середні Структурні середні – це середні, що характеризують структуру варіаційних рядів. До середніх структурних відносяться дві величини, які називаються "мода" і "медіана". Мода (модальна величина) ряду – це така величина, яка найбільш часто зустрічається в даному розподілі.
де x0 – це нижня межа модального інтервалу. i – довжина інтервалу. mm0 – частота модального інтервалу, mm0-1 – частота інтервалу, що передує модальному, mm0+1 – частота інтервалу, що йде після модального інтервалу.
Розрахуємо моду для таких показників:
-- коефіцієнт використання пробігу (модальний інтервал –(21-26,2)):
Найбільше в сукупності зустрічаються працівники з віком 24 роки
-- відпрацьований час (модальний інтервал –(56,1-59)):
Найбільше в сукупності зустрічаються працівники з відпрацьованим часом 57,2 год -- коефіцієнт використаного робочого дня (модальний інтервал –(1,25-1,35)):
Найбільше в сукупності зустрічаються працівники, що мають коефіцієнт використаного робочого дня 1,30 (год/в день).
Медіаною називається значення варіруючої ознаки, що знаходиться в середині ранжируємого ряду і поділяє цей ряд на дві рівні частини.
де Х0 – нижня границя медіанного інтервалу; і – величина інтервалу;
mе – частота медіанного інтервалу; Sme-1 – сума частот до медіанного інтервалу.
Розрахуємо медіану для таких показників:
-- вік працівників (медіанний інтервал –(31,4-36,6)):
У половини працівників вік більше 34,5 у іншої половини – менше 34,5.
-- відпрацьований час (медіанний інтервал –(59-61,9)):
У половини працівників відпрацьований час становить більше 60,4год, у іншої половини – менше 60,4год.
-- коефіцієнт використаного робочого дня (медіанний інтервал –(1,19-1,25)):
У половини працівників коефіцієнт використаного робочого дня становить більше 1,21 год у іншої половини – менше 1,21год.
Поиск по сайту: |
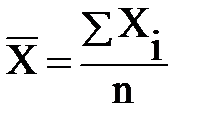
 ;
;


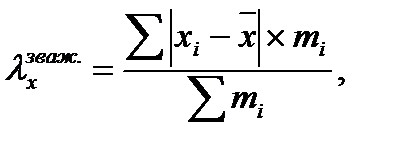
 - середнє арифметичне ознаки.
- середнє арифметичне ознаки.
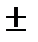 5,7 .
5,7 .
 5,2 год.
5,2 год.
 0,12 год/в день
0,12 год/в день

 10,3
10,3
 4,1 год.
4,1 год.
 0,3 год/в день.
0,3 год/в день.



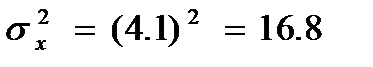






 ;
; mі – загальна сума частот усіх інтервалів;
mі – загальна сума частот усіх інтервалів;

