 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Первый замечательный предел
При вычислении пределов используется непрерывность элементарных функций в области их определения и теоремы о пределе суммы, разности, произведения и частного. Пример 1. Вычислить а) Решение. а) Так как функции и в числителе, и в знаменателе непрерывны, то В силу теоремы о пределе частного получаем
б) Здесь поэтому в) Так как Особое внимание следует уделить случаю, когда и числитель, и знаменатель стремятся к нулю при
Обращаем внимание на тот факт, что отношение Еще один рисунок наглядно показывает, как мало различаются функции
Пределу (1) можно придать другую форму, если заменить
Теорема о пределе произведения позволяет получить ещё одну форму первого замечательного предела:
Рекомендуем нарисовать графики пар функций
Все приведенные соотношения справедливы и при замене
Если при вычислении предела отношения тригонометрических функций возникает неопределённость вида
Пример 2.Вычислить Решение.
Можно и не записывать замены аргумента, а просто уравнивать коэффициенты:
Пример 3.Вычислить Решение. Пример 4.Вычислить Решение. К первому замечательному пределу приводит формула
Пример 5.Найти предел дроби Решение. а) б)
Пример 6.Вычислить Решение. Здесь тоже необходима замена:
Пример 7.Вычислить Решение. Здесь можно было ввести новую переменную
Пример 8.Вычислить Решение. После избавления от иррациональности получаем первый замечательный предел:
Поиск по сайту: |
 ; б)
; б)  ; в)
; в)  .
. ,
,  .
. .
. ,
, .
. - числитель стремится к конечному и отличному от нуля пределу, а
- числитель стремится к конечному и отличному от нуля пределу, а  - знаменатель в точке
- знаменатель в точке 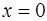 является бесконечно малой функцией, то частное в этой точке - бесконечно большая функция:
является бесконечно малой функцией, то частное в этой точке - бесконечно большая функция:  .▲
.▲ , т.е. частное представляет в этой точке неопределённость вида
, т.е. частное представляет в этой точке неопределённость вида  .
. Теорема. Предельное значение функции
Теорема. Предельное значение функции  в точке
в точке  . (1)
. (1) к нулю. Это наглядно представлено на графике функции
к нулю. Это наглядно представлено на графике функции 
 в окрестности точки
в окрестности точки 
 . Тогда
. Тогда ,
,  при
при  , поэтому
, поэтому или
или  .
. . Значит, и
. Значит, и  .
. И снова обращаем внимание на тот факт, что отношение
И снова обращаем внимание на тот факт, что отношение  стремится к единице только при стремлении аргумента
стремится к единице только при стремлении аргумента  .
. Еще один рисунок наглядно показывает, как мало различаются функции
Еще один рисунок наглядно показывает, как мало различаются функции  в окрестности точки
в окрестности точки  и
и  ;
;  и
и  =0.
=0. , если
, если  при
при  :
:


 .
. .▲
.▲
 .▲
.▲ .
. :
: .▲
.▲ а) при
а) при 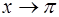 .
. .
. . Здесь аргумент
. Здесь аргумент  , т.е. сделаем замену
, т.е. сделаем замену  . Тогда при
. Тогда при 
 ▲
▲ .
.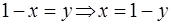 , при
, при  новая переменная
новая переменная  .▲
.▲ .
. , которая стремится к 0 при
, которая стремится к 0 при  . Но мы предлагаем преобразовать разность синусов в произведение:
. Но мы предлагаем преобразовать разность синусов в произведение:
 ▲
▲ .
.
 ▲
▲