 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Некоторые приемы вычисления пределов
1) Неопределённость вида Пример 1. Покажем, что в каждой точке Решение. Действительно, в силу теоремы о пределе произведения
а) Решение. а). Согласно предыдущему
В силу теоремы о пределе частного (мы вправе её применить, т.к. предел знаменателя отличен от нуля) запишем:
б). В этом случае Найдем предел знаменателя: В результате получаем бесконечно малую в точке
в). Здесь в точке
Пример 3. Найти предел алгебраической дроби Решение. Т.к. и
Пример 4. Найти предел дроби Решение . Здесь, как и в предыдущем примере, в точке
Поэтому выделим в числителе и в знаменателе множитель
Переходя к общему случаю, изучим поведение отношения двух многочленов
при стремлении переменной
Поэтому в случае
Если Нас особенно интересует случай, когда и Пример 5. Вычислить Решение. И в числителе, и в знаменателе «носителем нуля» является множитель В знаменателе разность кубов представим как произведение разности первых степеней на неполный квадрат суммы: Получаем
Пример 6. Вычислить Решение. И в числителе, и в знаменателе «носителем нуля» является множитель
Здесь сумма кубов представлена как произведение суммы первых степеней на неполный квадрат разности. В знаменателе Получаем
Пример 7.Вычислить Решение. И в числителе, и в знаменателе «носителем нуля» является множитель
В знаменателе: Значит, Сокращаем на множитель
Пример 8. Вычислить Решение В числителе множитель
После сокращения на множитель
Пример 9. Вычислить Решение . И здесь воспользуемся биномом Ньютона:
Теперь легко выделить множитель
Поиск по сайту: |
 . Отношение многочленов.
. Отношение многочленов. бесконечной прямой функция
бесконечной прямой функция  имеет предельное значение, равное
имеет предельное значение, равное  .
. а в силу теоремы о пределе суммы
а в силу теоремы о пределе суммы ▲ Пример 2. Найти предел алгебраической дроби
▲ Пример 2. Найти предел алгебраической дроби  , когда
, когда б)
б)  в)
в) 


 , т.е. в точке
, т.е. в точке  числитель - бесконечно малая функция.
числитель - бесконечно малая функция.

 числитель имеет конечный и отличный от нуля предел:
числитель имеет конечный и отличный от нуля предел:  а знаменатель в этой точке - бесконечно малая функция:
а знаменатель в этой точке - бесконечно малая функция:  . В результате получаем бесконечно большую в точке
. В результате получаем бесконечно большую в точке  ▲
▲
 и
и  то получаем неопределённость вида
то получаем неопределённость вида  , а затем (вспоминая, что в определении предела функции аргумент
, а затем (вспоминая, что в определении предела функции аргумент  , но
, но  ) сократим на отличный от нуля множитель
) сократим на отличный от нуля множитель  . Окончательно получаем
. Окончательно получаем .▲
.▲ при
при  .
. и числитель, и знаменатель являются бесконечно малыми функциями:
и числитель, и знаменатель являются бесконечно малыми функциями: .
. , с полным правом (
, с полным правом (  но
но  ) сократим на него и перейдём к пределу:
) сократим на него и перейдём к пределу: .▲
.▲
 к конечному числу
к конечному числу  . Повторяя рассуждения, приведенные в примере 1, легко получить, что предельное значение многочлена в точке
. Повторяя рассуждения, приведенные в примере 1, легко получить, что предельное значение многочлена в точке  существует и равно его частному значению в этой точке:
существует и равно его частному значению в этой точке:

 имеем право воспользоваться теоремой о пределе частного:
имеем право воспользоваться теоремой о пределе частного: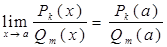 .
. , но
, но  , то при приближении
, то при приближении  неограниченно увеличивается:
неограниченно увеличивается:  .
. , и
, и  представляет собой неопределённость вида
представляет собой неопределённость вида  (верно и обратное утверждение). Значит, для раскрытия неопределённости надо и в числителе, и в знаменателе выделить «носитель нуля» - бесконечно малую в точке
(верно и обратное утверждение). Значит, для раскрытия неопределённости надо и в числителе, и в знаменателе выделить «носитель нуля» - бесконечно малую в точке  .
. . Выделим этот множитель. В числителе вынесем за скобки
. Выделим этот множитель. В числителе вынесем за скобки  и представим разность квадратов как произведение разности первых степеней на сумму первых степеней:
и представим разность квадратов как произведение разности первых степеней на сумму первых степеней:  .
.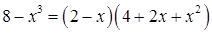 .
. . После сокращения на множитель
. После сокращения на множитель  .▲
.▲ .
. . Выделим этот множитель в числителе:
. Выделим этот множитель в числителе: .
. .
. . После сокращения на множитель
. После сокращения на множитель 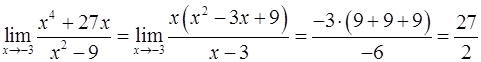 .▲
.▲ .
. . Выделим этот множитель в числителе:
. Выделим этот множитель в числителе:

 .
. и вычисляем предел:
и вычисляем предел: ▲
▲ .
. по биному Ньютона:
по биному Ньютона:  . Тогда
. Тогда .
. получаем
получаем

 .
. ▲
▲