 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сходящиеся последовательности ⇐ ПредыдущаяСтр 4 из 4
Определение 1. Число При этом пишут: Последовательность, у которой существует предел, называется сходящейся.Последовательность, не являющаяся сходящейся, называется расходящейся. С помощью кванторов
Интервал
Определение 2. Число Таким образом, конечное число элементов последовательности не влияет ни на существование ее предела, ни на его величину. Теорема(единственность предела). Сходящаяся последовательность имеет единственный предел. В связи с определением 1 всякая бесконечно малая последовательность Бесконечно большую последовательность Естественно, понятия сходящейся и бесконечно малой последовательности связаны между собой. Определение 3. Последовательность Из этого определения следует, что любой элемент
где Пример 1. Пусть Решение. Представим Теорема (необходимое условие сходимости). Если последовательность сходится, то она ограничена. Пример 2. Доказать, что последовательность Решение. Докажем, что данная последовательность не ограничена. Так как
Поиск по сайту: |
 называется пределом последовательности
называется пределом последовательности  , если для любого положительного числа
, если для любого положительного числа  найдется такой номер
найдется такой номер  , зависящий от
, зависящий от  выполняется неравенство
выполняется неравенство , равносильное
, равносильное 
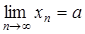 или
или 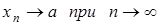 .
. и
и 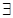 определение записывается так:
определение записывается так:
 называют
называют  , если в любой
, если в любой  - окрестности точки
- окрестности точки  является сходящейся и имеет своим пределом число 0:
является сходящейся и имеет своим пределом число 0:  .
.  .
. является бесконечно малой.
является бесконечно малой. сходящейся к числу
сходящейся к числу  , (1)
, (1) – элемент бесконечно малой последовательности.
– элемент бесконечно малой последовательности.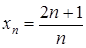 . Докажем, что
. Докажем, что  .
. в виде суммы:
в виде суммы:  . Здесь второе слагаемое
. Здесь второе слагаемое  есть элемент бесконечно малой последовательности. В силу определения 3 данная последовательность сходится к числу
есть элемент бесконечно малой последовательности. В силу определения 3 данная последовательность сходится к числу  . ▲
. ▲ расходится.
расходится. для всех номеров
для всех номеров  , начиная с первого, то
, начиная с первого, то  . Возьмем произвольное число
. Возьмем произвольное число  . Для любого номера
. Для любого номера  , соответствующий элемент последовательности
, соответствующий элемент последовательности  удовлетворяет неравенству
удовлетворяет неравенству  . Это означает, что последовательность
. Это означает, что последовательность