 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачи для самостоятельного решения. Найти дифференциал функции:
Найти дифференциал функции: 65. 69. Выразить дифференциал сложной функции через независимую переменную и ее дифференциал: Найти дифференциалы следующих неявно заданных функций: 70. 72. Найти приближенное значение приращения функции 73. Вычислить приближенно: а) 74. Вычислить приближенно: 75. Теоремы о дифференцируемых функциях Теорема Ролля.Пусть функция Теорема Лагранжа.Пусть функция Теорема Коши.Пусть функции
Задачи для самостоятельного решения
76. Проверить справедливость теоремы Ролля для функции 77. Объяснить, почему для функции 78. Написать формулу Лагранжа для функции 79. Проверить справедливость теоремы Лагранжа для функции 80. Записав формулу Коши для 81. Проверить справедливость формулы Коши для функций Правило Лопиталя - Бернулли Правило Лопиталя позволяет раскрывать неопределенности типа Теорема Лопиталя.Пусть функции Замечание. 1) Правило применимо и в случае, когда 2) Если производные 3) Предел отношения функций может существовать, но не вычисляться по правилу Лопиталя. Рассмотрим Пример.Найти Ñ Имеем Пример. Найти Ñ Применим правило Лопиталя, предварительно заменив
Пример. Найти Ñ Имеем неопределенность типа
Пример. Найти Ñ Имеем неопределенность типа =
Поиск по сайту: |
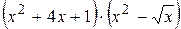 . 66.
. 66. 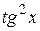 . 67.
. 67.  . 68.
. 68.  .
.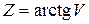 ,
,  .
. . 71.
. 71. 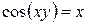 .
. при изменении
при изменении  от
от 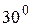 до
до 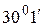 . Чему равен
. Чему равен 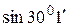 ?
?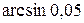 ; б)
; б) 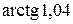 ; в)
; в)  .
.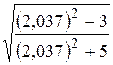 .
.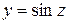 ,
, 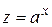 ,
, 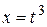 . Выразить
. Выразить  через а)
через а) 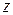 и
и  , б)
, б)  , в)
, в) 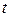 и
и  .
.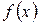 непрерывна на
непрерывна на 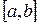 , дифференцируема на
, дифференцируема на  и
и 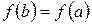 . Тогда существует, по крайней мере, одна точка
. Тогда существует, по крайней мере, одна точка  такая, что
такая, что  .
.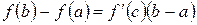 .
. непрерывны на
непрерывны на 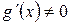
 . Тогда существует, по крайней мере, одна точка
. Тогда существует, по крайней мере, одна точка 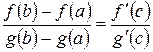 .
.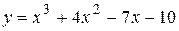 в интервале
в интервале 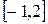 .
. , принимающей равные значения на концах отрезка
, принимающей равные значения на концах отрезка 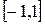 , не выполняется теорема Ролля.
, не выполняется теорема Ролля.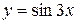 в интервале
в интервале 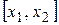 .
. в интервале
в интервале 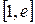 .
.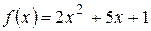 и
и  на отрезке
на отрезке 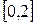 , найти значение
, найти значение  .
. и
и  на отрезке
на отрезке 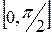 .
.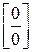 и
и 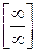 .
. , за исключением быть может самой точки
, за исключением быть может самой точки 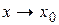 (либо бесконечно большими при
(либо бесконечно большими при 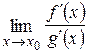 , то существует
, то существует  и имеет место равенство:
и имеет место равенство: 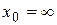 .
.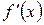 и
и 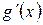 удовлетворяют условиям теоремы Лопиталя, то к ним опять может быть применено это правило.
удовлетворяют условиям теоремы Лопиталя, то к ним опять может быть применено это правило.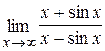 . Предел существует, так как
. Предел существует, так как 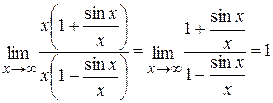 . Однако для производных
. Однако для производных 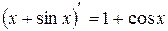 и
и  предел при
предел при 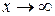 не существует, и, следовательно, не существует предел отношения этих производных.
не существует, и, следовательно, не существует предел отношения этих производных. .
.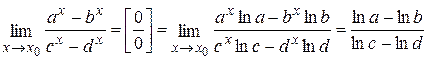 . #
. #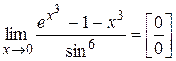 .
. на эквивалентную ей при
на эквивалентную ей при  бесконечно малую функцию
бесконечно малую функцию 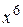 .
.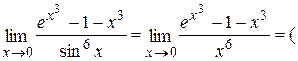 применяя правило Лопиталя)=
применяя правило Лопиталя)=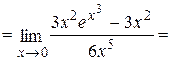

 при
при  .#
.# .
.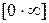 . “Перестроим” функцию:
. “Перестроим” функцию: 
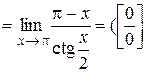 применяем правило Лопиталя)=
применяем правило Лопиталя)= 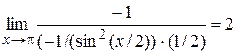 .#
.#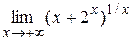 .
.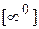 . Логарифмируя функцию
. Логарифмируя функцию 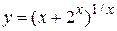 , получаем
, получаем 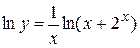 .
. 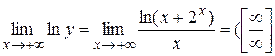 , применяем правило Лопиталя)=
, применяем правило Лопиталя)= 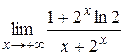 ==
==  , еще раз применяем правило Лопиталя)=
, еще раз применяем правило Лопиталя)=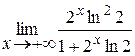 =
= 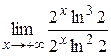 =ln 2. Следовательно,
=ln 2. Следовательно, 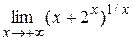 = =
= = 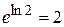 .#
.#