 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачи для самостоятельного решения. 54. Применить формулу Лейбница для вычисления производной: .
43. 45. 48. 51. 53. 54. Применить формулу Лейбница для вычисления производной: Геометрический и механический смысл производной
 функции функции 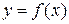 есть тангенс угла наклона касательной есть тангенс угла наклона касательной  , проведенной к графику функции в точке , проведенной к графику функции в точке  , к положительному направлению оси абсцисс , к положительному направлению оси абсцисс
 в точке в точке 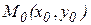 имеет вид имеет вид 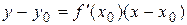 . .
Нормалью к графику функции Ее уравнение: Углом между кривыми в их общей точке называется угол между касательными, проведенными к кривым в этой точке. Механический смысл производной: Если закон движения материальной точки описывается функцией Пример.Написать уравнения касательной и нормали к графику функции Ñ Пример.Написать уравнение касательной к кривой Ñ Вычислим
Пример.Найти угол под которым пересекаются кривые Ñ Найдем точки пересечения кривых Угол
Пример.Тело массой 4 движется прямолинейно по закону Ñ Найдем скорость Тогда кинетическая энергия есть
Задачи для самостоятельного решения
55. В каких точках угловой коэффициент касательной к кубической параболе 56. При каком значении независимой переменной касательные к кривым 57. Составить уравнение касательной и нормали к линии 58. Составить уравнение нормали к линии 59. Найти угловой коэффициент касательной к линии 60. Составить уравнение касательной и нормали к линии В следующих задачах найти углы, под которыми пересекаются линии. 61. 63. 64. Сторона квадрата увеличивается со скоростью Дифференциал Функция Необходимым и достаточным условием дифференцируемости функции в точке является существование у функции производной в данной точке, при этом справедливо равенство Дифференциалом функции Свойства дифференциала. Пусть 1. 3. 5. Пусть
 в точке в точке 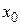 есть приращение ординаты касательной, проведенной к графику функции в точке есть приращение ординаты касательной, проведенной к графику функции в точке  , при приращении аргумента равном , при приращении аргумента равном  . .
(Рис. 1).При откуда получаем формулу приближенного вычисления значения функции в точке. Пример.Найти дифференциал функции Ñ Перепишем функцию
Пример.Вычислить приближенно Ñ Выберем точку Дифференциалом второго порядка функции
Соответственно дифференциал n-ого порядка Дифференциалы 2-го и более высоких порядков сложных функций не обладают свойством инвариантности.
Поиск по сайту: |
 44.
44. 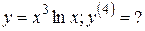
 46.
46.  47.
47. 
 49.
49.  50.
50.  Найти
Найти  .
. 52.
52. 

 .
.
 . (Рис. 1).
. (Рис. 1).  в точке
в точке 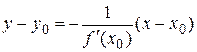 .
.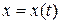 , то
, то  есть скорость, а
есть скорость, а  - ускорение этой точки в момент времени t.
- ускорение этой точки в момент времени t. в точке
в точке  .
. ,
,  . Тогда
. Тогда 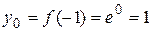 ,
,  .Составим уравнение касательной
.Составим уравнение касательной  к графику .
к графику .  ,
, 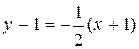 или
или  ,
,  .#
.# ,
, 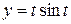 в точке
в точке  .
. . Тогда
. Тогда  ,
, 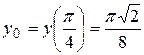 ,
, . Уравнение касательной имеет вид:
. Уравнение касательной имеет вид:  .#
.#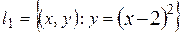 и
и 
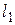 и
и 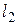 . Из равенства
. Из равенства 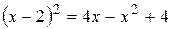 находим точки пересечения
находим точки пересечения  ,
,  . Вычислим угловые коэффициенты
. Вычислим угловые коэффициенты  и
и  касательных к кривым
касательных к кривым  .
. 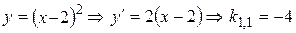 ,
, 
 между касательными определяем по формуле
между касательными определяем по формуле . В точке
. В точке  имеем соответственно
имеем соответственно  и
и  . Тогда
. Тогда  и
и  . #
. # . Определить кинетическую энергию тела в момент времени
. Определить кинетическую энергию тела в момент времени 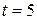 .
. в момент времени
в момент времени 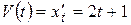 ,
,  .
. .#
.# равен 3?
равен 3?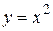 и
и  в точке с абсциссой
в точке с абсциссой  .
. в точке с абсциссой
в точке с абсциссой  .
.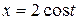 ,
,  в точке
в точке  .
.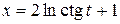 ,
,  при
при  .
. и
и 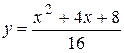 . 62.
. 62. 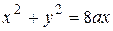 и
и  .
.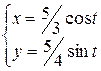 .
. . Какова скорость изменения периметра и площади квадрата в тот момент, когда его сторона равна
. Какова скорость изменения периметра и площади квадрата в тот момент, когда его сторона равна  ?
? , если ее приращение
, если ее приращение  в этой точке может быть представлено в виде
в этой точке может быть представлено в виде  , где
, где  - постоянная, не зависящая от
- постоянная, не зависящая от  - бесконечно малая величина при
- бесконечно малая величина при  .
. .
. .
.  .
.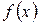 и
и 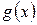 дифференцируемые функции. Тогда справедливы равенства:
дифференцируемые функции. Тогда справедливы равенства: , с – постоянная. 2.
, с – постоянная. 2.  .
. . 4.
. 4.  ,
, 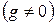
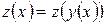 сложная функция, образованная композицией дифференцируемых функций
сложная функция, образованная композицией дифференцируемых функций  и
и 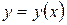 . Тогда
. Тогда 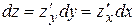 . Эти равенства выражают свойство инвариантности формы первого дифференциала.
. Эти равенства выражают свойство инвариантности формы первого дифференциала. Геометрический смысл дифференциала.
Геометрический смысл дифференциала.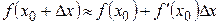
 имеем
имеем  ,
,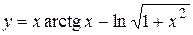 .
. в виде
в виде  . Найдем
. Найдем 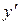 .
. . Тогда
. Тогда  .#
.# .
.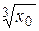 был легко вычисляем, а
был легко вычисляем, а 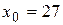 ,
,  . Для функции
. Для функции 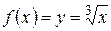 имеем:
имеем:  ,
,  ,
, 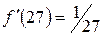 . Тогда
. Тогда 
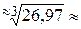

 .#
.# и он обозначается
и он обозначается  или
или  .
.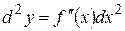
 ,
,  .
.