 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Напряжения в целике. Способ автора
Изложенные в § 60 способы расчета имеют в виду в основном распределение нагрузки на целик, а не напряжения в нем. Между тем, решающее значение для устойчивости стенок целика и прочности его в целом имеет именно распределение напряжений. В этом отношении нужно отметить экспериментальное (с помощью оптического метод 1) изучение напряжений в целиках Л. Г Афендиком [70] и приближенное теоретическое решение задачи, принадлежащее Ц. О. Левиной и С. Г. Михлину [71]. Ввиду важности вопроса и эффективности полученных результатов остановимся на этом решении подробнее. Горные породы рассматриваются как упругие, однородные и изотропные, а массив в целом — как бесконечное полупространство. Считается, что две одинаковые камеры, расположенные на одном горизонте, имеют каждая бесконечно большую длину (условия плоской задачи), высота их мала по сравнению с шириною и что поперечное сечение имеет форму о^ала, вписанного в прямоугольник или трапецию (фиг. 57). Наличие пустот (камер) в тяжелой полуплоскости изменяет первоначальное напряженное состояние Это изменение особенно значительно вбдизи пустот. Однако оио_быстро_убывает по мере удаления от них. Добавочные напряжения ох, ау и обусловленные наличием пустот, по мере удаления от последних быстро убывают и на бесконечности равны нулю. Полные компоненты напряжения равны: а = a(J) 4-7 а «= а*0) 4-7 т = т(°> 4- 7 г X ~ г> У у I У > ху — ху I гу> где <з(°>, — компоненты первоначального (при отсутствии пустот) напряжения.
Задача формулируется так: требуется найти величину з ц т^] непрерывные в области фиг. 57, такими образом, чтобы на бесконе^ ности они обращались в нуль. Эти величины должны удовлетворять уравнениям равновесия и совместности, а также ^оНтурным условиям: ал ■ cos (v, х) -J- Г~у • cos (v,jy) '= «у (у -f Н) cos (v, x), > cos (V, x)-\-7y . Cds (v,_y) = Y (У + H)cos(v,j>), где v — направление нормали к коцтуру, а я — коэфициент бокового распора. Эти условия на границе полуплоскости упрощаются и имеют вид: __ а, • COS (v, X) + ixy ■ COS (v,y)^0, • COS (х) -j- з^ • COS (v, у) = 0. х —1
I I t « I * ч
Фиг. 57. Схема к определению напряжений в целике С целью упрощения вычислений вводится еще ряд ограничений, допустимых при условии значительной глубины заложения камер и малой их высоты по сравнению с этой глубиною (//^у + Я и др.). Задача решается с помощью теории конформного преобразования. В результате получены весьма громоздкие формулу, требующие при их применении большой вычислительной работы, а потому неуловимые для практического пользования. Эти формулы здесь не приводятся, читатель их может найти в источнике [71]. Дополнительными исследованиями полученные результаты были уточнены Ц. О. Левиной [72]. Основные выводы, иллюстрируемые числовыми примерами (табл. 30 и 31), сводятся к следующим: 1) оси xi и у являются осями главных нормальных напряжений, и, таким образом, для точек на Них ху П М. Цимбаревич / 2) всходу, в пределах целика, нормальные напряжения' <зх я чу являютсй сжимающими; 3) по мере удаления от середины целика (табл. 30) напряжение з возрастает по абсолютной величине, оставаясь сжимающим, при этом наименьшее его значение (в середине целика) вообще значительно превышает вес вышележащих пород; что же касается сжимающего нормального напряжения <зх, то величина его также возрастает/ однако до некоторого максимума, а затем уменьшается; в связи с указанным величина напряжения "max по мере удаления от середины целика возрастает, достигая максимума на боковой поверхности целика (табл 30), Таблица 30
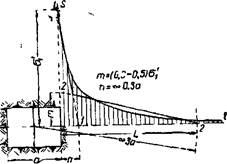
4) величина напряжения о в центре целика практически не зависит от ширины камеры L или ширины целика В, а зависит только от их отношения I = . При этом, чем больше это отношение, тем больше напряжение зу (табл. 31). То же относится и к напряжению <5Х. Что же касается напряжения т„1ах, то его величина при этом в центре понижается (табл. 31). Из изложенного следует, что междукамерный целик находится при плоской задаче в условиях двухосного сжатия. Наиболее опасными местами в отношении устойчивости и прочности являются стенки целика, где напряжения чу и imdX достигают наибольших значений. Здесь прежде всего следует ожидать появления пластической деформации, т е. нарушения устойчивости обнажения, что нередко и наблюдается на практике. Ниже приводится приближенный способ расчета напряжений в целиках и самих целиков, принадлежащий автору этого труда. Имеются в виду целики между горизонтальными выработками разных или одинаковых форм и размеров поперечного сенения. Породы считаются изотропными и однородными. Задача рассматривается как плоская. На основании данных А. Н. Динника и др. [63], допускается, что радиус области, которая окружает выработку и в которой имеют В стенке горизонтальной выработки происходит затухание добавочных напряжений зтах (oj) по закону некоторой кривои st (фиг 58) Эта кривая имеет крутую часть v контура сечения выработки и пологую часть, которая асимптотически приближается к горизонтальной оси. Чем больше k — коэфициент концентрации напряжений ашах на контуре сечения, тем более резко отмечается его уменьшение, а, следовательно, и уменьшение добавочных напряжений по мере удаления от контура [63] Для упрощения расчетов заменим кривую st на фиг. 58 двумя прямыми: 1 — 1 и 2 — 2, которые возможно ближе приближались бы Фиг 58. Эскиз к расчету опорного дав- к крутой и пологой частям кри- ления вой st. Величины отрезков отсекаемых этими прямыми на вертикальной и горизонтальной осях, обозначим в долях от (k—1) и а через тип. Числовые значения этих величин приближенно могут быть установлены по данным распределения напряжений вокруг выработки [63] Ниже для расчетов принимается: т = (0,2 — 0,5) (k— 1) п = (0,3-:- 0,6) а. Заметим, что величиною п почти не приходится пользоваться. Введем следующие обозначения (фиг. 59): at и а2 — ширина выработок, Z.J и Ц — линейный размер областей влияния выработо<, считая от стенок, В — ширина целика, и а"— добавочные напряжения на контуре сечения выработок, посредине стенок, действующие в вертикальном направлении, kx и — коэфициенты концентрации напряжений атах в тех же местах, т' и т" — величины, относящиеся к эпюрам добавочных напряжений для двух выработок, и z — глубина расположения последних
На основании изложенного имеем:
Рассмотрим наиболее общий случай, когда имеет место нерлвен-
C I во
к >В. В эюм случае по всей ширине целика добавочные напряжения з( и з" накладываются друг на друга (фиг 59). На основании про- стейших геометрических соображений, йблучаем, что эти напрйжё- ния составляют на краях сечения: левой выработки <з\ т"<з" — j правой выработки aj -f-rn'o', и в точке пересечения эпюр: __ ZjLt + Lt-B)
и от правой выработки на расстоянии ч
О 2т"<
Полные же напряжения в тех же местах с учетом (1,61) и (2,61) будут: (3,61) (4,61) L ' J » Из (3,61) — (5,61) следует, что с уменьшением отношения — напряжения о< >, of и з(, увеличиваются. Они увеличиваются и с увеличением коэфициентов концентрации напряжений, т. е. с увеличением ширины выработок. Если обе выработки одинаковы (а = ах = аъ k — kx = k., и т = — т'±=т"), то формулы (3,61) и (4,61) заменяются одной ,<;>«-+ «(*_ 1) (l - -2^-)] jz, (6,61) а формула (5,61) принимает более простой вид- «е —[o,4«(ft—1) (5,0--§-) + l]Тг- (7,61) Нетрудно показать, что в рассмотренных случаях имеют место соотношения: а^а'') и ac<of>. Таким образом, распределение напряжений по ширине целика является неравномерным. Если при прямоугольном сечении углы имеют достаточные закругления, то напряжения ашах являются основными для расчета целика. Наибольшего значения они достигают на контуре сечения выработки. Что же касается главных нормальных напряжений сжатия зш1п(а,), действующих в горизонтальном направлении, то они на контуре сечения выработок, посредине стенок, раЕны нулю и постепенно увеличиваются в направлении к середине цеЛика [63]. При этом коэфициент концентрации их меньше единицы. Решающим для расчета целика является главное касательное напряжение tmax, наибольшее значение которого относится к контуру сечения выработок. Здесь _ 'max amin________ gmax ^max------- g — 2— Имея в виду гипотезу I лавных касательных напряжений, для устойчивости стенок целика необходимо соблюдение условия При соблюдении этого условия деформации целика не будут выходить из пределов упругости. Нужно заметить, что вообще целики как мероприятие по приданию устойчивости выработкам действительны лишь при соблюдении условия fttYz(ft2Tz)<o,. (9,61) Если условие (961) не соблюдается, то требуется рудничная крепь Все изложенное относилось к случаю (а), названному общим. Возможны следующие частные случаи: Ll>B>Ll, (б) 2B>L1+Li>B, (в) B>Li + Lt. (г) В случае (б) наложение добавочных напряжений друг на друга происходит лишь вблизи одной из выработок, а именно: при например вблизи правой выработки (фиг. 60). Здесь на-
i г
пряжения на краю сечения определяются по формуле (4,61). Напряжения же на краю сечения левой выработки составляют Чго же касается напряжений <з(, то они определяются по форму- ie (5,61) В случае (в) наложение напряжений происходит лишь в средней части цетика (фиг. 61). Здесь а*'» — k^Z и df> = kt -fZ, а напряжения ас определяются по формуле (5,61).
Наконец, в случае (г) наложения добавочных напряжений совсем не происходит.
При всем вышеизложенном предполагалось, что выработки могу! иметь, кроме кругового и эллиптического, также и прямоугольное сечение. Между тем в последнем случае на практике потолок выра- ( оток обычно обрабатывается по форме свода Замена такого сечения собственно прямоугольным с закругленными углами, очевидно, идет в запас при расчете (^ 55) Числовой пример Возьмем две выработки 2,5 5,0 м (1:2) и 2,5-3,75 м (1:1) Пусть г = 120 м и 7 — 2,5 т/м? На основании данных табл 26 вычисляем с помощью интерполяции hi = 1,65 и k2 = 1,48 Примем далее т' — т" = 0,4. Положим В = 8 м. Тогда имеем 2,5.5,0-1- 2,5 3,75 ^ „ п --------- 2-------- >8Д Пользуясь формулами (3 61) — (5,61), получаем з[ > = 50,4 кг/смя(Р = 47,2 кг/см2 и ос - 38,6 щсм* Если для данной породы, например, Зу = 60 кг/см2, то условие (8,61) соблюдается. ГЛАВА VII ГОРНОЕ ДАВЛЕНИЕ § 62. Состояние вопроса Горному давлению посвящена обширная литература. Перечни ее, помещенные в работах Евдокимова-Рокотовского [73], Леонтовского [74], Ростовцева [75] и др., включают сотни наименований. Исчерпывающий обзор этой литературы здесь опускается. Автор ограничивается лишь основным, что представляет интерес в настоящее время Вопросы горного давления непосредственно изучаются уже свыше 10Э лет. Девятнадцатый век, как известно, был ознаменован расцветом теории В частности, широко была разработана теория упругих яв- лений, которая была связана с началами термодинамики и математической физики, На этой основе получила широкое развитие строительная механика и, в частности, сопротивление материалов. Методы исследования и расчетные приемы, эффективно применяемые в этих отраслях знания, были привлечены и для изучения горного давления Появились многочисленные теории горного давления. Техника разработки месторождений полезных ископаемых в прошлом веке, по сравнению с современной, находилась на низком уровне. При разработке пластовых месторождений, в частности угольных, применялись забои малой ширины с ручными работами. В связи с этим характер проявления горного давления и его величина не представляли факторов, сколько-нибудь значительно влияющих на технику и экономику разработок, и простейшие теории в основном были достаточны для объяснения тех или иных явлений. Однако с заменой в забоях ручной работы машинной, в особенности с появлением врубовых машин, что относится к первой четверти текущего века, положение вещей в корне изменилось. Ширина очистных выработок, например, значительно увеличилась и достигла сотен метров. Скорость подвигания забоев также значительно увеличилась. Прит работах с обрушением в движение начали приводиться огромные массы окружающих пород, и вопросы горного давления приобрели особую остроту. Возникла сложная проблема управления горным давлением, и предложенные ранее теории горного давления оказались в новых условиях недостаточными. С целью изучения проблемы начади широко применяться опытные наблюдения, экспериментальные исследования с привлечением новейших средств изучения явлений (модели- |эдвание, оптический и сейсмический методы и др.). Появились новые теории горного давления, Однако, несмотря на все указанное, учение о горном давлении р современном своем состоянии все е<де находится на опытном пути. ЭтОт этап не пройден, и еще не создано единой стройной теории. Основная причина этого — сложность явления, в котором участвует множество влияющих факторов, комбинирующихся между собой в различных взаимосочетаниях. В последующем автор стремится внести в учение о горном давлении новые ^представления, устраняющие, по его мнению, некоторые из существующих противоречий и позволяющие наиболее объективно оценивать явления, связанные с горным давлением. § 63. Определения Устойчивые обнажения горных пород в выработках не требуют крепления, и незакрепленные выработки стоят, выполняя свое назначение. Иначе обстоит вопрос в случаях, когда обнажения неустойчивы. Здесь для поддержания выработки нужны искусственные мероприятия, в частности наиболее Ишроко применяемое мероприятие —рудничная крепь. Непосредственное назначение рудничной крепи заключается в предупреждении или уменьшении деформаций обнажения с тем, чтобы они не приняли опасных размеров. Рудничная крепь препятствует развитию этих деформаций и при этом сама деформируется. Деформация крепи — следствие механического воздействия на последнюю горной породы, называемого давлением горных пород на рудничную крепь, или, короче, горным давлением. Деформации крепи под влиянием горного давления не должны выходить из пределов прочности материала крепи В этом случае горная выработка, как сооружение, будет устойчивой. Таким образом, следует различать устойчивость обнажения и устойчивость выработки как сооружения >■ Если деформации крепи под влиянием горного давления с течением времени не выходят из пределов упругости, то крепь называется жесткой. В противном случае крепь является податливой. В зависимости от конструкции и материала, податливая крепь испытывает пластические деформации своих частей или изменения своей формы в целом, сохраняя, однако, при всем этом свою несущую способность К искусственным мероприятиям по поддержанию подземных выработок в устойчивом состоянии, кроме рудничнсй крепи, относится также оставление предохранительных целиков и предохранительных толщ (потолочных, почвенных). Целики и предохранительные толщи испытывают так же, как[и крепь, горное давление и так же, как и крепь, деформируются. Однако здесь деформации могут быть допущены только упругие. В этом — существенное отличие этих мероприятий от рудничной крепи Из изложенного следует, что термин „горное давление" следует' также понимать и более широко, чем давление горных пород на рудничную крепь. Под влиянием горного давления может находиться не только рудничная крепь, но и предохранительные целики и толщи, стенки выработок и т. п. В этом более широком смысле горное давление — объёмная сила, которой обязаны деформации рудничной крепи и обнажений горных пород в выработках, « i V»
Поиск по сайту: |


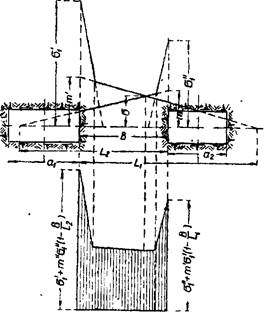 Фиг. 59, Эскиз к определению ширины целика (случай а). Эта точка отстоит от левой выработки на расстоянии, равном
Фиг. 59, Эскиз к определению ширины целика (случай а). Эта точка отстоит от левой выработки на расстоянии, равном

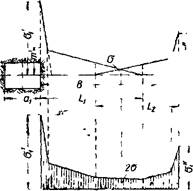
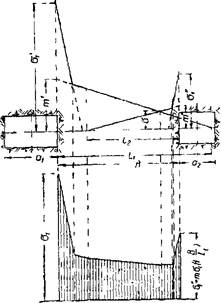 Фш 60 Эскиз к определению ширины целика (случай 6)
Фш 60 Эскиз к определению ширины целика (случай 6)