 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Продолжение таблицы 4
Продолжение таблицы 4.
ЛАБОРАТОРНАЯ РАБОТА 5. Вычисление определенных интегралов с заданной точностью. Обычно при вычислении интегралов заранее известна точность, с которой необходимо произвести расчет. Количество же участков разбиения зависит от свойств подынтегральной функции и выбирается намного больше, чем это необходимо для обеспечения заданной точности. Чтобы не делать лишних вычислений (а с ростом вычислений увеличивается и аппаратная ошибка, связанная с конечной длиной числа, представленного в ЭВМ), используют алгоритм с удвоением отрезков разбиения и сравнением интегралов, вычисленных с n отрезками разбиения и 2n. Алгоритм метода. 1. Вычисление интеграла с двумя отрезками разбиения. 2. Увеличение отрезков разбиения в 2 раза. 3. Вычисление интеграла с новым количеством отрезков. 4. Сравнение предыдущего и вычисленного значения интеграла. Если разность значений больше заданной точности, то перейти на шаг 2, иначе конец алгоритма. Если вычисление интеграла (шаг 3) производить по алгоритму, приведенному в работе № 4, то вычисление одних и тех же значений функции будет проводиться многократно, что не рационально. Желательно при вычислении интеграла с новым количеством отрезков использовать результаты предыдущих вычислений. Это достигается следующим образом.
Рис. 7. Вычисление интеграла с двухкратным увеличением количества отрезков разбиения. На рис. 7. представлена схема вычисления интеграла по приведенному выше алгоритму. Очевидно, что значения Пример. Найти значение интеграла
Рис. 8. Блок-схема алгоритма вычисления интеграла с заданной точностью. Варианты заданий приведены в табл.4, точность вычислений ЛАБОРАТОРНАЯ РАБОТА №6. Шаговые методы интегрирования дифференциальных уравнений первого порядка. Дано дифференциальное уравнение первого порядка Численные методы решения задачи Коши делятся на шаговые и разностные. К шаговым относятся методы Эйлера, Рунге-Кута, Гилла. К разностным - Адамса, Милна, Штермера, Гаусса и другие. Метод Адамса рассматривается в работе №7. 1. Метод Эйлера. Решение Задачи в конечном итоге сводится к интегрированию обыкновенного дифференциального уравнения
с начальным условием
Если принять
- рабочая формула метода Эйлера. Алгоритм метода. 1. Задаем h, начальные значения 2. Вычисляем 3. Изменяем i и x. 4. Если найдены все точки, то конец, иначе перейти к шагу 2. 2. Метод Эйлера-Коши. При интегрировании дифференциального уравнения (13) по формуле трапеций, получаем уравнение
Выражение Таким образом рабочие формулы метода Эйлера-Коши имеют вид:
Алгоритм метода Эйлера-Коши аналогичен алгоритму метода Эйлера. 3. Модифицированный метод Эйлера. В данном методе при интегрировании уравнения (13) применятся формула центральных прямоугольников:
Неивестная
Алгоритм аналогичен алгоритму метода Эйлера. 4. Метод Рунге-Кутта четвертого порядка. Из широкого класса методов типа Рунге-Кутта наиболее широко используется метод Рунге-Кутта четвертого порядка. При разложении
Решение ищется в виде где Итоговая рабочая формула:
Алгоритм аналогичен методу Эйлера. Варианты заданий приведены в таблицен 5. Задания 1, 4, 7, 10, 13, 16, 19, 22, 25, 28 выполняются методом Рунге-Кутта. Задания 2, 5, 8, 11, 14, 17, 20, 23, 26, 29 выполнять модифицированным методом Эйлера. Задания 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 выполнять методом Эйлера-Коши.
Таблица 5. Варианты заданий к лабораторной работе №6.
ЛАБОРАТОРНАЯ РАБОТА №7. Интегрирование дифференциального уравнения разностным методом Адамса. Введем сетку значений аргумента
и разностные методы, в которых очередное сеточное значение определяется по нескольким предыдущим
Формула разностного метода Адамса может быть получена, если проинтегрировать исходное дифференциальное уравнение на отрезке
Ограничиваясь полиномом третьего порядка и проведя интегрирование полинома, получим рабочую формулу, в которой значение конечных разностей заменены их выражениями через значения в узлах сетки
При использовании разностного метода Адамса проблемой является получение первых, так называемых "стартовых" точек, в нашем примере это Алгоритм метода. 1. Определяем стартовые точки 2. Вычисляем 3. Вычисляем новые значения сеточной функции
4. Если 5. Переприсваиваем
6. Перейти к шагу 3. Варианты заданий приведены в таблице 5. ЛАБОРАТОНАЯ РАБОТА № 8. Решение систем линейных алгебраических уравнений. Системой линейных алгебраических уравнений n-го порядка называется система
Решением этой системы является значение неизвестных
В дальнейшем предполагается, что это условие всегда выполнено. 1. Метод Гаусса (схема единственного деления). Идея метода Гаусса основана на последовательном исключении неизвестных и преобразовании системы (23) к специфическому виду (24) системы с треугольной матрицей (прямой метод хода).
После этого осуществляется последовательное определение неизвестных Метод Гаусса относится к группе так называемых "точных" методов, теоретически он позволяет с помощью конечного числа действий вычислить точный результат. Однако при практических расчетах возникают вычислительные погрешности, которые искажают результат тем сильнее, чем выше порядок системы. Условием сходимости метода является отличие от нуля определителя матрицы системы. При программировании метода и отладке программы целесообразно по окончании прямого хода вывести для на контроля на печать треугольную матрицу. В готовой программе этот оператор печати может быть удален.
Алгоритм метода. 1. Положить s=1 2. Для j=s+1,s+2,...,n положить 3. Положить 4. Положить i= s+1 5. Для j=s+1,s+2,...,n положить 6. Положить 7. Если 8. Положить s=s+1; если 9. Вычислить 10. Положить s=s-1 11. Вычислить 12. Если 2. Метод простой итерации. Идея метода состоит в том, чтобы задавшись некоторыми значениями неизвестных
Рабочая формула метода -
Условие сходимости метода Методы простой итерации относятся к группе "приближенных" методов. Это значит, что они дают за конечное число действий лишь приближенный результат, однако этот результат может удовлетворять пользователя своей точностью. Критерием сходимости методов является условие
При программировании метода полезно организовать выдачу на печать всех последовательных приближений; задавая значения коэффициентов Алгоритм метода. 1. Зададимся значениями 2. Для i=1,2,...,n вычислим значения 3. Найти величину - наибольшую из разностей 4. Если < ,то 5. Для i=1,2,...,n присвоить 6. Перейти к шагу 2.
Таблица 6. Варианты заданий к лабораторной работе №8.
Поиск по сайту: |
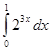
и 
постоянны для интеграла с любым количеством отрезков разбиения, поэтому их можно вычислить один раз в начале программы. Значения промежуточных результатов ( 
для двух отрезков разбиения) будут использоваться как четные слагаемые для следующего значения интеграла ( 
для четырех отрезков разбиения). Таким образом остается вычислить только сумму для нечетных значений функции.
методом Симпсона с точностью 
. Блок-схема алгоритма для данного примера приведена на рис.8.
с начальным условием 
. Необходимо вычислить сеточное представление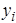 
частного решения y=y(x), удовлетворяющее дифференциальному уравнению и начальному условию.
(13)
(метод левых прямоугольников), то
(15)
(16)
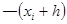из правой части находится по методу Эйлера (15).
(17)
(18)
находится также по методу Эйлера (15). Рабочие формулы модифицированного метода Эйлера:
(19)
в ряд Тейлора в окрестности точки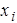 
до четвертого порядка малости получаем
(20)
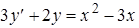
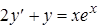
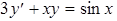
где h=const - шаг сетки, i=0,1,2,.... Сеточное представление частного решения 
. Для его определения существуют шаговые методы, в которых очередное сеточное значение определяется по данному:
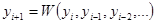
и подынтегральную функцию в правой части уравнения заменить интерполяционным полиномом Ньютона для интерполирования в конце таблицы.
(21)
(22)
. Они могут быть получены с помощью шаговых методов точности не ниже третьего порядка, например методом Рунге-Кутта четвертого порядка.
.
.
, то конец вычислений, в противном случае перейти к шагу 5.
.
(23)
. Коэффициенты матрицы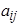 
и правые части 
предполагаются заданными. Условием существования и единственности системы (23) является неравенство нулю определителя матрицы
(24)
(обратный ход метода).
, перейти к шагу 5.
. перейти к шагу 2, в противном случае к шагу 9.
, перейти к шагу 10.
(начальным приближением), с помощью вычислительной процедуры получить "уточненные" значения неизвестных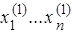 
. Это уточнение продолжается до тех пор, пока значения 
не будут вычислены с заданной точностью. Для применения метода система (23) долж на быть преобразована к виду:
(24)
(25)
.
, где 
-норма матрицы 
. Критерий окончания вычислительного процесса 
, где - заданная точность вычислений.
или значения правых частей 
.
.
для i=1,2,...,n.
при 
при 
при 