 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сызба геометриясыдегеніміз не?
Сызбанысызужолдарыдүниежүзіндегіелдердіңбарлығынабірдейортақболғандықтан, мектепқабырғасындаөтетінсызупәніхалықаралық, интернационалдық техника тіліболыптабылады. Себебісызбаныорындаукезіндеүлгіқалып (стандарт) бойыншабелгілітоғызсызықтүріқолданылады. ФранцуздыңатақтығалымыжәнемемлекетқайраткеріГаспар Монж (1746 – 1818) өзінедейінгікескіндерді салу туралымағлұматтардыжинақтапбелгілібіржүйегекелтіреотырып, олалғашрет 1795 жылы «Сызба геометрия» аттыеңбегінжазыпшықты. Міне осы уақыттанбастапсызба геометрия жекеғылымретіндеқалыптасабастады. Жоғарыдаайтыпкеткендей, егерсызба техника тіліболса, ондасызба геометрия осы тілдіңграмматикасыболыптабылады [7, 8, 11]. БіздіңдәуірімізгедейінөмірсүргенЭсхилдің (б.д.д. 525-456 ж.ж.), Анаксагордың (б.д.д. 500-428 ж.ж.), Демокриттің (б.д.д. 460-380 ж.ж.), Евклидтың (б.д.д. III ғасыр) жәнеВитрувийдің (б.д.д. I ғасыр) еңбектеріндесызба геометрия негіздеріболған.Бұлсаланыңғылымретіндеқалыптасуына орта ғасырдаөмірсүргенбабаларымызӘл Хорезми (780-850), ӘлФараби (870-950), Әл Бируни (973-1050), НасрединТусидіңеңбектері мен зерттеулеріұшантеңіз. Қайтаөрлеузаманындаөмірсүрген Леонардо да Винчидің (1455-1519), Декарттың (1596-1650) жәнеДезаргтың (1593-1662) жасағантеорияларысызбагеометрияныңжекеғылымболыпжетілуінесебепкерболған. Сызба геометрия пәнісызбанықалайоңайжәнетүсініктісалуға, сызбанысызудыңәдістері, сызбанықалайоқуға, сызбаәдістерінпайдаланаотырып, қандайесептершығаруғаболатыныт.б. секілдісұрақтар мен мәселелердіңшешілужолдарынқарастырады. Соныменқатарсызба геометрия сызбаны салу мен олтуралыбілімдіжәнесызбалардыңкөмегіменинженерлікесептердішешутеориясынмеңгертетінпәнболыпсаналады [1, 2, 3]. Сызба геометрия төмендегідейбөлімдердентұрады: проекциялауәдістері; аксонометриялықпроекциялар; нүкте мен түзусызықпроекциялары; қисықсызық пен жазықтықпроекциялары; беттерпроекциялары; тұрғылықты (позициялық) жәнеөлшем (метрикалық) есептері; сызбанытүрлендірутәсілдері; көлеңкелер. Осы бөлімдердітолықмеңгерген студент өзініңойлауқабілетінөрістетеотырып, кеңістіктеорналасқаннәрселердіңкескіндерін салу, сызбадағыкескіндерарқылыжаңабірнәрсеніқұрастыружәнесызбадағытүрліесептердішығарумәселелерінен мол мағлұматалады. Қазіргіинженерлік графика пәніжоғарыдааталғансызба геометрия пәні мен машина жасаужәнеқұрылыссызбаларыныңтеорияларынзерттейтінғылым. Инженерлік графика теорияларыныңжетістіктері техника мен ғылымныңәртүрлісалаларындакеңіненқолдануда. Сондықтанжержұмыстарыныңсызбаларынсауаттыорындау, инженерлікғимараттардыжобалаужәнетұрғызуүшін, аса қажеттіжербетіндесалынатынғимараттардысызбаменкескендеутеориясыныңнегіздерін инженер осы инженерлік графика теориясыарқылыбіліпүйренеді [9, 10 12, 13]. 2. Проекциялау тәсілдері Проекциялау әдістері өзінің кескінделу жолдарына байланысты екі түрге бөлінеді: орталық(центрлік) және параллель проекция әдістері. Төменде осы проекциялау әдістерінің пайда болу жолдарын қарастырамыз. Орталық проекция әдісі.Кеңістікте орналасқан кескіндеу жазықтығы П0 мен кескіндеу орталығы S нүктесін және кеңістікте орналасқан геометриялық фигураларды алып, орталықтан проекциялау әдісін салуға болады (39- сурет). Мысал ретінде кеңіс-тікте орналасқан АВ кесін-дісі мен кескінделуші П0 жазықтығын және кескіндеу S нүктесін алайық. Осы S кескіндеу нүктесінен кеңіс-тікте орналасқан АВ кесін-дісінің А және В төбелері арқылы өтетін кескінделуші сәулелер жібереміз. 39-суретте көрсетілгендей бұл сәулелер (s) кескінделуші П0 жазықтығын А0 және В0 нүктелерінде қиып өтеді. Осы А0 және В0 нүктелерін өзара қоссақ, біз кеңістіктегі АВ кесіндісінің кескінделуші П0 жазықтығындағы бір нүктеден (орталықтан) шыққан проекциясын табамыз. Сонымен, егер кескінделуші сәулелер бір нүктеден шыққан немесе тараған болса, онда мұндай проекция тәсілін бір нүктеден немесе орталықтан (центрлік) проекциялау әдісі дейді. Параллель проекциялау әдісін салу үшін келесі мысалды қарастырайық. Кеңістікте орналасқан АВ кесіндісі мен кескінделуші П0 жазықтығы берілсін. Осы кеңістікте орналасқан АВ кесіндісінің А және В төбелері арқылы өзара параллель өтетін кескінделуші сәулелер жүргізейік. Бұл сәулелер кескінделуші П0 жазықтығын екі (А0 және В0) нүктеде қиып өтеді. Осы А0 және В0 нүктелерін өзара қоссақ, онда біз кеңістікте орналасқан АВ кесіндісінің кескінделуші П0 жазықтығындағы проекциясын табамыз. Егер кескінделуші сәулелер (s) өзара параллель болса, онда мұндай проекция әдісін параллель проекциялау әдісі дейді (40-сурет). Параллель проекциялау әдісі кескінделуші П0 жазықтығына сәулелердің кескінделулеріне бай-ланысты екі түрге бөлінеді. Егер П0 жазықтығына сәулелер сүйір немесе доғал бұрышпен кескінделсе, онда параллель проекциялау әдісін қиғаш бұрышты параллель проекциялау әдісі дейді (40-сурет). Ал сәулелер П0 жазықтығына тік бұрышпен кескінделсе, онда параллель проекциялау әдісін тікбұрышты параллель проек-циялау әдісі дейді (41-сурет). Тікбұрышты параллель проек-циялау әдісінің дербес түрі сандық белгілері бар проекциялар әдісі (42-сурет). Егер кеңістікте орналасқан нәрсенің (заттың) горизонталь (көлденең) немесе нольдік деңгейлі жазықтығына П0 тікбұрышты проекциялау әдісімен кескінделген кескіні сан арқылы белгіленген болса, онда кескінделу әдісі сандық белгілері бар проекциялар деп аталады. Бұл проекциялау әдісінде горизонталь (көлденең) немесе нольдік деңгейлі жазықтығында П0 орналасқан геометриялық элементтің кескінінің жанына оның осы жазықтық пен кеңістікте орналасқан элементтің ара қашықтығын, яғни оның биіктігін көрсететін санды жазып қояды. Мысал ретінде 42-суретте көрсетілгендей кеңістікте орналасқан АВ кесіндісін аламыз. Кесіндінің А және В төбелерінен көлденең П0 проекция жазықтығына перпенди-куляр сәулелер түсіреміз. Осы сәулелер көлденең П0 проекция жазықтығын қиып өтеді. Табылған нүктелерді латынның бас әрпімен белгілеп, әріптердің астыңғы жағына сан арқылы осы қиылысқан нүктелер мен түзу төбелерінің ара қашықтығын жазып қояды. Егер табылған қиылысу нүктелерін өзара қоссақ, онда кеңістікте орналасқан АВ түзу сызығының көлденең П0 проекция жазықтығындағы сандық белгілері бар проекциясы болады. 3. Нүкте мен түзү сызықтың кешенді сызбасы. Кеңістікте нүкте мен түзу сызық әр түрлі жағдайда кездесуі мүмкін. Кеңістікте орналасқан нүкте түзу сызық бойында орналасуы немесе түзу сызықтан тыс орналасуы мүмкін. Енді осы тақырыпқа мысал ретінде 87-суреттегі нүктелер мен түзудің өзара орналасуларын қарастырайық. Суретте С және D нүктелері мен АВ түзу сызығының горизонталь және фронталь проекция жазықтығындағы эпюрасы берілген. Кеңістікте орналасқан D нүктесі АВ түзу сызығының горизонталь және фронталь проекция жазықтықтарындағы кескіндерінің бойында жатқан нүкте, яғни D нүктесі АВ түзу сызығына тиісті немесе түзу бойында орналасқан нүкте. Ал енді С нүктесін қарастыратын болсақ, онда С нүктесінің фронталь проекциясы С2 нүктесі АВ түзу сызығының фронталь проекция жазық-тығындағы кескін бойында емес тысқары орналасып жатыр. С нүктесінің горизонталь проекциясы С1 нүктесі АВ түзу сызығының горизонталь проекция жазықтығындағы кескін бойында жатыр, яғни кеңістікте орналасқан С нүктесі АВ түзу сызығының сыртында тыс орналасқан түзу бойында жатпайтын нүкте. Егер нүкте кескіні түзу проекциясының бойында жатса, онда нүкте түзуге тиісті немесе бойында жатады. 4. Дербес және жалпы жағдайдағы түзүлер. Жалпы жағдайдағы орналасқан тузулер. 65-суреттің жоғарғы жағында түзу сызықтың кеңістіктегі жалпы жағдайда орналасқан АВ түзу сызығы қара түсті сызықпен берілген. Осы кеңістіктегі түзу сызықтың А және В төбелерінен бірінші П1 горизонталь проекция жазықтығына екінші П2 фронталь проекция жазықтығына перпенди-куляр сәулелер жүргіземіз. Бұл сәулелер проекция жазықтықтарымен қиылысып, А1В1 және А2В2 нүктелерін береді. Егер осы табылған нүктелерді өзара қоссақ, онда кеңістікте орналасқан жалпы жағдайдағы түзу сызықтың горизонталь және фронталь проекция жазықтығындағы проекциясын табамыз. Бұл табылған проекциялар қызыл түсті түзу сызықпен көрсетілген. Осы мысалдан жалпы жағдайда орналасқан АВ түзу сызығының көлденең П1 горизонталь проекция жазықтығы мен П2 фронталь проекция жазықтығына жасайтын бұрыштық шамасын α және
Дербес жағдайда орналасқан тузулер. Кеңістіктегі түзу сызықтар өздерінің проекция жазықтықтарына орналасуларына байланысты екі түрге бөлінеді: параллель және проекциялаушы түзулер. Егер кеңістікте орналасқан түзу сызықтың кескіні П1 горизонталь проекция жазықтығына, П2 фронталь проекция жазықтығына және П3 профиль проекция жазықтығына параллель немесе перпендикуляр орналасса, онда мұндай түзулерді дербес жағдайда орналасқан түзулер дейміз.
Ал 67-суретте кеңістікте орналасқан дербес жағдайдағы параллель түзу сызықтың П1 горизонталь проекция жазықтығымен П2 фронталь проекция жазықтығындағы проекциясы көрсетілген.
Енді дербес жағдайда орналасқан проекциялаушы түзуді қарастырайық (68-сурет). Егер дербес жағдайда орналасқан түзу сызық П1 проекция жазықтығына перпендикуляр (тікше) орналасса, яғни түзудің П1 горизонтальпроекция жазықтығындағы проекциялары бір нүктеде беттескен бір ғана нүкте болса, онда мұндай түзу сызықты горизонталь проекциялаушы түзу сызық дейді.
Ал 69-суретте кеңістікте орналасқан түзу сызықтың эпюрасы, яғни түзудің көлбеу П1 проекция жазықтығындағы кескіні мен П2 проекция жазықтығындағы проекциясы көрсетілген. Дербес жағдайда орналасқан горизонталь проекциялаушы түзу сызық П1 проекция жазықтығына перпендикуляр орналасқандықтан, түзу сызықтың П2 проекция жазықтықтағы кескіні шын ұзындығымен кескінделеді. Түзу сызықтың П2 проекция жазықтығындағы кескіні түзудің нақты шамасы болады, ол сызық қызыл түспен сызылған, өйткені түзу сызық П2 фронталь проекция жазықтығына параллель орналасқан.
5. Түзү сызықтың ізі Түзу сызықтың іздері деп кеңістікте орналасқан түзу сызықтың проекция жазықтықтарымен қиылысу нүктелерін айтады. Бізде үш проекция жазықтықтары болғандықтан, түзу сызықтың үш ізі болады. Түзу сызықтың П1 горизонталь проекция жазықтығындағы ізін латынның үлкен М әрпімен белгілейміз. Ал түзу сызықтың П2 фронталь проекция жазықтығындағы ізін латынның үлкен N әрпімен, ал П3 профиль проекция жазықтығындағы ізін Р әрпімен белгілейміз. Енді кеңістікте орналасқан жалпы жағдайдағы түзу сызықтың проекция жазықтықтарындағы іздерін салуға мысал қарастырайық (70-сурет). Ол үшін бірінші октантта жалпы жағдайда орналасқан АВ түзу сызығын алайық. Егер жалпы жағдайда орналасқан түзу сызықты бастапқы нүктесінен соңғы нүктесіне қарай немесе керісінше соңғы нүктесінен бастапқы нүктесіне қарай өз бағытымен проекция жазықтықтарына дейін созып қиылыстырсақ, онда біз үш проекция жазық-тықтарында түзудің қиы-лысу нүктелерін табамыз (70-сурет). Түзу сызықтың А нүктесінен В нүктесіне қарай s бағытымен көлденең П1 проекция жазықтығына дейін соза-мыз. Бұл созылған түзу сызық П1 горизонталь проекция жазықтығын М1 нүктесінде қиып өтеді. Осы қиылысу нүктесі түзудің П1 жазықтығындағы ізі болып табылады. Егер АВ түзуін әрі қарай созсақ, онда түзу сызықтың П2 фронталь проекция жазықтығындағы ізі N2 нүктесін табамыз. Ал егер түзу сызықтың В нүктесінен А нүктесіне қарай s бағытымен профиль П3 проекция жазықтығына дейін созсақ, онда созылған түзу сызық П3 проекция жазықтығына Р3 нүктесінде қиып өтеді. Бұл қиылысу нүктесі түзу сызықтың П3 профиль проекция жазықтығындағы ізі болып табылады. Төмендегі 71-суретте кеңістіктегі жалпы жағдайда орналасқан түзу сызықтың үш проекция жазықтықтарындағы іздерін эпюрде көрсетеміз. Алдымен түзу сызықтың үш проекция жазықтықтарындағы проекциясын анықтап аламыз. Содан соң түзу сызықтың А нүктесінен В нүктесіне қарай s бағытымен П1 және П2 проекция жазықтықтарына дейін созамыз. Бұл созылған түзу сызық П1 горизонталь проекция жазықтығын М1 нүктесінде, ал П2 фронталь проекция жазықтығын N2 нүктесінде қиып өтеді. Енді түзу сызықтың В нүктесінен А нүктесіне қарай s бағытымен П3 проекция жазықтығына дейін созамыз. Созылған түзу сызық П3 профиль проекция жазықтығын Р3 нүктесінде қиып өтеді. Енді кеңістіктегі жалпы жағдайда орналасқан тағы бір түзу сызықтың екі проекция жазықтықтарындағы іздерінің эпюрін табуға мысал қарастырайық (72-сурет). Суретте көрсетілгендей жалпы жағдайда орналасқан АВ түзу сызығын аламыз. Алдымен, А2В2 түзу сызығының П2 проекция жазықтығындағы проек-циясын А нүктесінен В нүктесіне қарай s бағытымен х осіне дейін созып, М2 нүктесін белгілеп аламыз. Содан кейін П1 проекция жазықтығындағы А1В1 түзу сызығының проекциясын В нүктесінен А нүктесіне қарай s бағытымен х осіне дейін созып, N1 нүктесін анықтап, сәуле жүргіземіз. N1 және М2 нүктелерінен жүргізген сәулелер А1В1 және А2В2 проекцияларының созындысымен N2 және М1 нүктелерінде қиылысады. Бұл табылған нүктелер кеңістікте орналасқан жалпы жағдайдағы АВ түзу сызығының П1 және П2 проекция жазықтығындағы горизонталь және фронталь іздері болады. 6-7-8. Аксонометрия.Аксонометрия проекция жазықтығындағы бір нүктеден өтетін кез келген үш түзу сызық тікбұрышты координаталар жүйесінің проекциясы болады. Мысал ретінде кеңістікте орналасқан кез келген бір А нүктеcін алайық (43-сурет). Бұл нүкте тік бұрышты координаталар жүйесінде орналасқан. Параллель проекциялау әдісі бойынша s бағытымен А нүктесі мен тік бұрышты декарттық координаталар жүйесі аксонометриялық проекция (П/) жазықтығына кескінделеді. Осы (П/) проекция жазықтығындағы А/ нүктесі кеңістікте орналасқан А нүктесінің аксонометриялық проекциясы болады. Аксонометрия проекциясының масштабын анықтау үшін кеңістікте орналасқан тікбұрышты координаталар жүйесіне (Охуz) координаталар жүйесінің бас нүктесінен үш (ех, еу, еz)кесінділерін саламыз (43-сурет). Осы кесінділердің аксонометриялық проекциялары (
Егер бұрмалану көрсет-кіштері барлық осьтерде өзара тең ( Егер бұрмалау көрсет-кіштері екі осьте ғана өзара тең ( Егер бұрмалау көрсеткіштері барлық осьтерде әр түрлі ( Аксонометрия проекцияларын проекциялау бағыттарына қарай екі топқа бөлінеді. Егер проекция жазықтығына проекциялау бағыты тік бұрышпен (s=900) бағытталса, онда аксонометриялық проекция тікбұрышты аксонометрия деп аталады. Ал егер проекция жазықтығына проекциялау бағыты сүйір немесе доғал бұрышпен (s Проекциялау бағыттары мен бұрмалану көрсеткіштері өзара байланысты, бұл тұжырым төмендегі формуламен дәлелдеуге болады
Егер проекциялау бағыты тікбұрышты болса, яғни осы формуладағы
Жалпы бұрмалану көрсеткіштерінің мәні жуық шамамен бүтін сан ретінде беріледі. Әр аксонометриялық проекция үшін бұл сандар әр түрлі болады. Олардың мәндерін төменгі бөліктерде қарастырамыз. Аксонометриялық проекциялардың стандартты түрлері Аксонометриялық проекцияларға қойылатын негізгі талаптардың бірі -нәрсенің кескінін салу оңай және мейлінше аз бұрмалануы. Осы талаптарды қанағаттандыру мақсатында халықаралық стандарттар ұйымы бес түрлі аксонометриялық проекциялар түрін тағайындаған. Бұл стандарт аксонометриялардың атаулары: тікбұрышты изометрия; тікбұрышты диметрия; қиғаш бұрышты фронталь изометрия; қиғаш бұрышты фронталь диметрия және қиғаш бұрышты горизонталь изометрия. Тікбұрышты изометрия Аксонометриялық проекциялау әдісінің ішіндегі ең оңай және қарапайым түрі тікбұрышты изометрия болып табылады. Тікбұрышты изометрияда барлық координата осьтерінің аксонометриялық проекциялау жазықтығына құлау бұрыштары бірдей және барлық осьтердегі бұрмалану көрсеткіштері өзара тең болады. Енді осы бұрмалану көрсеткішінің сандық мәнін қарастырайық. Ол үшін жоғарыда қарастырылған тікбұрышты бұрмалану көрсеткіштерінің (2) формуласын аламыз. Барлық координата осьтерінде мәндер өзара тең болғандықтан 2-формуланың оң жағы былай болып өзгереді:
Енді тікбұрышты изометрия проекциясының координаталар осьтерінің арасындағы бұрыштық шамаларын 44-суретте көрсетілгендей, жазықтықтың үшбұрышты іздері арқылы қарастырайық.
Жоғарыда қарастырылған бұрмалану көрсеткіші тек осьтер бойындағы шамалар мен осьтерге параллель болатын сызықтар үшін ғана қолданылады. Шеңбердің тікбұрышты изометриясы Енді шеңбердің аксонометриялық проекциясы тікбұрышты изометриясынсалу жолын көрсетелік. Шеңбердің аксонометриялық проекциясы эллипс болғандықтан, үлкен және кіші осьтер болады (46-сурет). 46-суретте эллипстің үлкен осьтері аксонометриялық осьтерге перпендикуляр болады. Ал кіші осьтер сол осьтерге бағыттасып немесе беттесіп жатады. Эллипстің үлкен осінің бұрмалану көрсеткішін табу үшін, 1 санын осьтердің бұрмалану көрсеткішіне бөлеміз (
Бір айтып кететін жайт, сфераның тікбұрышты изомет-риясы сфераның диаметрінен 1.22 есе үлкен болады, себебі эллипстің үлкен осінің ұзындығын анықтау үшін бұрмалану көрсеткішіне көбей-теміз (
Тікбұрышты диметрия Аксонометриялық проекциялау әдісінің тағы бір түрі тікбұрышты диметрия. Тікбұрышты диметрия көбінде табаны дөңгелек конусты беттер мен тең табанды алты немесе бес жақты призма және пирамиданың аксонометриялық проекциясын салғанда өте ыңғайлы. Оның себебі тікбұрышты изометрияда жоғарыда айтылған беттердің айналу осьтері аксонометрия осімен беттесіп, беттердің көріктігі бұрмаланып кетеді. Сондықтан екі аксонометриялық осьтердегі бұрмалану көрсеткіштері өзара тең, ал үшінші осьтегі бұрмалану көрсеткіші екі есе кіші. Енді осы айтылған бұрмалану көрсеткіштерінің сандық мәндерін қарастырайық. Ол үшін жоғарыдағы қарастырған тікбұрышты бұрмалану көрсеткіштерінің (2) формуласын алып, у осінің бойындағы бұрмалану көрсеткішін r орнына қойып формуланы қайта жазамыз
Егер х және z осьтерінің бұрмалану көрсеткіштері жуық шамамен 0,94-ке тең болса, онда у осіндегі көрсеткіш екі есеге кем болғанда шамамен 0,47-ге тең болады.
Егер екі X/ және Z/ аксонометриялық осьтерінде бұрмалану көрсеткіштері өзара тең болса, онда кеңістіктегі координаталар осінің бойындағы кесінді мен аксономериялық координаталар осінің бойындағы кесінділердің қатынастары да өзара тең болады (47-сурет). Олай болса кеңістікте орналасқан [ОХ/] және [ОZ/] кесінділерінің ұзындығы 1-ге тең болады. Ал аксонометрия жазықтықта орна-ласқан [О/Х/] және [О/Z/] кесінділердің ұзындығы
Шеңбердің тікбұрышты диметриясы
Шеңбердің аксономет-риясы эллипс болғандықтан, оның үлкен және кіші осьтері болады. Егер 49-суретке зейін қойып қарасаңыздар, эллипс-тің үлкен осьтері аксонометриялық осьтерге перпендикуляр, ал кіші осьтері аксонометриялық осьтерге параллель орналасқан. Эллипстің үлкен осінің бұрмалану көрсеткіші барлық жазықтықтарда немесе эллипстің үш көрінісінде 1.06-ға тең болады. Ал кіші осінің бұрмалану көрсеткіші горизонталь және профиль (қаптал) жазықтықтарында 0.35-ке тең болса, ал фронталь жазықтығында ол көрсеткіш 0.94-ке тең. Сфераның тікбұрышты изометриясы сфераның диаметрінен 1.06 есе үлкен болады, себебі эллипстің үлкен осінің бұрмалану көрсеткіші 1.06-ға тең. Қиғаш бұрышты фронталь изометрия мен диметрия
Қиғаш бұрышты горизонталь изометрия
Сондықтан бұл жағдайда аксонометриялық проекциялар кеңістікте орналасқан Қиғаш бұрышты горизонталь изометрия проекцияларында шеңбердің проекциясы горизонталь жазықтығында шеңбер болып, ал фронталь және профиль жазықтықтарында ол эллипс болып кескінделеді. Қиғаш бұрышты горизонталь изометрияда эллипстің үлкен және кіші осьтері ромбтардың диагональдарына беттесіп келеді. Эллипстің үлкен осінің бұрмалану көрсеткіші 1.37-ге және 1.22-ге тең болса, ал кіші осінің бұрмалану көрсеткіші 0.37-ге және 0.71-ге тең болады. 52-суреттегі сары жазықтықтағы эллипс шеңбердің алдынан қарағандағы, ал жасыл жазықтықтағы эллипс - шеңбердің оң жағынан қарағандағы көрінісі. Ал қоңыр жазықтықтағы көрінісі - шеңбердің горизонталь проекция жазықтығындағы көрінісі. Шеңбердің изометриялық проекциясын салу
Егер бұл табылған 7, 8, 9 және 10 нүктелерін өзара түйіндестіріп қоссақ, онда шеңбердің изометриясы эллипс болып табылады. Шеңбердің диметриялық проекциясын салу
Ескерту, бұл табылған эллипс шеңбердің жанынан және үстінен қараған көрінісі болады. Енді диметриядағы шең-бердің алдынан қарағандағы кескінін салып көрсетеміз. Ол үшін х және z осьтерін жүргізіп, О нүктесін анықтап аламыз. Осьтер бойына шеңбердің 9. Жазықтықтардың прокциялары. Егер бір түзудің бойында жатпайтын үш нүкте берілсе, онда осы нүктелер арқылы бір жазықтық жүргізуге болады, яғни жазықтық үш нүкте арқылы беріледі. Егер өзара қиылысқан немесе өзара параллель екі түзу сызықтар берілсе, онда осы түзулер арқылы бір жазықтық жүргізуге болады,яғни жазықтық өзара қиылысқан немесе өзара параллель екі түзу сызықтар арқылы беріледі. Егер түзу сызық пен сол түзу бойында жатпайтын нүкте берілсе, онда осы түзу мен нүкте арқылы бір жазықтық жүргізуге болады, яғни жазықтық түзу сызық пен осы түзу бойында жатпайтын нүкте арқылы беріледі. Сызбада жазықтықтар әр түрлі геометриялық фигуралар арқылы да беріледі (көбінесе үшбұрыш, төртбұрыш, бесбұрыш, алтыбұрыш, трапеция, параллелограмм, т.с.с. ). Сонымен қатар жазықтықтар проекция жазықтығындағы ізі арқылы да беріледі. Жазықтықты сандық белгілері бар проекцияларда екі әдіспен анықтауға болады: көлбеулік масштабпен және геометриялық элементтермен (үшбұрышпен, төртбұрышпен, және т.б.с.с.). 10.Жалпы және дербес жағдайдағы жазықтықтар.
Мысал ретінде алдымызда көрсетілген 73 және 74-суреттерді алатын болсақ, 73-суретте кеңістіктегі орналасқан жалпы жағдайдағы жазықтық үшбұрыш арқылы берілген. Бұл АВС үшбұрышты екі проекция жазықтықтарына параллель де, перпендикуляр да емес, яғни бұл жазықтық көлденең П1 және П2 фронталь проекция жазықтықтарындағы проекциялары әр түрлі үшбұрыштар. Ал 74-суретте жалпы жағдайда орналасқан жазықтықтың эпюрасы берілген. Жалпы жағдайда орналасқан жазықтықтың эпюрасын салу үшін үшбұрыштың төбелері А, В және С нүктелерін координаталар арқылы салып алып, араларын өзара қосамыз.
Дербес жағдайда орналасқан жазықтықтар Дербес жағдайда орналасқан жазықтықтар үш проекция жазықтығына орналасуына байланысты параллель немесе перпендикуляр болып екіге бөлінеді. Параллель және перпендикуляр дербес жағдайда орналасқан жазықтықтар өзара үшке бөлінеді, себебі бізде горизонталь, фронталь және профиль проекция жазықтықтары бар. Енді төменде осы аталған дербес жағдайда орналасқан жазықтықтардың кейбір түріне мысалдар келтіреміз.
Егер берілген жазықтықтың фронталь проекциясы бір ғана сызық және х осіне параллель орналасса, онда кеңістіктегі орналасқан жазықтық горизонталь (көлденең) проекция жазықтығына параллель орналасқан болады. Жазықтықтың горизонталь проекциясы нақты шамасымен проекцияланады. Енді жазықтықтың дербес жағдайда орналасқан перпендикуляр жазықтықтарға мысал қарастырайық (77-сурет). 77-суретте сары П1 горизонталь проекция жазықтығына кеңістікте орналасқан перпендикуляр АВС жазықтығының кеңістіктегі кескіні көрсетілген. Егер кеңістікте орналасқан АВС жазықтығының бар-лық төбелерінен көлденең П1 фронталь проекция жазықтығына перпенди-куляр сәулелер түсіргенде, П1 фронталь проекция жазықтығындағы кескіні түзу сызық болса, онда кеңістікте орналасқан дербес жағдайдағы жазықтық горизонталь проекция жазықтығына перпендикуляр жазықтық болады.
Егер дербес жағдайда орналасқан кеңістіктегі жазықтық проекциясы көлденең П1 горизонталь проекция жазықтығында түзу сызық ретінде кескінделсе, ал П2 фронталь проекция жазықтығындағы проекциясы үшбұрыш болып кескінделсе, онда кеңістікте орналасқан АВС жазықтығы көлденең П1 горизонталь проекция жазықтығына перпендикуляр орналасқан жазықтық болады. 78-суреттің горизонталь проекция жазықтығында АВС жазықтығының проекциясы бір ғана түзу сызық болып кескінделген, яғни жазықтықтың үш төбесі бір түзуге проекцияланып тұр. Ал П2 фронталь проекция жазықтығындағы проекциясы үшбұрыш болып кескінделеді. Ескерту, бұл П2 фронталь проекция жазықтығындағы АВС жазықтығының проекциясы үшбұрыш нақты шамасымен проекцияланбаған, себебі бұл жазықтық фронталь проекция жазықтығына параллель емес. 11. 12. Жазықтықтың іздері. Енді жалпы жағдайда орналасқан жазықтыққа мысал қарастырайық (81-сурет). 81-суретте П1және П2 проекцияжазықтықтары берілген. Р жазықтығы П1
Поиск по сайту: |
Егер кеңістікте орналасқан түзу сызық горизонталь, фронталь және профиль проекция жазықтықтарына параллель немесе пердендикуляр болмаса және осы жазық-тықтардың бойында жатпаса, онда мұндай түзуді жалпы жағдайда орналасқан түзу сызық дейді (65-сурет). Жалпы жағдайда орналасқан түзу сызық кескіні проекция жазықтықтарына өз шын ұзындығымен (нақты шамасымен) кескінделмейтінін анықтаймыз.
бұрыштарын көрсетеміз (65-сурет).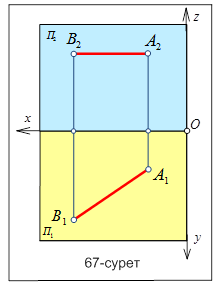
Егер кеңістікте орналасқан түзу П1 горизонталь проекция жазық-тығындағы кескініне немесе түзу сызықтың П2 фронталь проекция жазықтығындағы кескіні х осіне параллель орналасса, онда мұндай дербес жағдайда орналасқан түзулерді параллель түзулер дейді (66-сурет). Мысал қарастыратын болсақ, онда 66-суретте параллель орналасқан түзу сызықтың кеңістікте орналасқан кескіні көрсетілген.
Дербес жағдайда орналасқан параллель түзу сызық проекциясы П1 жазықтығына параллель орналасқандықтан, түзудің жазықтықтағы кескіні нақты шамасымен кескінделеді, яғни түзу сызықтың П1 проекция жазықтығындағы кескіні түзудің шын ұзындығы (нақты шамасы) болады.
68-суретте горизонталь проекциялаушы түзу сызықтың кеңістікте орналасқан кескіні көрсетілген. Суретте түзу сызықтың кеңістіктегі орналасуын қара сызықпен көрсетсек, фронталь проекция жазықтығындағы кескінін қызыл түсті сызықпен көрсетілген.
, 
, 
) аксонометрия масштабы деп аталады. Бұл кесінділердің айырмашылығы аксонометрия проекцияларының бұрмалану көрсеткіштері болады. Бұрмалану көрсеткіштері әр координата осінде әр түрлі болуы мүмкін. Аксонометрия проекциясындағы абсцисса осі бойындағы бұрмалану көрсеткішін латынның p әрпімен белгілейміз ( 
). Ал ордината осі бойындағы бұрмалану көрсеткішін латынның q әрпімен белгілейміз ( 
). Аксонометриядағы аппликата осінің бұрмалану көрсеткішін латынның r әрпімен белгілейміз ( 
).
Бұрмалану көрсеткіш-теріне байланысты аксоно-метриялық проекциялар үш түрге бөлінеді.
) болса, онда мұндай аксонометрия-лық проекцияны изометрия деп атайды. Изометрияны ежелгі грек тілінен аудар-ғанда «тең өлшем» деген мағынаны береді.
) болса, онда мұндай аксонометриялық проекцияны диметрия дейді. Аудармасы «екі өлшемге» тең деген мағына береді.
) болса, мұндай аксонометриялық проекция триметрия деп аталады.
900) бағытталса, онда аксонометриялық проекция қиғаш бұрышты аксонометрия деп атайды.
. (1)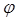
мәні 900 бұрыш болса, онда формула
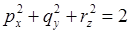(2) осындай түрге өзгереді.
. (3) Егер бұл 3-формуланы әрі қарай шешсек, онда координаталардағы осьтердің мәндері төмендегідей болады: 
(4) Бұл бұрмалану көрсеткіштерін тікбұрышты изометрияда қолдануға оңай болу үшін жуық шамамен 1-ге тең деп аламыз.
Егер кеңістіктегі координаталар осінің бойындағы кесінді мен аксонометриялық координаталар осінің бойындағы кесінділердің қатынастары өзара тең болса, онда бұрмалану көрсеткіштері де өзара тең болады (44-сурет). Бұл дегеніміз 
Х/О/Y/, 
). Сонда эллипстің үлкен осінің бұрмалану көрсеткіші 1.22-ге тең болады. Ал кіші осьтің бұрмалану көрсеткіші 0.7-ге тең.
46-суретте қоңыр жазық-тықтағы эллипс, бұл шеңбердің үстінен қарағандағы горизонталь проекция жазықтығындағы көрі-ніс берілген. Ал сары жазық-тықтағы эллипс – шеңбердің алдынан қарағандағы фронталь проекция жазықтығындағы кө-рінісі. Жасыл жазықтықтағы эллипс - шеңбердің оң жағынан қарағандағы көрінісі болып табылады.
).
. (5) Егер бұл формуланы әрі қарай шешетін болсақ, онда х және z координаталардағы осьтердің мәндері төмендегідей болады: 
. (6)
Енді тікбұрышты диметрия координаталар осьтерінің арасындағы бұрыштық шамаларын 47-суретте көрсетілгендей жазықтықтың үшбұрышты іздері арқылы қарастырайық.
тең болады. Тікбұрышты үшбұрыш 
тең. Суреттегі 
) шамасын анықтаймыз. Ол үшін екіге бөлінген тікбұрышты үшбұрыштың 
) мен [О/Z/] кесіндісінің ұзындығын ( 
) бөлеміз:
(7) онда 
. Сонымен О/Х/ және О/Z/ аксонометрия осьтердің арасындағы бұрыштық шама 97010/ градусқа тең болады. Ал О/Y/ және О/Z/ аксонометрия осьтердің арасындағы бұрыштық шама төмендегі формуламен табылады
(8) 48-суретте тікбұрыш-ты диметрияда аксономет-риялық осьтерді салу жолы көрсетілген. Бірінші жолы 
осінің бұрыштық шама-сын табу үшін 1/8 бөлікке, ал 
осінің бұрыштық шамасын 7/8 бөлікке бөлу арқылы болса, екінші жолы транспортирдің көмегімен жоғарыда табылған бұрыш-тық шамаларды қою арқылы жүзеге асады.
Енді шеңбердің тікбұрышты диметриядағы аксонометриялық проекциясын салу жолын қарастырайық (49-сурет). Суреттегі қоңыр жазықтықтағы эллипс бұл шеңбердің үстінен қарағандағы горизонталь проекция жазықтығындағы көрінісі, ал сары жазық-тықтағы эллипс, бұл шеңбер-дің алдынан қарағандағы фронталь проекция жазық-тығындағы көрінісі. Жасыл жазықтықтағы эллипс – шеңбердің оң жағынан қара-ғандағы профиль проекция жазықтығындағы көрінісі.
Егер сызбада фронталь проекция жазықтығында қисық сызықтар мен шеңберлер көбейіп кеткен болса, онда нәрсенің аксонометриясын салу үшін қиғаш бұрышты фронтальды изометрия мен диметрия пайдаланылады (50 және 51-суреттер). Бұл жағдайда аксоно-метриялық проекциялар кеңістікте орналасқан 
және 
координаталар жазықтығына парал-лель орналасады. 
және 
аксонометриялық осьтердегі бұрма-лану көрсеткіштері 1-ге тең болып, араларындағы бұрыштары 900 градус болады, яғни нәрсенің фронталь проекция жазықтығын-дағы проекциясы бұрмаланбай сол күйінде кескінделеді. Ал 
аксонометриялық осьтерінің арасындағы бұрыштық шама қиғаш бұрышты фронталь изометрия мен диметрия үшін 450 градус болады. Фронталь изометрия үшін бұрмалану көрсеткіші 1-ге тең (50-сурет), ал фронталь диметрия үшін – 0.5-ке тең болады (51-сурет). Қиғаш бұрышты фронталь изометрия мен диметрия проекцияларында шеңбердің проекциясы фронталь жазықтығында шеңбер болып, ал горизонталь және профиль жазықтықтарында ол эллипс болып кескінделеді. Қиғаш бұрышты фронталь изометрияда эллипстің үлкен және кіші осьтері ромбтардың диаганальдарына беттесіп келеді. Эллипстің үлкен осінің бұрмалану көрсеткіші изометрия үшін 1.22-ге тең болса, диметрия үшін 1.06-ға тең. Ал кіші осінің бұрмалану көрсеткіші изометрия үшін 0.54-ке, ал диметрия үшін 0.33-ке тең болады.
50 және 51-суреттерде қоңыр жазықтықтағы эллипс шеңбердің үстінен қарағандағы горизонталь проекция жазықтығындағы көрінісі берілді. Жасыл жазықтықтағы эллипс - шеңбердің оң жағынан қарағандағы көрінісі. Ал сары жазықтықтағы көрініс - шеңбердің алдынан қарағандағы фронталь проекция жа-зықтығындағы көрінісі.
Егер сызбада горизонталь проекция жазықтығында қисық сызықтар мен шеңберлер шамадан тыс көбейіп кетсе, онда нәрсенің аксонометриясын салу үшін қиғаш бұрышты горизон-таль изометрия проекциясын пайдаланады (52-сурет).
және 
координаталар жазықтығына параллель орна-ласады. Бұл дегеніміз 
аксонометриялық осьтердегі бұрмалану көрсет-кіштері 1-ге тең, ал араларын-дағы бұрыштары 900 градус болады, яғни нәрсенің горизонталь проекция жазық-тығындағы проекциясы бұрма-ланбай сол күйінде кескінделеді. Ал 
пен 
аксонометриялық осьтерінің арасындағы бұрыштық шама 1200 градус болады. Кей жағдайда бұл бұрыш 1350 немесе 1500 градус шамасында беріледі.
Изометриялық және диметриялық осьтер бойында шеңбердің аксонометриялық проекциясы эллипстің әр түрлі жағдайда болатынын жоғарыда көрсеттік. Енді төмендегі 53-суретте шеңбердің изометриялық проекциясын циркульдің көмегімен салу жолын көрсетеміз. Эллипсті салу үшін х және у осьтерін жүргізіп, О нүктесін анықтап аламыз. Осы О нүктесі арқылы радиусы R болатын шеңберді сызамыз. Бұл шеңбер х және у осьтерін төрт нүктеде қиып өтеді. Осы қиып өткен нүктелер арқылы х және у осьтеріне параллель сәулелер жүргізіп, 53-суретте көрсетілгендей ромб жүргіземіз. Ромбтың қысыңқы жағымен шеңбердің қиылысқан 1 және 2 нүктелері арқылы радиусы R1 болатын шеңбер доғала-рын сызамыз. Осы доға-лар мен шеңбер осьтері 3 және 4 нүктелерінде қиылысады. Қиылысқан нүктелер арқылы ра-диусы R2 болатын шеңбер сызамыз. Бұл шеңбер шеңбердің ось-терін 5 және 6 нүктелерінде қиып өтеді. Осы нүктелер арқылы радиусы R3 болатын шеңбер жүргіземіз. Екі шеңбердің түйіндесу нүктесін табу үшін, радиусы R1 болатын шеңберлердің 1 және 2 орталары мен радиусы R3 болатын шеңберлердің 5 және 6 орталарын өзара қоссақ, онда бұл сызық шеңбер доғасын 7, 8, 9 және 10 нүктелерінде қиып өтеді. 
Шеңбердің диметриялық проекциясын циркульдің көмегімен салу жолын қарастырайық (54-сурет). Ол үшін алдымен х және у осьтерін жүргізіп, О нүктесін анықтап аламыз. Бұл О нүктесі арқылы радиусы R болатын шеңберді сызамыз. Шеңбер х және у осьтерін төрт нүктеде қиып өтеді. Осы қиып өткен нүктелер арқылы х және у осьтеріне параллель сәулелер жүргізіп, ромб саламыз. О нүктесінен вертикаль түзу жүргізіп, оның бойына эллипстің үлкен осіне тең болатын кесіндіні өлшеп салып, 1 және 2 нүктелерін анықтаймыз. Бұл табылған нүктелер радиусы R1 болатын шеңбер доғаларының ортасы болып табылады. Ромбтың қиылысқан 6 және 8 нүктелері арқылы радиусы R1 шеңбер доғаларын сызамыз. Осы доғалар мен шеңбер осьтері 3 және 4 нүктелерінде қиылысады. Қиылысқан нүктелер арқылы радиусы R2 болатын шеңбер жүргіземіз. Бұл шеңбер радиусы R1 болатын шеңберді 5, 6, 7 және 8-нүктелерінде қиып өтеді. Егер табылған шеңберлер доғаларын өзара қоссақ, онда шеңбердің диметриялық кескіні эллипсті табамыз.
радиустарын өлшеп алып 5, 6, 7 және 8 нүктелерін салып, ромбыны тұрғызамыз. Осы табылған нүктелерден ромбтың қырла-рына тікбұрыш түзулерін жүргіземіз (55-сурет). Бұл түзулер ромбтың кіші диагоналын 1 және 2 нүктесінде қиып өтсе, үлкен диагональ сызығын 3 және 4 нүктелерінде қияды. 1 және 2 нүктелері арқылы радиусы R1 болатын шеңбер доғасын сызамыз. Осы сияқты 3 және 4 нүктелері арқылы радиусы R2 болатын шеңбер доғасын сызамыз. Сонымен табылған шеңберлер доғаларын өзара қоссақ, онда шеңбердің алдынан қарағандағы диметриялық кескіні эллипсті тұрғызамыз.
Жазықтық дегеніміз - нүктелер мен түзулердің жазық бір беттегі жиынтығы (73-сурет). Жазық-тықтар – барлық геометриялық элементтердің ішіндегі ең маңызды түрі. Жазықтықтар ғылым мен техникада, сәулет және бейнелеу өнерінде, тағы да сол сияқты басқа да әр түрлі салаларда кеңінен қолданылады. Әрине сызба геометрия инженерлердің негізгі пәні болғандықтан, жазықтықтардың теориялық зерттеулеріне үлкен көңіл бөлінеді.Жазықтық - нүктелер мен түзулердің жазық бір беттегі жиынтығы деген тұжырым математика саласынан алғанда, ал геометрия жағынан алғанда жазықтықтың бірнеше анықтамалары бар. Жазықтықтар төменгі бірнеше жағдайларда беріледі:
Егер кеңістіктегі орналасқан жазықтық проекция жазықтықтарына параллель немесе перпендикуляр орналаспаған болса, онда мұндай жазықтық жалпы жағдайда орналасқан жазықтық деп аталады.
Егер жазықтық төбелері П1 горизонталь проекция жазықтығына бірдей ара қашықтықтары орналасқан болса, онда жазықтық көлденең П1 проекция жазықтығына парал-лельорналасқан дербес жағдайдағы жазықтық болады (75-сурет). Кеңістікте орналасқан жазықтық проекция жазықты-ғына параллель орна-ласқандықтан, оның проекция жазықты-ғындағы кескіні нақты шамасымен кескінделеді. Мысал қарастырайық, 75-суретте АВС үшбұ-рышы арқылы беріл-ген жазықтықтың кеңістіктегі кескіні көрсетілген. Бұл жазықтық П1 фронталь проекция жазықтығына параллель орналасқан, себебі П1 проекция жазықтығындағы жазықтықтың А1В1С1 проекциясы кеңістікте орналасқан АВС үшбұрышына параллель және проекция жазықтығы мен кеңістіктегі жазықтықтың аралары өзара тең.
Ал 76-суретте кеңістікте орналасқан АВС үшбұрышы арқылы берілген жазықтықтың эпюрасы көрсетілген. Сары П1 горизонталь проекция жазықтық-тығында АВС үшбұрышы арқылы берілген жазықтықтың проекциясы мен көк П2 фронталь проекция жазықтық-тығында АВС үшбұрышы арқылы берілген жазықтықтың проекциясы түзу сызық ретінде берілген.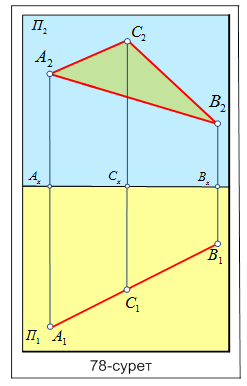
78-суретте кеңістікте орналасқан перпендикуляр АВС жазықтығының сары П1 горизонталь және көк П2 проекция жазықтық-тарындағы кескіндері (проекциялары) көрсетілген.
Жазықтықтың ізі деп кеңістікте орналасқан жазықтықтың проекция жазықтықтармен қиылысу сызығын айтады. Кеңістікте жазықтықтар жалпы жағдайда немесе дербес (ерекше) жағдайда жалпы жағдайда орналасқан Р жазықтығы орналасады. Осы орналасуларына байланысты проекция жазықтықтарында үш немесе екі ізі болады.