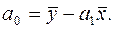|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Регрессионный метод анализа взаимосвязей. Методика построения однофакторной регрессионной модели связи
Регрессионный анализ ставит своей целью получение уравнениязависимости между фактором х и результатом у, по заданным исходным данным. х1 у1 х2 у2 • • • • • • хn уn
Разброс фактических значений yi вокруг теоретических значений
называемые остаточными величинами (или остатками), оценивают отклонения расчетных значений Следовательно, при построении регрессионной модели численные значения коэффициентов ak выбранного типового уравнения регрессии (8) необходимо искать так, чтобы обеспечить наименьшие возможные остатки Для этой цели используется метод наименьших квадратов (МНК), который позволяет рассчитать параметры ak выбранного типового уравнения регрессии таким образом, чтобы теоретическая линия регрессии была бы в среднем наименее удалена от всех точек (xi, yi) по сравнению с любой другой теоретической линией регрессии, отвечающей выбранному типу функции связи (8). Согласно МНК, задача поиска значений параметров ak, минимизирующих сумму погрешностей (16), имеет вид
и решается как задача на экстремум - путем приравнивания нулю первых частных производных функции S по каждому искомому параметру ak уравнения регрессии. Это приводит к системе уравнений, называемой нормальной, решение которой дает численные значения параметров ak, минимизирующие функцию S. Таким образом, параметры связи ak, в силу их расчета по МНК, являются усредненными по всей совокупности наблюдений (xi, yi). Они отражают взаимосвязь признаков X и Y только в общем итоге, по всей совокупности в целом (для каждой индивидуальной пары (xi, yi) значения ak остаются неизвестными). Вследствие усреднения параметров связи ak результативные значения будучи схожими по своей форме на уравнения функциональной зависимости (справедливые для каждого отдельного i-ого наблюдения), они имеют другой содержательный смысл – показывают типичное для всей совокупности в целом соотношение между величинами факторного и результативного признаков. Простейшей формой корреляционной связи признаков является парная линейная корреляция, представляющая собой линейную зависимость результативного признака Y от факторного признака Х. Ее практическое значение состоит в том, что при исследовании взаимосвязи социально-экономических явлений во многих случаях среди всех факторов, влияющих на результативный признак, выделяют один важнейший фактор, который в основном определяет вариацию результативного признака. Уравнение парной линейной корреляционной связи имеет следующий вид:
где а0 - среднее значение признака Y в точке x=0; а0, а1 - коэффициенты уравнения регрессии (параметры связи). Гипотеза о линейной зависимости между признаками Х и Y выдвигается в том случае, если значения обоих признаков возрастают (или убывают) одинаково, примерно в арифметической прогрессии. Уравнение парной линейной корреляции показывает среднее изменение результативного признака Y при изменении фактора Х на однуединицу его измерения, т.е. вариацию признака Y, которая приходится на единицу вариации фактора Х. Знак параметра указывает направление этого изменения. Коэффициенты уравнения а0, а1отыскиваются методом наименьших квадратов (МНК). В основу МНК положено требование минимальности сумм квадратов отклонений эмпирических значений yi от выровненных
Для нахождения значений параметров а0, а1, при которых функция двух переменных Sможет достигнуть минимума, приравнивают к нулю частные производные Sпо а0, а1 и тем самым получают систему 2-х уравнений с двумя неизвестными а0, а1:
Сократив каждое уравнение на –2, раскрыв скобки и перенеся члены с х в одну строку, а с y – в другую, для определения а0, а1 получают систему:
Эта система называется системой нормальных уравнений МНК для линейного уравнения регрессии. Все суммы, необходимые для конкретизации нормальных уравнений, определяют по эмпирическим данным (xi, yi). Решая полученную систему, находят искомые параметры а0, а1 – коэффициенты линейного уравнения регрессии. Расчет коэффициента может быть выполнен по формулам:
Иногда эти коэффициенты удобнее вычислять по формулам:
Построив линейное уравнение регрессии, следует проанализировать качество синтезированной регрессионной модели, оценить адекватность и практическую пригодность модели, дать ее экономическую интерпретации.
Если в качестве модели используется квадратический полином, то МНК дает возможность получить систему из 3-х уравнений с 3-мя неизвестными. Каждый тип модели связи f(x) имеет систему нормальных уравнений, получаемая методом наименьших квадратических (мнк).
Поиск по сайту: |
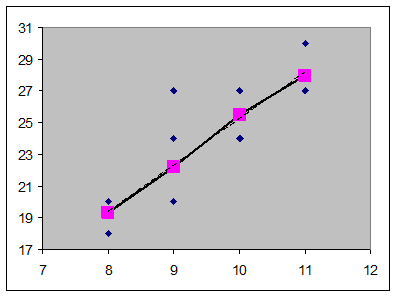

 , рассчитанных по избранному для моделирования уравнению регрессии, обусловлен влиянием множества случайных факторов. Разности
, рассчитанных по избранному для моделирования уравнению регрессии, обусловлен влиянием множества случайных факторов. Разности (16)
(16)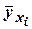 от фактических значений yi.
от фактических значений yi. для всех случаев наблюдения (xi, yi).
для всех случаев наблюдения (xi, yi).
 min (17)
min (17)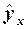 также являются усредненными по всей совокупности наблюдений, откуда вытекает важная особенность уравнений регрессии:
также являются усредненными по всей совокупности наблюдений, откуда вытекает важная особенность уравнений регрессии: ,
,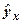 - расчетное теоретическое значение результативного признака Y, полученное по уравнению регрессии;
- расчетное теоретическое значение результативного признака Y, полученное по уравнению регрессии; . При линейной зависимости критерий минимизации (17) принимает вид:
. При линейной зависимости критерий минимизации (17) принимает вид: (18)
(18)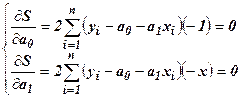
 (19)
(19) ;
;  .
.