 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Формы выражения связей
Корреляционные взаимосвязи признаков имеют разную форму выражения, различаясь по степени тесноты, направлению, количеству факторов в модели связи (рис. 1). Теснота корреляционной связи характеризует степень ее приближения к функциональной связи. Если значению xi признака Х соответствуют близкие друг другу, тесно расположенные около своей средней Таким образом, степень тесноты связи зависит от степени варьирования результативного признака Y при фиксированном значении факторного признака Х. В зависимости от направления изменения результативного признака различаются прямые и обратные связи. Если результативный признак Y изменяется в том же направлении, что и факторный признак Х (т.е. с ростом Х признак Y также возрастает, а при уменьшении Х - уменьшается), то связь прямая. Если же результативный признак меняется в противоположном направлении, то связь обратная. По количеству факторов, действующих на результативный признак, различают связи однофакторные и многофакторные. Если исследуется связь между одним признаком-фактором Х и результативным признаком Y (при абстрагировании от влияния на Y всех других факторов), то говорят об однофакторной связи и парной корреляции (рассматривается пара признаков). Если же изучается воздействие на Y нескольких факторных признаков X1,X2, … , Xm, то связь называют многофакторной, а корреляцию множественной. В случае многофакторной связи имеется ввиду, что все влияющие факторы действуют в комплексе – одновременно и во взаимосвязи. Если же изучается зависимость между результативным и одним из факторных признаков при фиксированных значениях других факторных признаков, то говорят о частной корреляции. По форме связи различают линейные и нелинейные модели связи. В однофакторных регрессионных моделях взаимосвязи социально-экономических явлений наиболее часто используются следующие типы математических функций, описывающих теоретическую линию регрессии и характеризующих механизм взаимодействия факторного и результативного признаков:
Коэффициенты уравнений регрессии a0, a1, a2, … называют параметрами связи.
Поиск по сайту: |
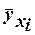 значения yi1, yi2, …, yik, то связь тесная (сильная). Если же эти результативные значения существенно отклоняются от
значения yi1, yi2, …, yik, то связь тесная (сильная). Если же эти результативные значения существенно отклоняются от 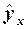 = a0 + a1x - линейная,
= a0 + a1x - линейная, - гиперболическая, (8)
- гиперболическая, (8)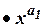 - степенная,
- степенная,  - показательная.
- показательная.