|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Численные методы решения задачи Коши для ОДУ первого порядкаСтр 1 из 2Следующая ⇒
Постановка задачи. Найти решение ОДУ первого порядка При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом Целью является построение таблицы
т.е. ищутся приближенные значения y в узлах сетки. Интегрируя уравнение на отрезке Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка то получим явную формулу Эйлера: Порядок расчетов: Зная Геометрическая интерпретация метода Эйлера: Пользуясь тем, что в точке x0 известно решение y(x0) = y0 и значение его производной
Явный метод Эйлера имеет первый порядок точности или аппроксимации. Если использовать формулу правых прямоугольников: Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения Неявный метод Эйлера имеет первый порядок точности или аппроксимации. Модифицированный метод Эйлера: в данном методе вычисление Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности. Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(xi+1) по формуле вида где ……………………………………………. Здесь an, bnj, pn, При построения методов Рунге–Кутты параметры функции Схема Рунге – Кутта четвертого порядка точности: Пример. Решить задачу Коши: Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта. Точное решение: Расчетные формулы по явному методу Эйлера для данного примера: Расчетные формулы модифицированного метода Эйлера: Расчетные формулы метода Рунге – Кутта:
y1 – метод Эйлера, y2 – модифицированный метод Эйлера, y3 – метод Рунге Кутта. Видно, что самым точным является метод Рунге – Кутта.
Поиск по сайту: |
 на отрезке
на отрезке 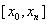 при условии
при условии 
 , расчетными узлами служат точки
, расчетными узлами служат точки  промежутка [x0, xn].
промежутка [x0, xn]. , получим
, получим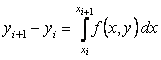
 ,
, ,
,  .
. , находим
, находим  , затем
, затем  т.д.
т.д. , можно записать уравнение касательной к графику искомой функции
, можно записать уравнение касательной к графику искомой функции  в точке
в точке  :
:  . При достаточно малом шаге h ордината
. При достаточно малом шаге h ордината  этой касательной, полученная подстановкой в правую часть значения
этой касательной, полученная подстановкой в правую часть значения  , должна мало отличаться от ординаты y(x1) решенияy(x) задачи Коши. Следовательно, точка
, должна мало отличаться от ординаты y(x1) решенияy(x) задачи Коши. Следовательно, точка  пересечения касательной с прямой x = x1 может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую
пересечения касательной с прямой x = x1 может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую 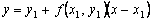 , которая приближенно отражает поведение касательной к
, которая приближенно отражает поведение касательной к  . Подставляя сюда
. Подставляя сюда  (т.е. пересечение с прямой x = x2), получим приближенное значение y(x) в точке x2:
(т.е. пересечение с прямой x = x2), получим приближенное значение y(x) в точке x2:  и т.д. В итоге для i–й точки получим формулу Эйлера.
и т.д. В итоге для i–й точки получим формулу Эйлера.
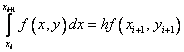 , то придем к методу
, то придем к методу ,
,  по известному значению
по известному значению  требуется решать уравнение, в общем случае нелинейное.
требуется решать уравнение, в общем случае нелинейное. состоит из двух этапов:
состоит из двух этапов:
 ,
,



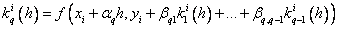 .
. – некоторые фиксированные числа (параметры).
– некоторые фиксированные числа (параметры). (an, bnj, pn) подбирают таким образом, чтобы получить нужный порядок аппроксимации.
(an, bnj, pn) подбирают таким образом, чтобы получить нужный порядок аппроксимации.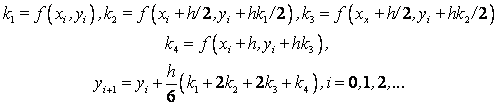
 .
.