|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Условия принадлежности прямой линии плоскости
Способы задания плоскости Плоскость на чертеже может быть задана следующими способами (табл. 5.1). Таблица 5.1
Положение плоскости относительно плоскостей проекций
Плоскости в пространстве могут занимать общее (табл. 5.2) и частное положение (табл. 5.3 и табл. 5.4). Плоскость общего положения Таблица 5.2
Плоскости частного положения Плоскостью частного положения называют плоскость, которая либо перпендикулярна, либо параллельна одной из плоскостей проекций. Плоскости частного положения могут быть проецирующими (табл. 5.3) и плоскостями уровня (табл. 5.4). Таблица 5.3 Плоскости проецирующие
Таким образом, если плоскость перпендикулярна одной из плоскостей проекций, то на эту плоскость она проецируется в виде прямой линии. Задача Построить комплексный чертеж фронтально-, профильно- и горизонтальнопроецирующих плоскостей, если они заданы: а) тремя точками; б) прямой и точкой, не принадлежащей данной прямой; в) двумя пересекающимися прямыми; г) двумя параллельными прямыми. Таблица 5.4 Плоскости уровня
Таким образом, если плоскость параллельна какой-либо плоскости проекций, то на эту плоскость она проецируется в натуральную величину, а две ее другие проекции есть прямые линии параллельные осям проекций. Задача Постройте комплексный чертеж плоскости уровня (горизонтальной, фронтальной, профильной), если они заданы: а) тремя точками; б) прямой и точкой, не лежащей на прямой; в) двумя пересекающимися прямыми; г) двумя параллельными прямыми; д) плоской фигурой. Условия принадлежности прямой линии плоскости Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие этой плоскости или через одну точку этой плоскости, параллельно прямой, лежащей в этой плоскости.
Поиск по сайту: |


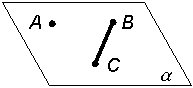







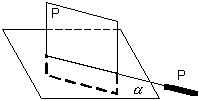



 (D ABC)^ p1. Любой элемент, лежащий в этой плоскости, проецируется на плоскость p1 в прямую линию; горизонтальная проекция D A1B1C1 есть прямая линия на плоскости p1; угол b есть угол наклона этой плоскости к плоскостям p2. Он проецируется на горизонтальную плоскость без искажения
(D ABC)^ p1. Любой элемент, лежащий в этой плоскости, проецируется на плоскость p1 в прямую линию; горизонтальная проекция D A1B1C1 есть прямая линия на плоскости p1; угол b есть угол наклона этой плоскости к плоскостям p2. Он проецируется на горизонтальную плоскость без искажения